Question Number 49148 by mr W last updated on 03/Dec/18
Commented by mr W last updated on 04/Dec/18

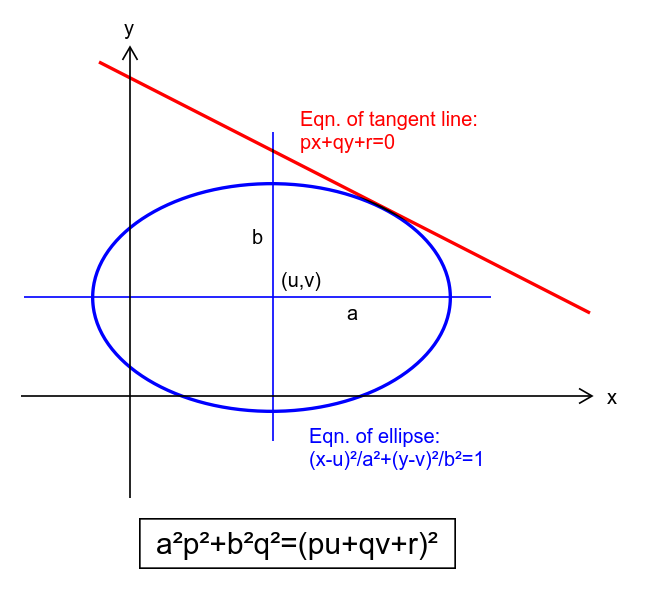
$${This}\:{is}\:{not}\:{a}\:{question},\:{but}\:{an}\:{useful} \\ $$$${information}. \\ $$$$ \\ $$$${Maybe}\:{someone}\:{has}\:{delight}\:{to}\:{prove}\:{it}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Dec/18

$${thank}\:{you}\:{sir}… \\ $$
Answered by ajfour last updated on 04/Dec/18
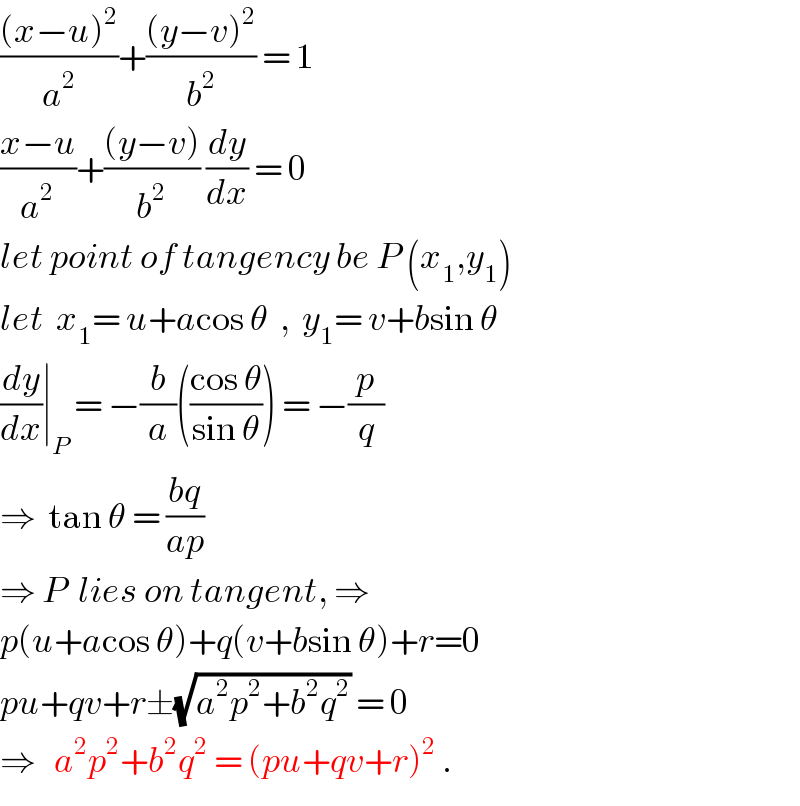
$$\frac{\left({x}−{u}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}−{v}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$$\frac{{x}−{u}}{{a}^{\mathrm{2}} }+\frac{\left({y}−{v}\right)}{{b}^{\mathrm{2}} }\:\frac{{dy}}{{dx}}\:=\:\mathrm{0} \\ $$$${let}\:{point}\:{of}\:{tangency}\:{be}\:{P}\:\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right) \\ $$$${let}\:\:{x}_{\mathrm{1}} =\:{u}+{a}\mathrm{cos}\:\theta\:\:,\:\:{y}_{\mathrm{1}} =\:{v}+{b}\mathrm{sin}\:\theta \\ $$$$\frac{{dy}}{{dx}}\mid_{{P}} \:=\:−\frac{{b}}{{a}}\left(\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}\right)\:=\:−\frac{{p}}{{q}} \\ $$$$\Rightarrow\:\:\mathrm{tan}\:\theta\:=\:\frac{{bq}}{{ap}} \\ $$$$\Rightarrow\:{P}\:\:{lies}\:{on}\:{tangent},\:\Rightarrow \\ $$$${p}\left({u}+{a}\mathrm{cos}\:\theta\right)+{q}\left({v}+{b}\mathrm{sin}\:\theta\right)+{r}=\mathrm{0} \\ $$$${pu}+{qv}+{r}\pm\sqrt{{a}^{\mathrm{2}} {p}^{\mathrm{2}} +{b}^{\mathrm{2}} {q}^{\mathrm{2}} }\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\:{a}^{\mathrm{2}} {p}^{\mathrm{2}} +{b}^{\mathrm{2}} {q}^{\mathrm{2}} \:=\:\left({pu}+{qv}+{r}\right)^{\mathrm{2}} \:. \\ $$
Commented by mr W last updated on 04/Dec/18

$${thank}\:{you}\:{for}\:{the}\:{proof}\:{sir}! \\ $$$${this}\:{result}\:{is}\:{very}\:{helpful}\:{in}\:{solving} \\ $$$${many}\:{questions}\:{relating}\:{to}\:{ellipse}. \\ $$
