Question Number 49252 by cesar.marval.larez@gmail.com last updated on 04/Dec/18
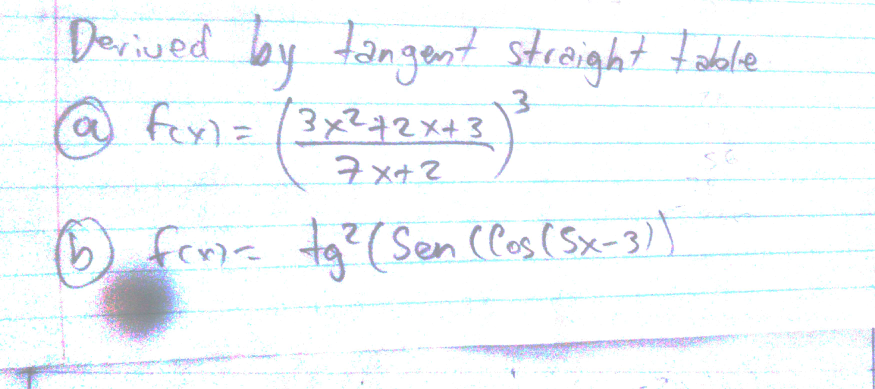
Answered by kaivan.ahmadi last updated on 05/Dec/18
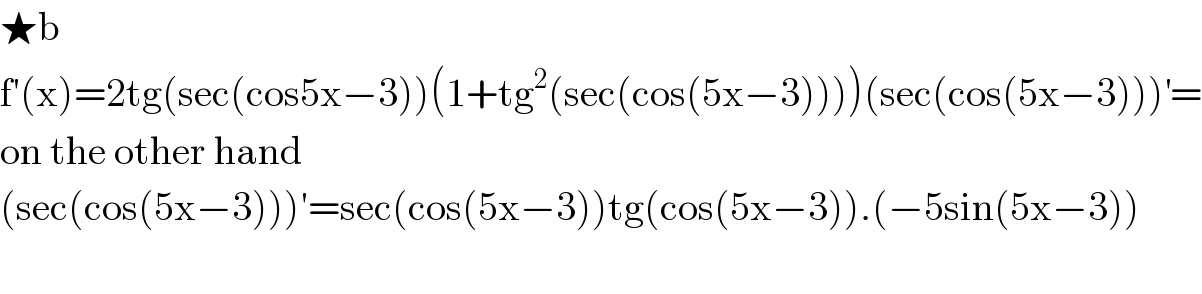
$$\bigstar\mathrm{b} \\ $$$$\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{2tg}\left(\mathrm{sec}\left(\mathrm{cos5x}−\mathrm{3}\right)\right)\left(\mathrm{1}+\mathrm{tg}^{\mathrm{2}} \left(\mathrm{sec}\left(\mathrm{cos}\left(\mathrm{5x}−\mathrm{3}\right)\right)\right)\right)\left(\mathrm{sec}\left(\mathrm{cos}\left(\mathrm{5x}−\mathrm{3}\right)\right)\right)^{'} = \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hand} \\ $$$$\left(\mathrm{sec}\left(\mathrm{cos}\left(\mathrm{5x}−\mathrm{3}\right)\right)\right)'=\mathrm{sec}\left(\mathrm{cos}\left(\mathrm{5x}−\mathrm{3}\right)\right)\mathrm{tg}\left(\mathrm{cos}\left(\mathrm{5x}−\mathrm{3}\right)\right).\left(−\mathrm{5sin}\left(\mathrm{5x}−\mathrm{3}\right)\right) \\ $$$$ \\ $$
