Question Number 49283 by Pk1167156@gmail.com last updated on 05/Dec/18
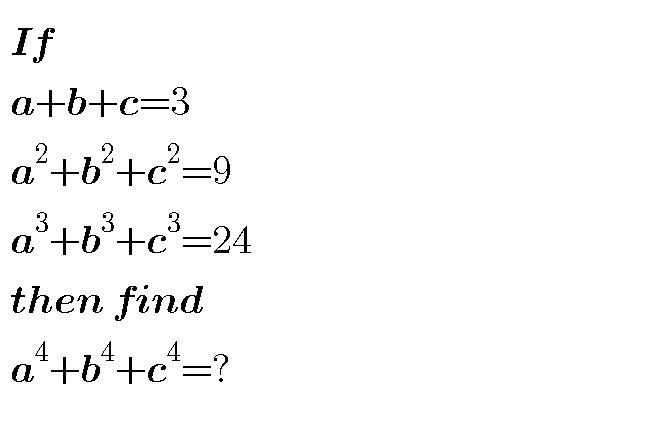
Answered by afachri last updated on 05/Dec/18
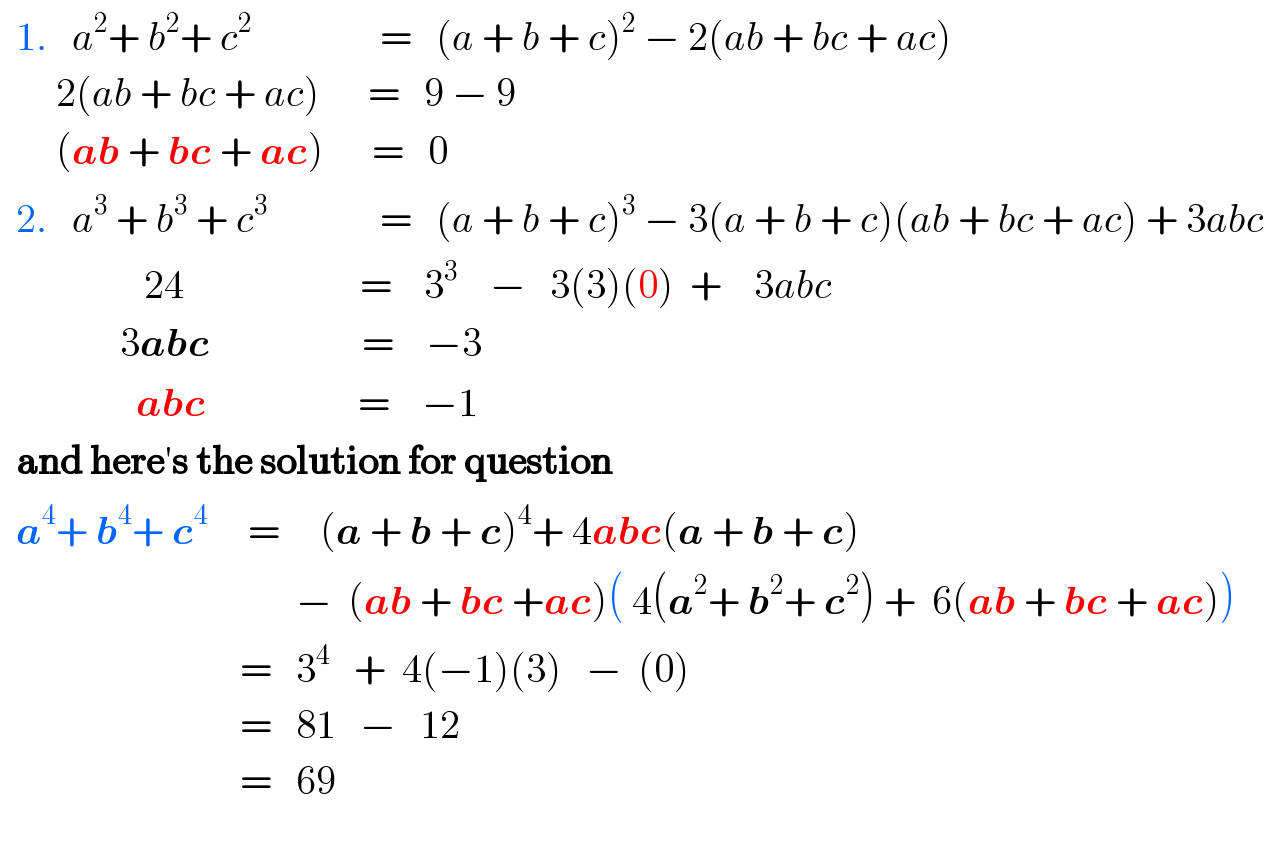
$$\:\:\mathrm{1}.\:\:\:{a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} +\:{c}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\:\left({a}\:+\:{b}\:+\:{c}\right)^{\mathrm{2}} \:−\:\mathrm{2}\left({ab}\:+\:{bc}\:+\:{ac}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{2}\left({ab}\:+\:{bc}\:+\:{ac}\right)\:\:\:\:\:\:=\:\:\:\mathrm{9}\:−\:\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\left(\boldsymbol{{ab}}\:+\:\boldsymbol{{bc}}\:+\:\boldsymbol{{ac}}\right)\:\:\:\:\:\:=\:\:\:\mathrm{0} \\ $$$$\:\:\mathrm{2}.\:\:\:{a}^{\mathrm{3}} \:+\:{b}^{\mathrm{3}} \:+\:{c}^{\mathrm{3}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\:\left({a}\:+\:{b}\:+\:{c}\right)^{\mathrm{3}} \:−\:\mathrm{3}\left({a}\:+\:{b}\:+\:{c}\right)\left({ab}\:+\:{bc}\:+\:{ac}\right)\:+\:\mathrm{3}{abc} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{24}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\:\:\mathrm{3}^{\mathrm{3}} \:\:\:\:−\:\:\:\mathrm{3}\left(\mathrm{3}\right)\left(\mathrm{0}\right)\:\:+\:\:\:\:\mathrm{3}{abc}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}\boldsymbol{{abc}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\:\:−\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{abc}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\:\:−\mathrm{1} \\ $$$$\:\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{here}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{solution}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{question}} \\ $$$$\:\:\boldsymbol{{a}}^{\mathrm{4}} +\:\boldsymbol{{b}}^{\mathrm{4}} +\:\boldsymbol{{c}}^{\mathrm{4}} \:\:\:\:\:=\:\:\:\:\:\left(\boldsymbol{{a}}\:+\:\boldsymbol{{b}}\:+\:\boldsymbol{{c}}\right)^{\mathrm{4}} +\:\mathrm{4}\boldsymbol{{abc}}\left(\boldsymbol{{a}}\:+\:\boldsymbol{{b}}\:+\:\boldsymbol{{c}}\right)\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\left(\boldsymbol{{ab}}\:+\:\boldsymbol{{bc}}\:+\boldsymbol{{ac}}\right)\left(\:\mathrm{4}\left(\boldsymbol{{a}}^{\mathrm{2}} +\:\boldsymbol{{b}}^{\mathrm{2}} +\:\boldsymbol{{c}}^{\mathrm{2}} \right)\:+\:\:\mathrm{6}\left(\boldsymbol{{ab}}\:+\:\boldsymbol{{bc}}\:+\:\boldsymbol{{ac}}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\:\mathrm{3}^{\mathrm{4}} \:\:\:+\:\:\mathrm{4}\left(−\mathrm{1}\right)\left(\mathrm{3}\right)\:\:\:−\:\:\left(\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\:\mathrm{81}\:\:\:−\:\:\:\mathrm{12} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\:\mathrm{69} \\ $$$$ \\ $$
Commented by Pk1167156@gmail.com last updated on 05/Dec/18
Thank you very much sir
Commented by afachri last updated on 05/Dec/18

$$\mathrm{ur}\:\mathrm{welcome}\:\mathrm{Sir} \\ $$
