Menu Close

Question-49299

Tinku Tara 0 Comments
Pin




Question Number 49299 by peter frank last updated on 05/Dec/18
Commented by maxmathsup by imad last updated on 05/Dec/18
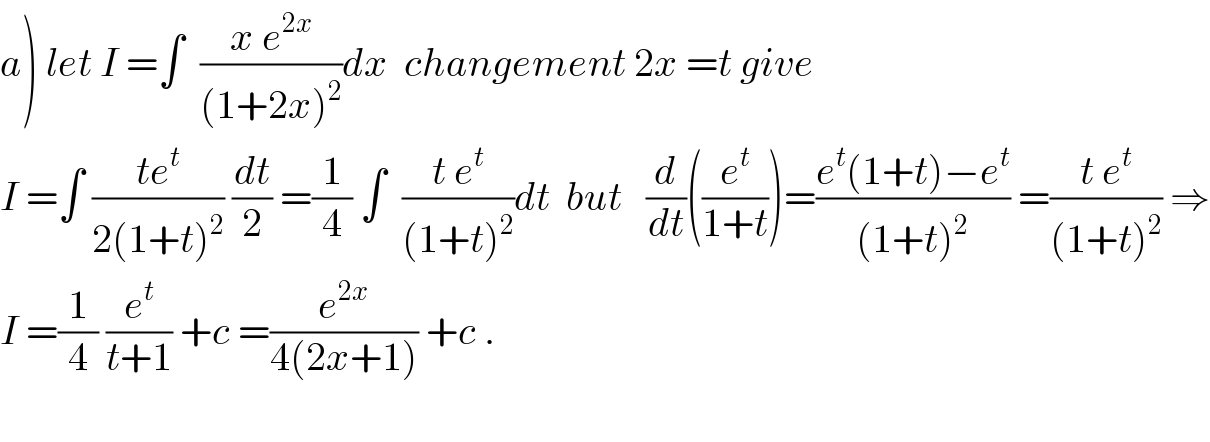
a) let I =∫ ((x e^(2x) )/((1+2x)^2 ))dx changement 2x =t give I =∫ ((te^t )/(2(1+t)^2 )) (dt/2) =(1/4) ∫ ((t e^t )/((1+t)^2 ))dt but (d/dt)((e^t /(1+t)))=((e^t (1+t)−e^t )/((1+t)^2 )) =((t e^t )/((1+t)^2 )) ⇒ I =(1/4) (e^t /(t+1)) +c =(e^(2x) /(4(2x+1))) +c .
$$\left.{a}\right)\:{let}\:{I}\:=\int\:\:\frac{{x}\:{e}^{\mathrm{2}{x}} }{\left(\mathrm{1}+\mathrm{2}{x}\right)^{\mathrm{2}} }{dx}\:\:{changement}\:\mathrm{2}{x}\:={t}\:{give} \\ $$$${I}\:=\int\:\frac{{te}^{{t}} }{\mathrm{2}\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\:\frac{{dt}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\:\frac{{t}\:{e}^{{t}} }{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt}\:\:{but}\:\:\:\frac{{d}}{{dt}}\left(\frac{{e}^{{t}} }{\mathrm{1}+{t}}\right)=\frac{{e}^{{t}} \left(\mathrm{1}+{t}\right)−{e}^{{t}} }{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\:=\frac{{t}\:{e}^{{t}} }{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{{e}^{{t}} }{{t}+\mathrm{1}}\:+{c}\:=\frac{{e}^{\mathrm{2}{x}} }{\mathrm{4}\left(\mathrm{2}{x}+\mathrm{1}\right)}\:+{c}\:. \\ $$$$ \\ $$
Commented by Abdo msup. last updated on 05/Dec/18
b) let A =∫_1 ^2 (dx/(x^2 (√(5x^2 −1)))) ⇒A =(1/( (√5)))∫_1 ^2 (dx/(x^2 (√(x^2 −(1/5))))) =_(x =(1/( (√5)))ch(t)) (1/(5(√5))) ∫_(argch((√5))) ^(argch(2(√5))) ((sh(t)dt)/((1/5)ch^2 tsh(t))) =(1/( (√5))) ∫_(ln((√5)+2)) ^(ln(2(√5)+(√(19)))) ((2dt)/(1+ch(2t))) =(2/( (√5))) ∫_(ln(2+(√5))) ^(ln((√(19)) +2(√5){) (dt/(1+((e^(2t) +e^(−2t) )/2))) =(4/( (√5))) ∫_(ln(2+(√5))) ^(ln((√(19)) +2(√5))) (dt/(2 +e^(2t) +e^(−2t) )) =_(e^(2t) =u) (4/( (√5))) ∫_((2+(√5))^2 ) ^(((√(19))+2(√5))^2 ) (du/(2(2 +u +u^(−1) )u)) =(2/( (√5))) ∫_((2+(√5))^2 ) ^(((√(19)) +2(√5))^2 ) (du/(2u +u^2 +1)) =(2/( (√5))) ∫_((2+(√5))^2 ) ^(((√(19))+2(√5))^2 ) (du/((u+1)^2 )) =(2/( (√5)))[−(1/(1+u))]_((2+(√5))^2 ) ^(((√(19))+2(√5))^2 ) =(2/( (√5))){ (1/(1+(2+(√5))^2 )) −(1/(1+((√(19))+2(√5))^2 ))} . =
$$\left.{b}\right)\:{let}\:{A}\:=\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{1}}}\:\Rightarrow{A}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{5}}}} \\ $$$$=_{{x}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}{ch}\left({t}\right)} \:\:\:\frac{\mathrm{1}}{\mathrm{5}\sqrt{\mathrm{5}}}\:\int_{{argch}\left(\sqrt{\mathrm{5}}\right)} ^{{argch}\left(\mathrm{2}\sqrt{\mathrm{5}}\right)} \:\:\:\:\:\frac{{sh}\left({t}\right){dt}}{\frac{\mathrm{1}}{\mathrm{5}}{ch}^{\mathrm{2}} {tsh}\left({t}\right)} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\:\int_{{ln}\left(\sqrt{\mathrm{5}}+\mathrm{2}\right)} ^{{ln}\left(\mathrm{2}\sqrt{\mathrm{5}}+\sqrt{\mathrm{19}}\right)} \:\frac{\mathrm{2}{dt}}{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\int_{{ln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)} ^{{ln}\left(\sqrt{\mathrm{19}}\:+\mathrm{2}\sqrt{\mathrm{5}}\left\{\right.\right.} \:\:\:\frac{{dt}}{\mathrm{1}+\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}} \\ $$$$=\frac{\mathrm{4}}{\:\sqrt{\mathrm{5}}}\:\int_{{ln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)} ^{{ln}\left(\sqrt{\mathrm{19}}\:+\mathrm{2}\sqrt{\mathrm{5}}\right)} \:\:\:\:\frac{{dt}}{\mathrm{2}\:+{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} } \\ $$$$=_{{e}^{\mathrm{2}{t}} ={u}} \:\:\frac{\mathrm{4}}{\:\sqrt{\mathrm{5}}}\:\:\int_{\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} } ^{\left(\sqrt{\mathrm{19}}+\mathrm{2}\sqrt{\mathrm{5}}\right)^{\mathrm{2}} } \:\:\:\:\:\:\frac{{du}}{\mathrm{2}\left(\mathrm{2}\:+{u}\:+{u}^{−\mathrm{1}} \right){u}} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\int_{\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} } ^{\left(\sqrt{\mathrm{19}}\:+\mathrm{2}\sqrt{\mathrm{5}}\right)^{\mathrm{2}} } \:\:\frac{{du}}{\mathrm{2}{u}\:+{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\int_{\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} } ^{\left(\sqrt{\mathrm{19}}+\mathrm{2}\sqrt{\mathrm{5}}\right)^{\mathrm{2}} } \:\:\frac{{du}}{\left({u}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\left[−\frac{\mathrm{1}}{\mathrm{1}+{u}}\right]_{\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} } ^{\left(\sqrt{\mathrm{19}}+\mathrm{2}\sqrt{\mathrm{5}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\left\{\:\:\frac{\mathrm{1}}{\mathrm{1}+\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{1}+\left(\sqrt{\mathrm{19}}+\mathrm{2}\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }\right\}\:. \\ $$$$= \\ $$
Commented by peter frank last updated on 06/Dec/18
thank you sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Dec/18
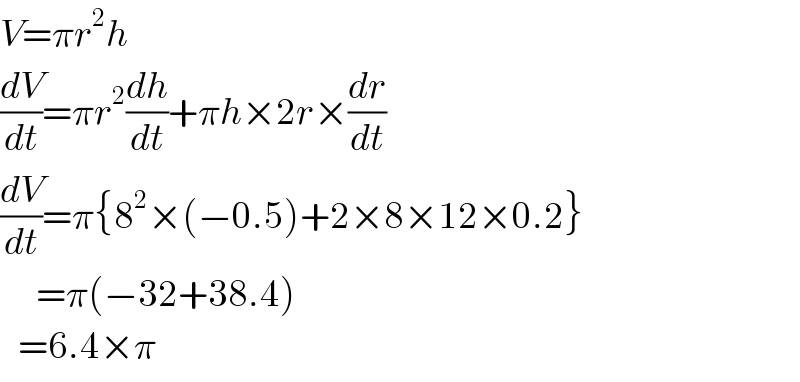
V=πr^2 h (dV/dt)=πr^2 (dh/dt)+πh×2r×(dr/dt) (dV/dt)=π{8^2 ×(−0.5)+2×8×12×0.2} =π(−32+38.4) =6.4×π
$${V}=\pi{r}^{\mathrm{2}} {h} \\ $$$$\frac{{dV}}{{dt}}=\pi{r}^{\mathrm{2}} \frac{{dh}}{{dt}}+\pi{h}×\mathrm{2}{r}×\frac{{dr}}{{dt}} \\ $$$$\frac{{dV}}{{dt}}=\pi\left\{\mathrm{8}^{\mathrm{2}} ×\left(−\mathrm{0}.\mathrm{5}\right)+\mathrm{2}×\mathrm{8}×\mathrm{12}×\mathrm{0}.\mathrm{2}\right\} \\ $$$$\:\:\:\:\:\:=\pi\left(−\mathrm{32}+\mathrm{38}.\mathrm{4}\right) \\ $$$$\:\:\:=\mathrm{6}.\mathrm{4}×\pi \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Dec/18
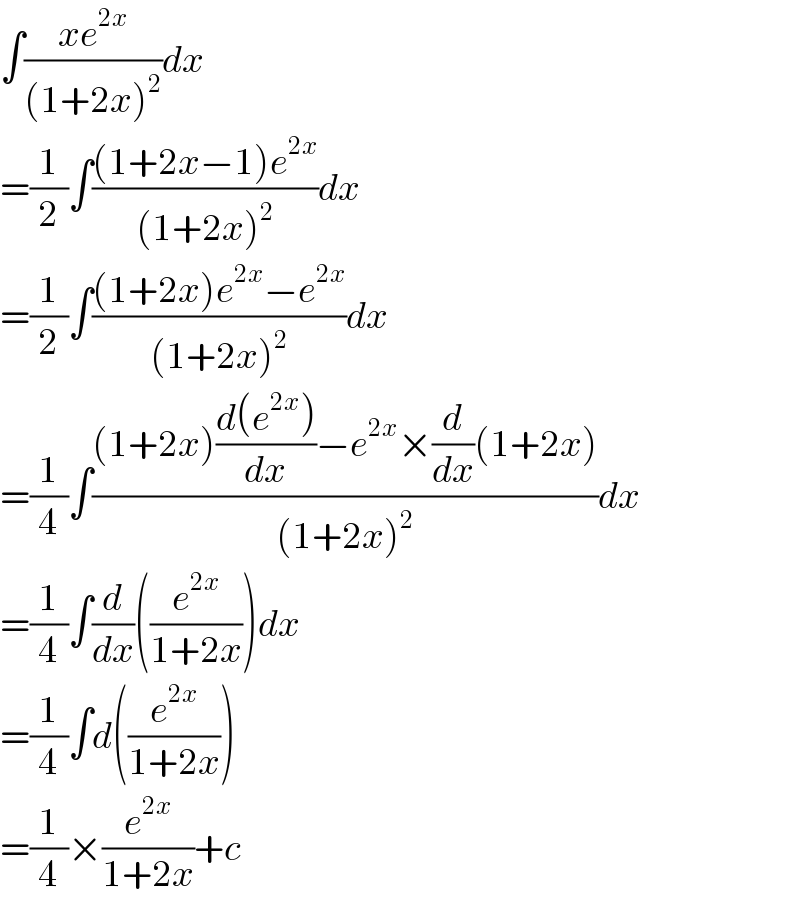
∫((xe^(2x) )/((1+2x)^2 ))dx =(1/2)∫(((1+2x−1)e^(2x) )/((1+2x)^2 ))dx =(1/2)∫(((1+2x)e^(2x) −e^(2x) )/((1+2x)^2 ))dx =(1/4)∫(((1+2x)((d(e^(2x) ))/dx)−e^(2x) ×(d/dx)(1+2x))/((1+2x)^2 ))dx =(1/4)∫(d/dx)((e^(2x) /(1+2x)))dx =(1/4)∫d((e^(2x) /(1+2x))) =(1/4)×(e^(2x) /(1+2x))+c
$$\int\frac{{xe}^{\mathrm{2}{x}} }{\left(\mathrm{1}+\mathrm{2}{x}\right)^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{1}+\mathrm{2}{x}−\mathrm{1}\right){e}^{\mathrm{2}{x}} }{\left(\mathrm{1}+\mathrm{2}{x}\right)^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{1}+\mathrm{2}{x}\right){e}^{\mathrm{2}{x}} −{e}^{\mathrm{2}{x}} }{\left(\mathrm{1}+\mathrm{2}{x}\right)^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\left(\mathrm{1}+\mathrm{2}{x}\right)\frac{{d}\left({e}^{\mathrm{2}{x}} \right)}{{dx}}−{e}^{\mathrm{2}{x}} ×\frac{{d}}{{dx}}\left(\mathrm{1}+\mathrm{2}{x}\right)}{\left(\mathrm{1}+\mathrm{2}{x}\right)^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{d}}{{dx}}\left(\frac{{e}^{\mathrm{2}{x}} }{\mathrm{1}+\mathrm{2}{x}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int{d}\left(\frac{{e}^{\mathrm{2}{x}} }{\mathrm{1}+\mathrm{2}{x}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}×\frac{{e}^{\mathrm{2}{x}} }{\mathrm{1}+\mathrm{2}{x}}+{c} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Dec/18
∫_1 ^2 (dx/(x^2 (√(5x^2 −1)))) I=∫(dx/(x^2 (√(5x^2 −1)))) x=(1/t) dx=((−dt)/t^2 ) ∫((−dt)/(t^2 ×(1/t^(2 ) )×(√(5((1/t))^2 −1)))) ∫((−t×dt)/( (√(5−t^2 )))) (1/2)∫((d(5−t^2 ))/( (√(5−t^2 )))) =(1/2)×(((5−t^2 )^(((−1)/2)+1) )/(((−1)/2)+1))+c =(√(5−t^2 )) +c =(√(5−(1/x^2 ))) +c so answer of resuired intregal is ∣(√(5−(1/x^2 ) )) ∣_1 ^2 =(√(5−(1/4))) −(√(5−(1/1))) =((√(19))/2)−2
$$\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{dx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{1}}} \\ $$$${I}=\int\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{1}}}\:\:{x}=\frac{\mathrm{1}}{{t}}\:\:\:\:{dx}=\frac{−{dt}}{{t}^{\mathrm{2}} } \\ $$$$\int\frac{−{dt}}{{t}^{\mathrm{2}} ×\frac{\mathrm{1}}{{t}^{\mathrm{2}\:} }×\sqrt{\mathrm{5}\left(\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\int\frac{−{t}×{dt}}{\:\sqrt{\mathrm{5}−{t}^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left(\mathrm{5}−{t}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{5}−{t}^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\left(\mathrm{5}−{t}^{\mathrm{2}} \right)^{\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{1}} }{\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{1}}+{c} \\ $$$$=\sqrt{\mathrm{5}−{t}^{\mathrm{2}} }\:+{c} \\ $$$$=\sqrt{\mathrm{5}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:+{c} \\ $$$${so}\:{answer}\:{of}\:{resuired}\:{intregal}\:{is} \\ $$$$\mid\sqrt{\mathrm{5}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:}\:\mid_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$=\sqrt{\mathrm{5}−\frac{\mathrm{1}}{\mathrm{4}}}\:\:−\sqrt{\mathrm{5}−\frac{\mathrm{1}}{\mathrm{1}}}\: \\ $$$$=\frac{\sqrt{\mathrm{19}}}{\mathrm{2}}−\mathrm{2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *