Question Number 49468 by munnabhai455111@gmail.com last updated on 07/Dec/18
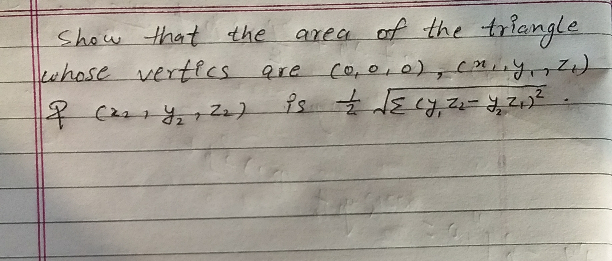
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Dec/18
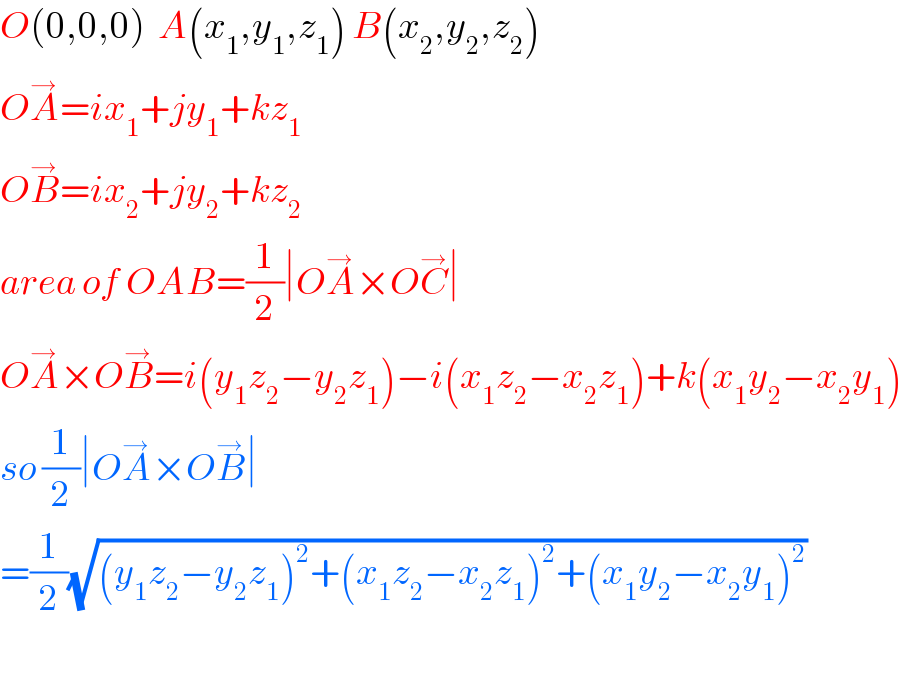
$${O}\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\:\:{A}\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} ,{z}_{\mathrm{1}} \right)\:{B}\left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} ,{z}_{\mathrm{2}} \right) \\ $$$${O}\overset{\rightarrow} {{A}}={ix}_{\mathrm{1}} +{jy}_{\mathrm{1}} +{kz}_{\mathrm{1}} \\ $$$${O}\overset{\rightarrow} {{B}}={ix}_{\mathrm{2}} +{jy}_{\mathrm{2}} +{kz}_{\mathrm{2}} \\ $$$${area}\:{of}\:{OAB}=\frac{\mathrm{1}}{\mathrm{2}}\mid{O}\overset{\rightarrow} {{A}}×{O}\overset{\rightarrow} {{C}}\mid \\ $$$${O}\overset{\rightarrow} {{A}}×{O}\overset{\rightarrow} {{B}}={i}\left({y}_{\mathrm{1}} {z}_{\mathrm{2}} −{y}_{\mathrm{2}} {z}_{\mathrm{1}} \right)−{i}\left({x}_{\mathrm{1}} {z}_{\mathrm{2}} −{x}_{\mathrm{2}} {z}_{\mathrm{1}} \right)+{k}\left({x}_{\mathrm{1}} {y}_{\mathrm{2}} −{x}_{\mathrm{2}} {y}_{\mathrm{1}} \right) \\ $$$${so}\:\frac{\mathrm{1}}{\mathrm{2}}\mid{O}\overset{\rightarrow} {{A}}×{O}\overset{\rightarrow} {{B}}\mid \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\left({y}_{\mathrm{1}} {z}_{\mathrm{2}} −{y}_{\mathrm{2}} {z}_{\mathrm{1}} \right)^{\mathrm{2}} +\left({x}_{\mathrm{1}} {z}_{\mathrm{2}} −{x}_{\mathrm{2}} {z}_{\mathrm{1}} \right)^{\mathrm{2}} +\left({x}_{\mathrm{1}} {y}_{\mathrm{2}} −{x}_{\mathrm{2}} {y}_{\mathrm{1}} \right)^{\mathrm{2}} }\: \\ $$$$ \\ $$
