Question Number 49534 by aseerimad last updated on 07/Dec/18
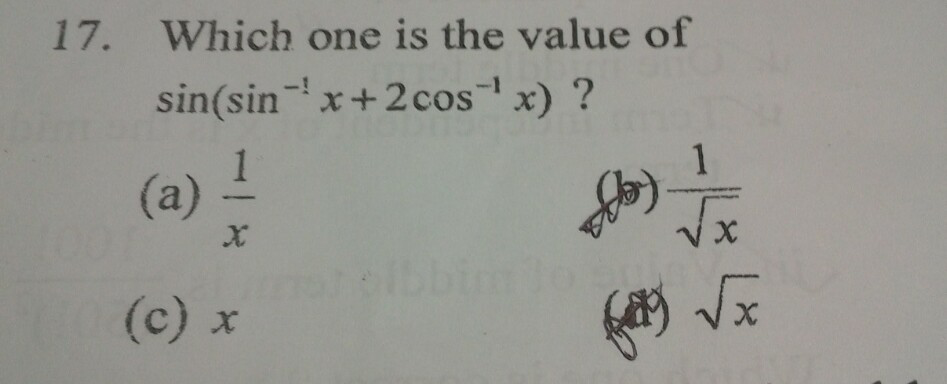
Commented by aseerimad last updated on 07/Dec/18
$${how}\:{is}\:{this}\:{done}\:{in}\:{short}?\:{Thanks}\:{in}\:{advance}. \\ $$
Commented by Abdo msup. last updated on 08/Dec/18
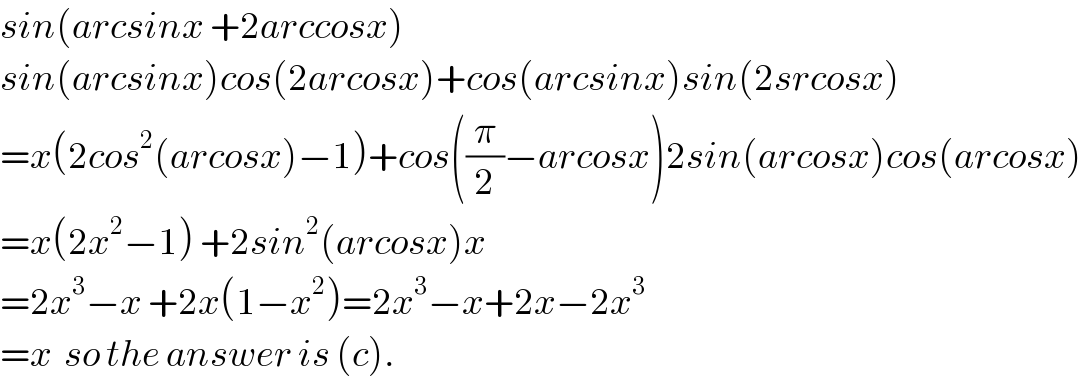
$${sin}\left({arcsinx}\:+\mathrm{2}{arccosx}\right) \\ $$$${sin}\left({arcsinx}\right){cos}\left(\mathrm{2}{arcosx}\right)+{cos}\left({arcsinx}\right){sin}\left(\mathrm{2}{srcosx}\right) \\ $$$$={x}\left(\mathrm{2}{cos}^{\mathrm{2}} \left({arcosx}\right)−\mathrm{1}\right)+{cos}\left(\frac{\pi}{\mathrm{2}}−{arcosx}\right)\mathrm{2}{sin}\left({arcosx}\right){cos}\left({arcosx}\right) \\ $$$$={x}\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}\right)\:+\mathrm{2}{sin}^{\mathrm{2}} \left({arcosx}\right){x} \\ $$$$=\mathrm{2}{x}^{\mathrm{3}} −{x}\:+\mathrm{2}{x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)=\mathrm{2}{x}^{\mathrm{3}} −{x}+\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{3}} \\ $$$$={x}\:\:{so}\:{the}\:{answer}\:{is}\:\left({c}\right). \\ $$
Commented by aseerimad last updated on 09/Dec/18

$${thank}\:{you}\:{sir} \\ $$
Answered by behi83417@gmail.com last updated on 07/Dec/18
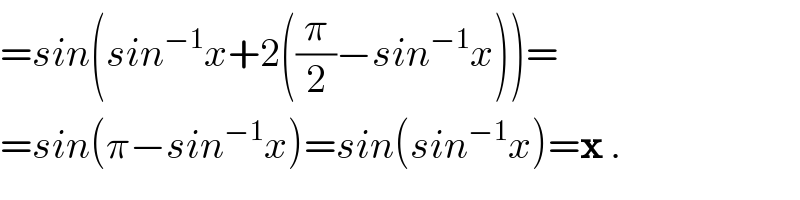
$$={sin}\left({sin}^{−\mathrm{1}} {x}+\mathrm{2}\left(\frac{\pi}{\mathrm{2}}−{sin}^{−\mathrm{1}} {x}\right)\right)= \\ $$$$={sin}\left(\pi−{sin}^{−\mathrm{1}} {x}\right)={sin}\left({sin}^{−\mathrm{1}} {x}\right)=\boldsymbol{\mathrm{x}}\:. \\ $$
Commented by aseerimad last updated on 09/Dec/18

$${thank}\:{you}\:{sir} \\ $$
