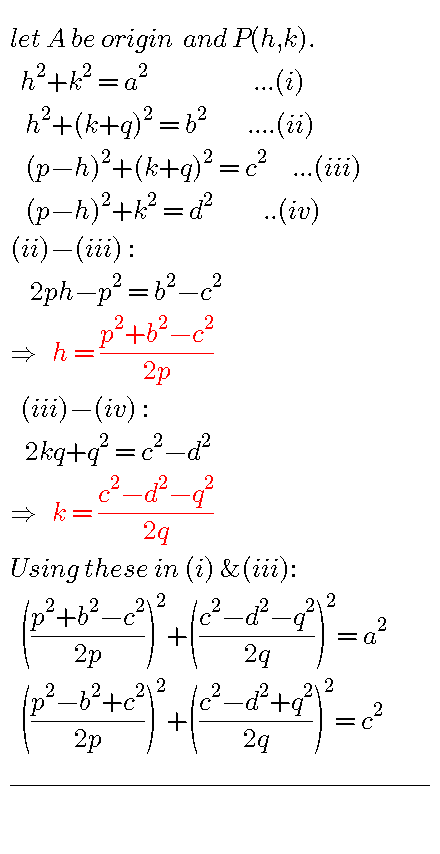Question Number 49651 by ajfour last updated on 08/Dec/18
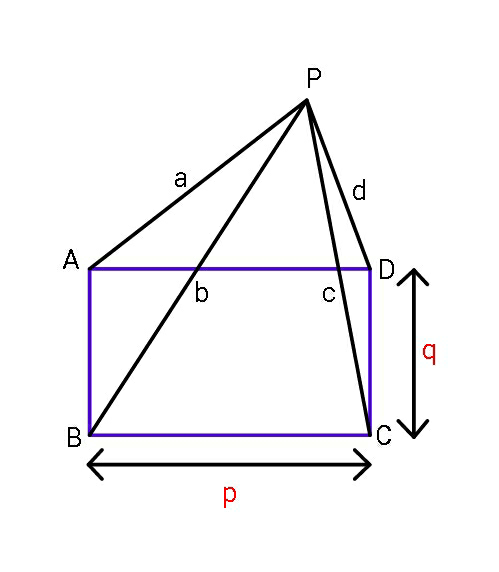
Commented by ajfour last updated on 08/Dec/18
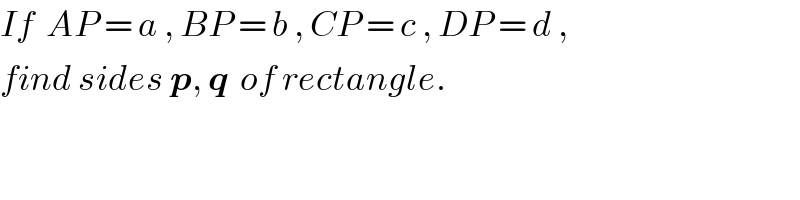
$${If}\:\:{AP}\:=\:{a}\:,\:{BP}\:=\:{b}\:,\:{CP}\:=\:{c}\:,\:{DP}\:=\:{d}\:, \\ $$$${find}\:{sides}\:\boldsymbol{{p}},\:\boldsymbol{{q}}\:\:{of}\:{rectangle}. \\ $$
Commented by mr W last updated on 09/Dec/18
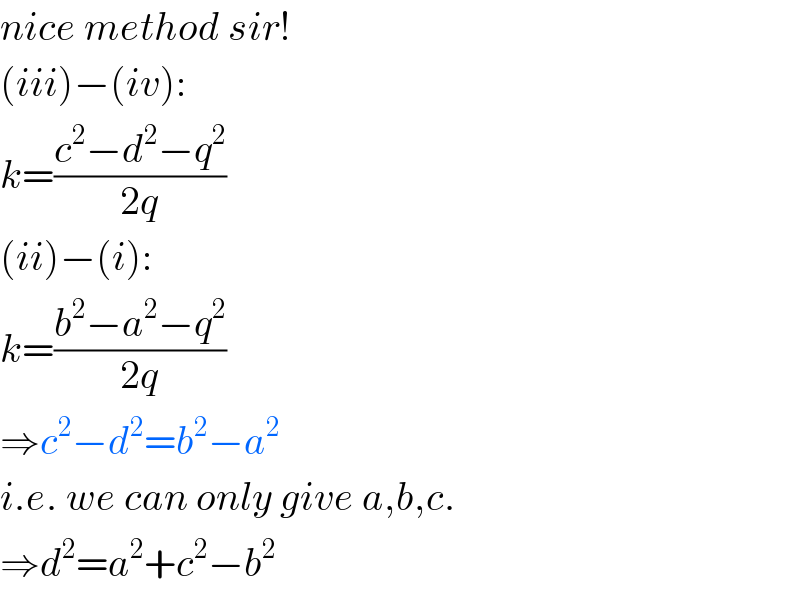
$${nice}\:{method}\:{sir}! \\ $$$$\left({iii}\right)−\left({iv}\right): \\ $$$${k}=\frac{{c}^{\mathrm{2}} −{d}^{\mathrm{2}} −{q}^{\mathrm{2}} }{\mathrm{2}{q}} \\ $$$$\left({ii}\right)−\left({i}\right): \\ $$$${k}=\frac{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} −{q}^{\mathrm{2}} }{\mathrm{2}{q}} \\ $$$$\Rightarrow{c}^{\mathrm{2}} −{d}^{\mathrm{2}} ={b}^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$${i}.{e}.\:{we}\:{can}\:{only}\:{give}\:{a},{b},{c}. \\ $$$$\Rightarrow{d}^{\mathrm{2}} ={a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$
Commented by ajfour last updated on 09/Dec/18