Question-49660

Question Number 49660 by Rio Michael last updated on 08/Dec/18

Commented by Rio Michael last updated on 08/Dec/18

Above is a Circle with centre O .If it has radius of 10cm find the lenght of the line AC.Note : ∠AOC=30°

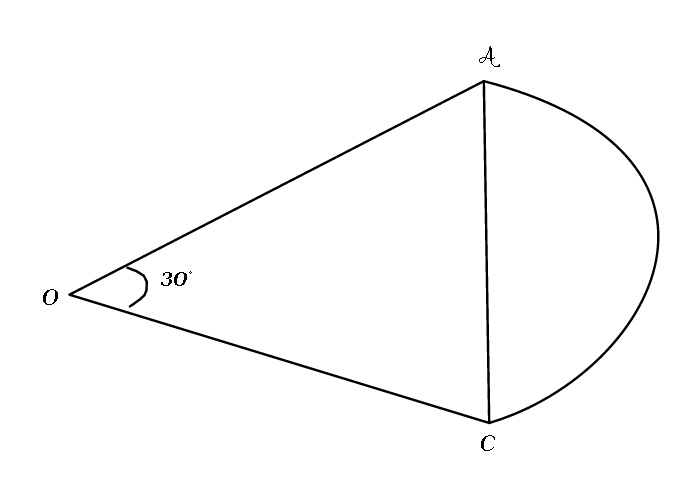
$${Above}\:{is}\:{a}\:{Circle}\:{with}\:{centre}\:{O}\:.{If}\:{it}\:{has}\:{radius}\:{of}\:\mathrm{10}{cm} \\ $$$${find}\:{the}\:{lenght}\:{of}\:{the}\:{line}\:{AC}.{Note}\::\:\angle{AOC}=\mathrm{30}° \\ $$

Answered by math1967 last updated on 09/Dec/18

((AC)/(sin30))=((AO)/(sin75)) [AO=OC ∠OAC=∠OCA=((180−30)/2)] ∴AC=((10×sin 30)/(sin75))=(5/(.96))=5.21cm (approx)

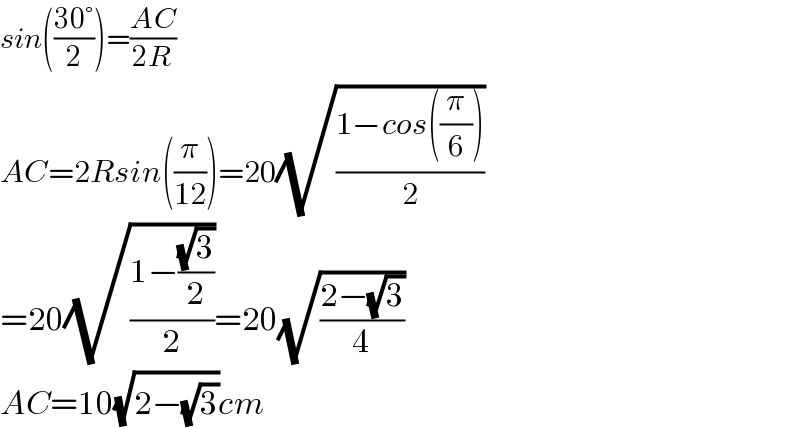
$$\frac{{AC}}{{sin}\mathrm{30}}=\frac{{AO}}{{sin}\mathrm{75}}\:\left[{AO}={OC}\:\angle{OAC}=\angle{OCA}=\frac{\mathrm{180}−\mathrm{30}}{\mathrm{2}}\right] \\ $$$$\therefore{AC}=\frac{\mathrm{10}×\mathrm{sin}\:\mathrm{30}}{{sin}\mathrm{75}}=\frac{\mathrm{5}}{.\mathrm{96}}=\mathrm{5}.\mathrm{21}{cm}\:\left({approx}\right) \\ $$

Answered by Smail last updated on 09/Dec/18

sin(((30°)/2))=((AC)/(2R)) AC=2Rsin((π/(12)))=20(√((1−cos((π/6)))/2)) =20(√((1−((√3)/2))/2))=20(√((2−(√3))/4)) AC=10(√(2−(√3)))cm

$${sin}\left(\frac{\mathrm{30}°}{\mathrm{2}}\right)=\frac{{AC}}{\mathrm{2}{R}} \\ $$$${AC}=\mathrm{2}{Rsin}\left(\frac{\pi}{\mathrm{12}}\right)=\mathrm{20}\sqrt{\frac{\mathrm{1}−{cos}\left(\frac{\pi}{\mathrm{6}}\right)}{\mathrm{2}}} \\ $$$$=\mathrm{20}\sqrt{\frac{\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\mathrm{2}}}=\mathrm{20}\sqrt{\frac{\mathrm{2}−\sqrt{\mathrm{3}}}{\mathrm{4}}} \\ $$$${AC}=\mathrm{10}\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}{cm} \\ $$

Commented by Rio Michael last updated on 09/Dec/18

$${wow}\:{thanks} \\ $$

Facebook Tweet Pin

Question-49660

Leave a Reply Cancel reply