Question Number 49678 by Rio Michael last updated on 09/Dec/18
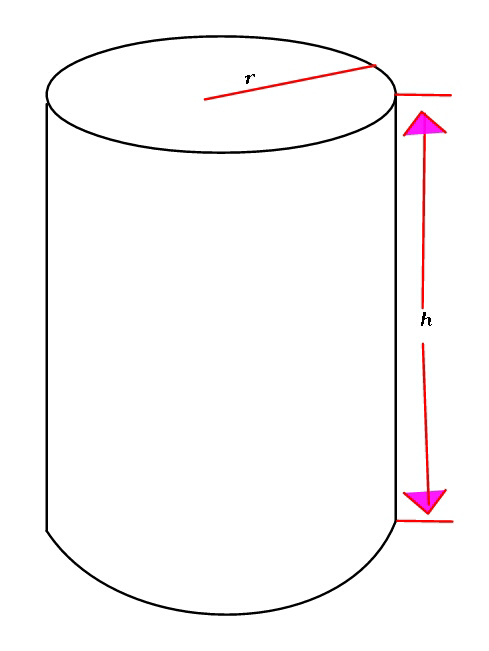
Commented by Rio Michael last updated on 09/Dec/18

$${A}\:{closed}\:{Cylinder}\:{can}\:{is}\:{made}\:{from}\:{a}\:{fix}\:{amount}\:{A}\:{of}\:{thin} \\ $$$${metal}\:{sheet}.{Find}\:{the}\:{relation}\:{between}\:{its}\:{radius}\:{and}\:{height}, \\ $$$${if}\:{it}\:{is}\:{to}\:{contain}\:{the}\:{maximum}\:{possible}\:{volume} \\ $$$$\left({Note}:\:{Wastage}\:{of}\:{material}\:{ignored}\right). \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 09/Dec/18
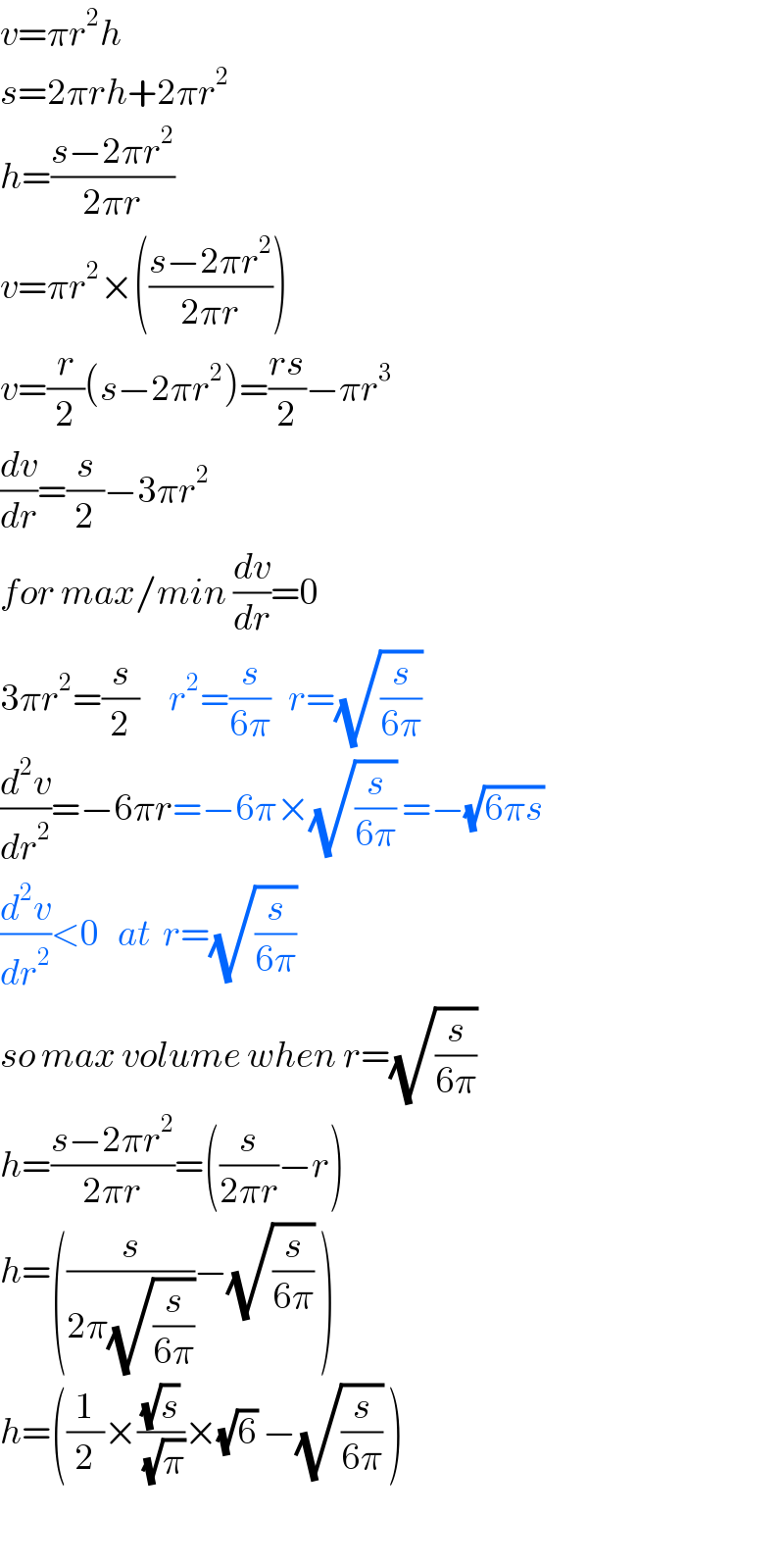
$${v}=\pi{r}^{\mathrm{2}} {h} \\ $$$${s}=\mathrm{2}\pi{rh}+\mathrm{2}\pi{r}^{\mathrm{2}} \:\: \\ $$$${h}=\frac{{s}−\mathrm{2}\pi{r}^{\mathrm{2}} }{\mathrm{2}\pi{r}} \\ $$$${v}=\pi{r}^{\mathrm{2}} ×\left(\frac{{s}−\mathrm{2}\pi{r}^{\mathrm{2}} }{\mathrm{2}\pi{r}}\right) \\ $$$${v}=\frac{{r}}{\mathrm{2}}\left({s}−\mathrm{2}\pi{r}^{\mathrm{2}} \right)=\frac{{rs}}{\mathrm{2}}−\pi{r}^{\mathrm{3}} \\ $$$$\frac{{dv}}{{dr}}=\frac{{s}}{\mathrm{2}}−\mathrm{3}\pi{r}^{\mathrm{2}} \\ $$$${for}\:{max}/{min}\:\frac{{dv}}{{dr}}=\mathrm{0} \\ $$$$\mathrm{3}\pi{r}^{\mathrm{2}} =\frac{{s}}{\mathrm{2}}\:\:\:\:\:{r}^{\mathrm{2}} =\frac{{s}}{\mathrm{6}\pi}\:\:\:{r}=\sqrt{\frac{{s}}{\mathrm{6}\pi}}\: \\ $$$$\frac{{d}^{\mathrm{2}} {v}}{{dr}^{\mathrm{2}} }=−\mathrm{6}\pi{r}=−\mathrm{6}\pi×\sqrt{\frac{{s}}{\mathrm{6}\pi}}\:=−\sqrt{\mathrm{6}\pi{s}}\: \\ $$$$\frac{{d}^{\mathrm{2}} {v}}{{dr}^{\mathrm{2}} }<\mathrm{0}\:\:\:{at}\:\:{r}=\sqrt{\frac{{s}}{\mathrm{6}\pi}}\: \\ $$$${so}\:{max}\:{volume}\:{when}\:{r}=\sqrt{\frac{{s}}{\mathrm{6}\pi}}\: \\ $$$${h}=\frac{{s}−\mathrm{2}\pi{r}^{\mathrm{2}} }{\mathrm{2}\pi{r}}=\left(\frac{{s}}{\mathrm{2}\pi{r}}−{r}\right)\: \\ $$$${h}=\left(\frac{{s}}{\mathrm{2}\pi\sqrt{\frac{{s}}{\mathrm{6}\pi}}}−\sqrt{\frac{{s}}{\mathrm{6}\pi}}\:\right) \\ $$$${h}=\left(\frac{\mathrm{1}}{\mathrm{2}}×\frac{\sqrt{{s}}}{\:\sqrt{\pi}}×\sqrt{\mathrm{6}}\:−\sqrt{\frac{{s}}{\mathrm{6}\pi}}\:\right) \\ $$$$ \\ $$
Commented by Rio Michael last updated on 09/Dec/18
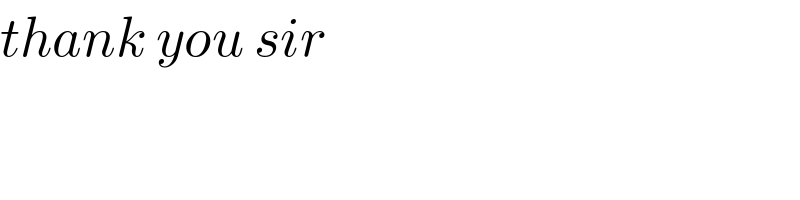
$${thank}\:{you}\:{sir} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Dec/18

$${most}\:{welcome}… \\ $$
