Question Number 49740 by ajfour last updated on 09/Dec/18
Commented by ajfour last updated on 09/Dec/18

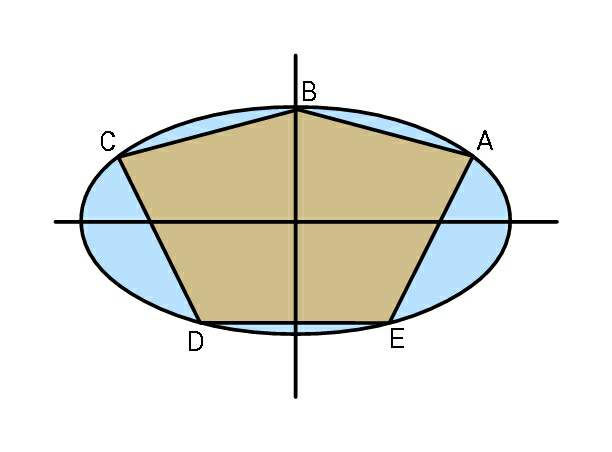
$${Find}\:{side}\:{length}\:\boldsymbol{{s}}\:{of}\:{a}\:{pentagon} \\ $$$${of}\:{equal}\:{sides}\:{inscribed}\:{within} \\ $$$${the}\:{ellipse},\:{in}\:{terms}\:{of}\:{ellipse} \\ $$$${parameters}\:\boldsymbol{{a}}\:{and}\:\boldsymbol{{b}}. \\ $$
Answered by ajfour last updated on 10/Dec/18
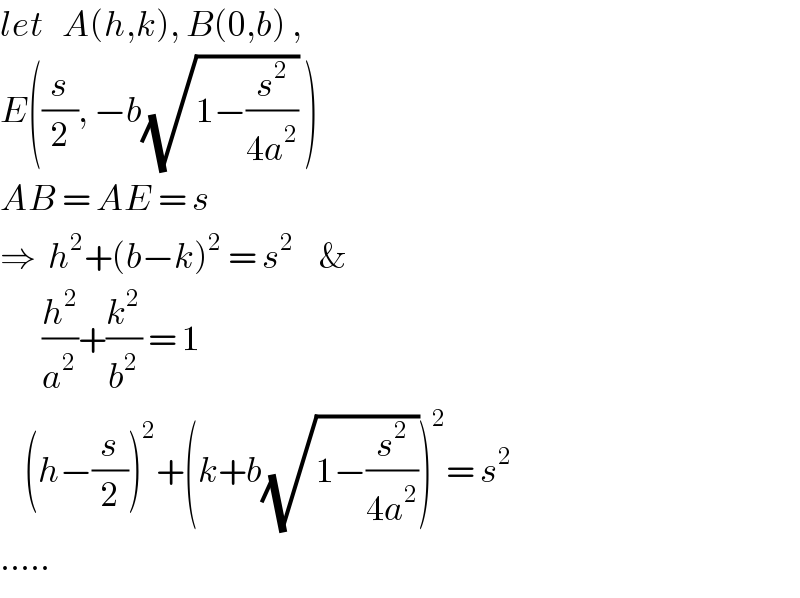
$${let}\:\:\:{A}\left({h},{k}\right),\:{B}\left(\mathrm{0},{b}\right)\:, \\ $$$${E}\left(\frac{{s}}{\mathrm{2}},\:−{b}\sqrt{\mathrm{1}−\frac{{s}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }}\:\right) \\ $$$${AB}\:=\:{AE}\:=\:{s} \\ $$$$\Rightarrow\:\:{h}^{\mathrm{2}} +\left({b}−{k}\right)^{\mathrm{2}} \:=\:{s}^{\mathrm{2}} \:\:\:\:\& \\ $$$$\:\:\:\:\:\:\:\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{k}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$$\:\:\:\:\left({h}−\frac{{s}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({k}+{b}\sqrt{\mathrm{1}−\frac{{s}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }}\right)^{\mathrm{2}} =\:{s}^{\mathrm{2}} \\ $$$$….. \\ $$
Commented by ajfour last updated on 10/Dec/18
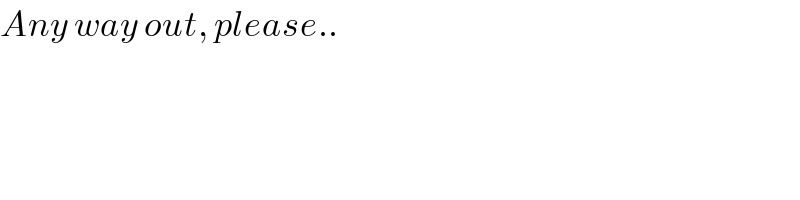
$${Any}\:{way}\:{out},\:{please}.. \\ $$
