Menu Close

Question-49859

Tinku Tara 0 Comments
Pin




Question Number 49859 by hassentimol last updated on 11/Dec/18
Commented by hassentimol last updated on 11/Dec/18
Could someone please explain me why this ? I know that 0.999...=1 is true but why the above shown is correct ? I don′t undersand it...
$$\mathrm{Could}\:\mathrm{someone}\:\mathrm{please}\:\mathrm{explain}\:\mathrm{me}\:\mathrm{why}\:\mathrm{this}\:? \\ $$$$\mathrm{I}\:\mathrm{know}\:\mathrm{that}\:\mathrm{0}.\mathrm{999}…=\mathrm{1}\:\mathrm{is}\:\mathrm{true}\:\mathrm{but}\:\mathrm{why}\:\mathrm{the} \\ $$$$\mathrm{above}\:\mathrm{shown}\:\mathrm{is}\:\mathrm{correct}\:?\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{undersand}\:\mathrm{it}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 11/Dec/18
Commented by tanmay.chaudhury50@gmail.com last updated on 11/Dec/18
Commented by maxmathsup by imad last updated on 11/Dec/18
we have 0,99..=0,9 +0,09 +..=(9/(10)) +(9/(100)) +(9/(1000)) +... =(9/(10))( 1 +(1/(10)) +(1/(100)) +...) =(9/(10))( 1+(1/(10)) +((1/(10)))^2 +...) =(9/(10)) .(1/(1−(1/(10)))) =1 ⇒ lim_(n→+∞) 0,999....9( with n 9)=1 ⇒[lim_(n→+∞) ]=1 but ∀n ∈N 0,999..(n 9) <1 ⇒[0,9999(n 9]=0 ⇒lim_(n→+∞) [....]=0
$${we}\:{have}\:\mathrm{0},\mathrm{99}..=\mathrm{0},\mathrm{9}\:+\mathrm{0},\mathrm{09}\:+..=\frac{\mathrm{9}}{\mathrm{10}}\:+\frac{\mathrm{9}}{\mathrm{100}}\:+\frac{\mathrm{9}}{\mathrm{1000}}\:+… \\ $$$$=\frac{\mathrm{9}}{\mathrm{10}}\left(\:\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{10}}\:+\frac{\mathrm{1}}{\mathrm{100}}\:+…\right)\:=\frac{\mathrm{9}}{\mathrm{10}}\left(\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{10}}\:+\left(\frac{\mathrm{1}}{\mathrm{10}}\right)^{\mathrm{2}} \:+…\right)\:=\frac{\mathrm{9}}{\mathrm{10}}\:.\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}}}\:=\mathrm{1}\:\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \mathrm{0},\mathrm{999}….\mathrm{9}\left(\:{with}\:{n}\:\mathrm{9}\right)=\mathrm{1}\:\Rightarrow\left[{lim}_{{n}\rightarrow+\infty} \right]=\mathrm{1} \\ $$$${but}\:\forall{n}\:\in{N}\:\:\:\mathrm{0},\mathrm{999}..\left({n}\:\mathrm{9}\right)\:<\mathrm{1}\:\Rightarrow\left[\mathrm{0},\mathrm{9999}\left({n}\:\mathrm{9}\right]=\mathrm{0}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \left[….\right]=\mathrm{0}\right. \\ $$
Answered by MJS last updated on 11/Dec/18
the ⌊ ⌋ make the difference ⌊x⌋ is the greatest integer ≤x ⌊lim_(n→∞) f(n)⌋ calculates the limit first. in our case the limit is 1, and ⌊1⌋=1 lim_(n→∞) ⌊f(n)⌋ calculates the limit of the greatest integer, ⌊0.9999...⌋=0, no matter how many 9s you add
$$\mathrm{the}\:\lfloor\:\rfloor\:\mathrm{make}\:\mathrm{the}\:\mathrm{difference} \\ $$$$\lfloor{x}\rfloor\:\mathrm{is}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{integer}\:\leqslant{x} \\ $$$$\lfloor\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{f}\left({n}\right)\rfloor\:\mathrm{calculates}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{first}.\:\mathrm{in}\:\mathrm{our} \\ $$$$\mathrm{case}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{is}\:\mathrm{1},\:\mathrm{and}\:\lfloor\mathrm{1}\rfloor=\mathrm{1} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\lfloor{f}\left({n}\right)\rfloor\:\mathrm{calculates}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{of}\:\mathrm{the}\:\mathrm{greatest} \\ $$$$\mathrm{integer},\:\lfloor\mathrm{0}.\mathrm{9999}…\rfloor=\mathrm{0},\:\mathrm{no}\:\mathrm{matter}\:\mathrm{how}\:\mathrm{many} \\ $$$$\mathrm{9s}\:\mathrm{you}\:\mathrm{add} \\ $$
Answered by mr W last updated on 11/Dec/18
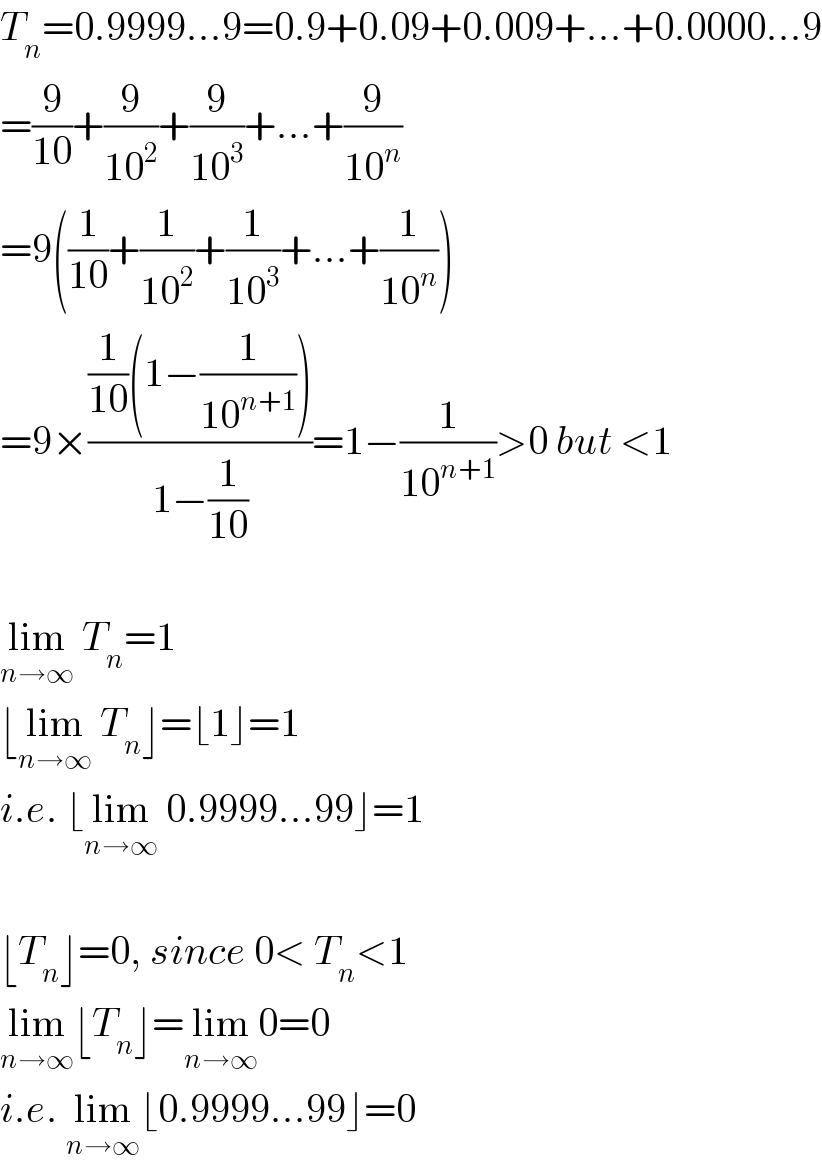
T_n =0.9999...9=0.9+0.09+0.009+...+0.0000...9 =(9/(10))+(9/(10^2 ))+(9/(10^3 ))+...+(9/(10^n )) =9((1/(10))+(1/(10^2 ))+(1/(10^3 ))+...+(1/(10^n ))) =9×(((1/(10))(1−(1/(10^(n+1) ))))/(1−(1/(10))))=1−(1/(10^(n+1) ))>0 but <1 lim_(n→∞) T_n =1 ⌊lim_(n→∞) T_n ⌋=⌊1⌋=1 i.e. ⌊lim_(n→∞) 0.9999...99⌋=1 ⌊T_n ⌋=0, since 0< T_n <1 lim_(n→∞) ⌊T_n ⌋=lim_(n→∞) 0=0 i.e. lim_(n→∞) ⌊0.9999...99⌋=0
$${T}_{{n}} =\mathrm{0}.\mathrm{9999}…\mathrm{9}=\mathrm{0}.\mathrm{9}+\mathrm{0}.\mathrm{09}+\mathrm{0}.\mathrm{009}+…+\mathrm{0}.\mathrm{0000}…\mathrm{9} \\ $$$$=\frac{\mathrm{9}}{\mathrm{10}}+\frac{\mathrm{9}}{\mathrm{10}^{\mathrm{2}} }+\frac{\mathrm{9}}{\mathrm{10}^{\mathrm{3}} }+…+\frac{\mathrm{9}}{\mathrm{10}^{{n}} } \\ $$$$=\mathrm{9}\left(\frac{\mathrm{1}}{\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{10}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{10}^{\mathrm{3}} }+…+\frac{\mathrm{1}}{\mathrm{10}^{{n}} }\right) \\ $$$$=\mathrm{9}×\frac{\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}^{{n}+\mathrm{1}} }\right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}^{{n}+\mathrm{1}} }>\mathrm{0}\:{but}\:<\mathrm{1} \\ $$$$ \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{T}_{{n}} =\mathrm{1} \\ $$$$\lfloor\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{T}_{{n}} \rfloor=\lfloor\mathrm{1}\rfloor=\mathrm{1} \\ $$$${i}.{e}.\:\lfloor\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{0}.\mathrm{9999}…\mathrm{99}\rfloor=\mathrm{1} \\ $$$$ \\ $$$$\lfloor{T}_{{n}} \rfloor=\mathrm{0},\:{since}\:\mathrm{0}<\:{T}_{{n}} <\mathrm{1} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\lfloor{T}_{{n}} \rfloor=\underset{{n}\rightarrow\infty} {\mathrm{lim}0}=\mathrm{0} \\ $$$${i}.{e}.\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\lfloor\mathrm{0}.\mathrm{9999}…\mathrm{99}\rfloor=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *