Menu Close

Question-49877

Tinku Tara 0 Comments
Pin




Question Number 49877 by ajfour last updated on 11/Dec/18
Commented by ajfour last updated on 11/Dec/18
Find maximum area in blue.
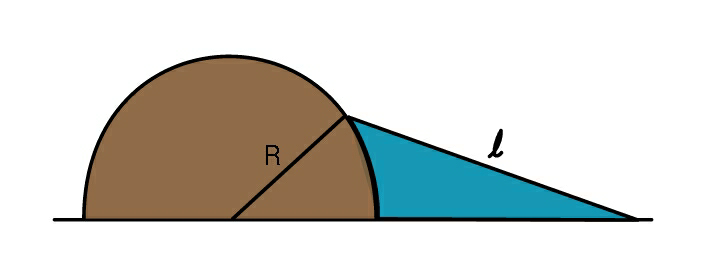
$${Find}\:{maximum}\:{area}\:{in}\:{blue}. \\ $$
Answered by mr W last updated on 12/Dec/18
((sin α)/R)=((sin θ)/l) ⇒sin α=(R/l) sin θ=((sin θ)/λ) cos α (dα/dθ)=(1/λ)cos θ A_(blue) =((Rl)/2) sin (α+θ)−((R^2 θ)/2) A=(R^2 /2)[(l/R) sin (α+θ)−θ] A=(R^2 /2)[λ sin (α+θ)−θ]=(R^2 /2)f(θ) f(θ)=λ sin (α+θ)−θ ((df(θ))/dθ)=λ cos (α+θ)((dα/dθ)+1)−1=λ cos (α+θ)((1/(λ cos α)) cos θ+1)−1=0 ⇒cos (α+θ)(((cos θ)/(cos α))+λ)−1=0 ⇒(cos α cos θ−sin α sin θ)(((cos θ)/(cos α))+λ)−1=0 ⇒(cos θ−tan α sin θ)(cos θ+λ cos α)−1=0 ⇒(cos θ−((sin^2 θ)/( (√(λ^2 −sin^2 θ)))))(1+((√(λ^2 −sin^2 θ))/λ^2 ))−1=0 ⇒θ=..... with λ=2/1=2,⇒θ=47.06°⇒A=0.5199
$$\frac{\mathrm{sin}\:\alpha}{{R}}=\frac{\mathrm{sin}\:\theta}{{l}} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{{R}}{{l}}\:\mathrm{sin}\:\theta=\frac{\mathrm{sin}\:\theta}{\lambda} \\ $$$$\mathrm{cos}\:\alpha\:\frac{{d}\alpha}{{d}\theta}=\frac{\mathrm{1}}{\lambda}\mathrm{cos}\:\theta \\ $$$${A}_{{blue}} =\frac{{Rl}}{\mathrm{2}}\:\mathrm{sin}\:\left(\alpha+\theta\right)−\frac{{R}^{\mathrm{2}} \theta}{\mathrm{2}} \\ $$$${A}=\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left[\frac{{l}}{{R}}\:\mathrm{sin}\:\left(\alpha+\theta\right)−\theta\right] \\ $$$${A}=\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left[\lambda\:\mathrm{sin}\:\left(\alpha+\theta\right)−\theta\right]=\frac{{R}^{\mathrm{2}} }{\mathrm{2}}{f}\left(\theta\right) \\ $$$${f}\left(\theta\right)=\lambda\:\mathrm{sin}\:\left(\alpha+\theta\right)−\theta \\ $$$$\frac{{df}\left(\theta\right)}{{d}\theta}=\lambda\:\mathrm{cos}\:\left(\alpha+\theta\right)\left(\frac{{d}\alpha}{{d}\theta}+\mathrm{1}\right)−\mathrm{1}=\lambda\:\mathrm{cos}\:\left(\alpha+\theta\right)\left(\frac{\mathrm{1}}{\lambda\:\mathrm{cos}\:\alpha}\:\mathrm{cos}\:\theta+\mathrm{1}\right)−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\left(\alpha+\theta\right)\left(\frac{\mathrm{cos}\:\theta}{\mathrm{cos}\:\alpha}+\lambda\right)−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{cos}\:\alpha\:\mathrm{cos}\:\theta−\mathrm{sin}\:\alpha\:\mathrm{sin}\:\theta\right)\left(\frac{\mathrm{cos}\:\theta}{\mathrm{cos}\:\alpha}+\lambda\right)−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{cos}\:\theta−\mathrm{tan}\:\alpha\:\mathrm{sin}\:\theta\right)\left(\mathrm{cos}\:\theta+\lambda\:\mathrm{cos}\:\alpha\right)−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{cos}\:\theta−\frac{\mathrm{sin}^{\mathrm{2}} \:\theta}{\:\sqrt{\lambda^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\theta}}\right)\left(\mathrm{1}+\frac{\sqrt{\lambda^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\theta}}{\lambda^{\mathrm{2}} }\right)−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\theta=….. \\ $$$${with}\:\lambda=\mathrm{2}/\mathrm{1}=\mathrm{2},\Rightarrow\theta=\mathrm{47}.\mathrm{06}°\Rightarrow{A}=\mathrm{0}.\mathrm{5199} \\ $$
Commented by ajfour last updated on 11/Dec/18
Thanks Sir!
$${Thanks}\:{Sir}! \\ $$
Answered by MJS last updated on 11/Dec/18
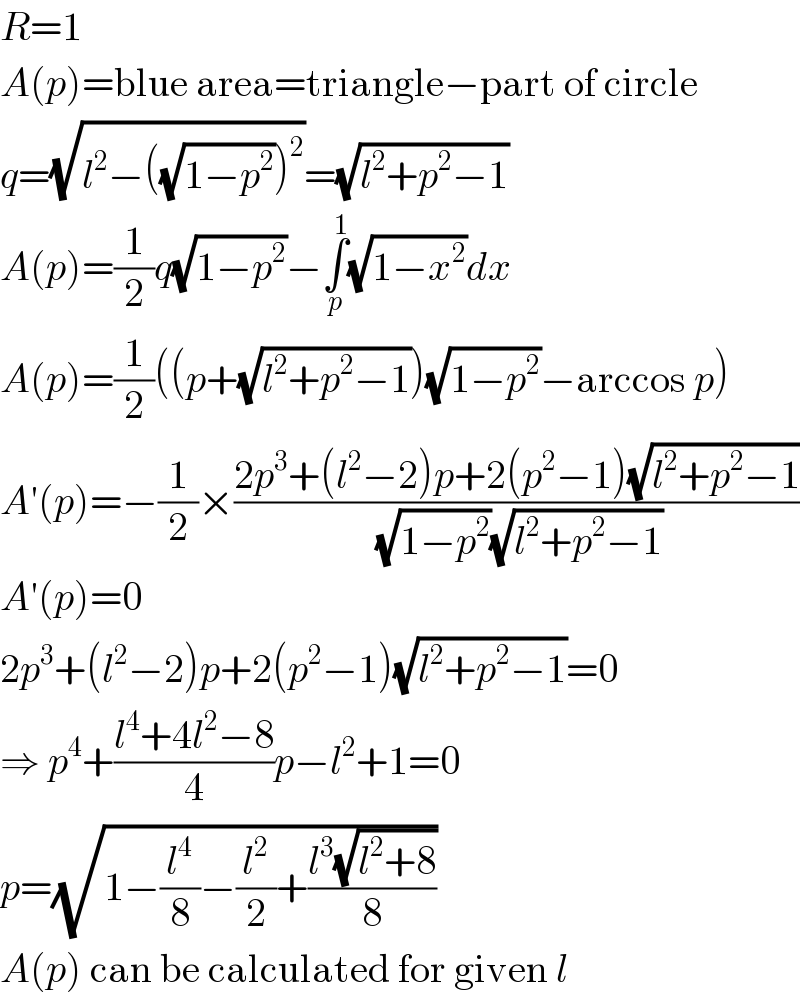
R=1 A(p)=blue area=triangle−part of circle q=(√(l^2 −((√(1−p^2 )))^2 ))=(√(l^2 +p^2 −1)) A(p)=(1/2)q(√(1−p^2 ))−∫_p ^1 (√(1−x^2 ))dx A(p)=(1/2)((p+(√(l^2 +p^2 −1)))(√(1−p^2 ))−arccos p) A′(p)=−(1/2)×((2p^3 +(l^2 −2)p+2(p^2 −1)(√(l^2 +p^2 −1)))/( (√(1−p^2 ))(√(l^2 +p^2 −1)))) A′(p)=0 2p^3 +(l^2 −2)p+2(p^2 −1)(√(l^2 +p^2 −1))=0 ⇒ p^4 +((l^4 +4l^2 −8)/4)p−l^2 +1=0 p=(√(1−(l^4 /8)−(l^2 /2)+((l^3 (√(l^2 +8)))/8))) A(p) can be calculated for given l
$${R}=\mathrm{1} \\ $$$${A}\left({p}\right)=\mathrm{blue}\:\mathrm{area}=\mathrm{triangle}−\mathrm{part}\:\mathrm{of}\:\mathrm{circle} \\ $$$${q}=\sqrt{{l}^{\mathrm{2}} −\left(\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }\right)^{\mathrm{2}} }=\sqrt{{l}^{\mathrm{2}} +{p}^{\mathrm{2}} −\mathrm{1}} \\ $$$${A}\left({p}\right)=\frac{\mathrm{1}}{\mathrm{2}}{q}\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }−\underset{{p}} {\overset{\mathrm{1}} {\int}}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$${A}\left({p}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\left({p}+\sqrt{{l}^{\mathrm{2}} +{p}^{\mathrm{2}} −\mathrm{1}}\right)\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }−\mathrm{arccos}\:{p}\right) \\ $$$${A}'\left({p}\right)=−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}{p}^{\mathrm{3}} +\left({l}^{\mathrm{2}} −\mathrm{2}\right){p}+\mathrm{2}\left({p}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{{l}^{\mathrm{2}} +{p}^{\mathrm{2}} −\mathrm{1}}}{\:\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }\sqrt{{l}^{\mathrm{2}} +{p}^{\mathrm{2}} −\mathrm{1}}} \\ $$$${A}'\left({p}\right)=\mathrm{0} \\ $$$$\mathrm{2}{p}^{\mathrm{3}} +\left({l}^{\mathrm{2}} −\mathrm{2}\right){p}+\mathrm{2}\left({p}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{{l}^{\mathrm{2}} +{p}^{\mathrm{2}} −\mathrm{1}}=\mathrm{0} \\ $$$$\Rightarrow\:{p}^{\mathrm{4}} +\frac{{l}^{\mathrm{4}} +\mathrm{4}{l}^{\mathrm{2}} −\mathrm{8}}{\mathrm{4}}{p}−{l}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${p}=\sqrt{\mathrm{1}−\frac{{l}^{\mathrm{4}} }{\mathrm{8}}−\frac{{l}^{\mathrm{2}} }{\mathrm{2}}+\frac{{l}^{\mathrm{3}} \sqrt{{l}^{\mathrm{2}} +\mathrm{8}}}{\mathrm{8}}} \\ $$$${A}\left({p}\right)\:\mathrm{can}\:\mathrm{be}\:\mathrm{calculated}\:\mathrm{for}\:\mathrm{given}\:{l} \\ $$
Commented by ajfour last updated on 11/Dec/18
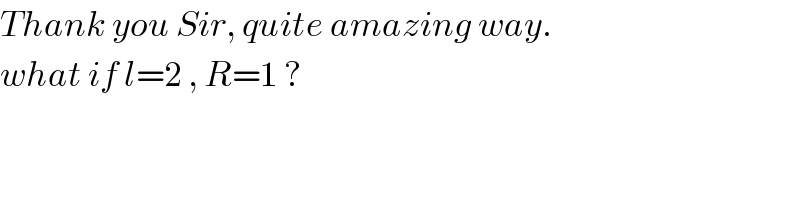
Thank you Sir, quite amazing way. what if l=2 , R=1 ?
$${Thank}\:{you}\:{Sir},\:{quite}\:{amazing}\:{way}. \\ $$$${what}\:{if}\:{l}=\mathrm{2}\:,\:{R}=\mathrm{1}\:? \\ $$
Commented by MJS last updated on 11/Dec/18
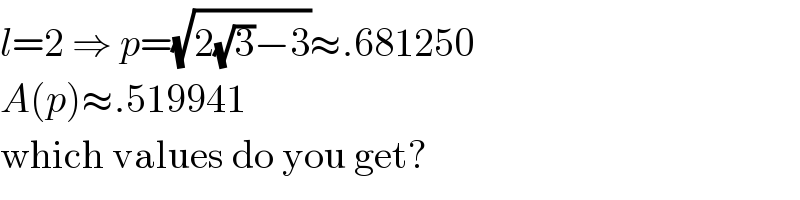
l=2 ⇒ p=(√(2(√3)−3))≈.681250 A(p)≈.519941 which values do you get?
$${l}=\mathrm{2}\:\Rightarrow\:{p}=\sqrt{\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}}\approx.\mathrm{681250} \\ $$$${A}\left({p}\right)\approx.\mathrm{519941} \\ $$$$\mathrm{which}\:\mathrm{values}\:\mathrm{do}\:\mathrm{you}\:\mathrm{get}? \\ $$
Commented by mr W last updated on 12/Dec/18
I got the same value A≈0.5199.
$${I}\:{got}\:{the}\:{same}\:{value}\:{A}\approx\mathrm{0}.\mathrm{5199}. \\ $$
Answered by ajfour last updated on 12/Dec/18
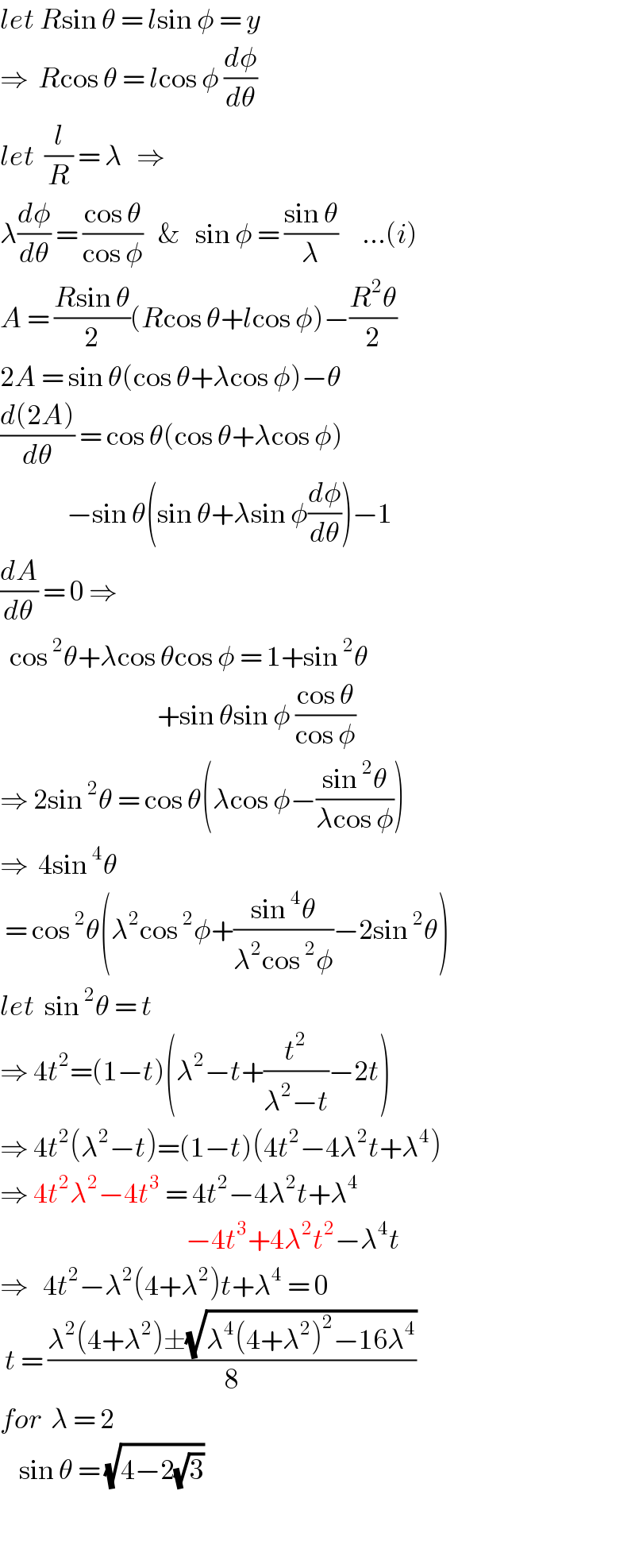
let Rsin θ = lsin φ = y ⇒ Rcos θ = lcos φ (dφ/dθ) let (l/R) = λ ⇒ λ(dφ/dθ) = ((cos θ)/(cos φ)) & sin φ = ((sin θ)/λ) ...(i) A = ((Rsin θ)/2)(Rcos θ+lcos φ)−((R^2 θ)/2) 2A = sin θ(cos θ+λcos φ)−θ ((d(2A))/dθ) = cos θ(cos θ+λcos φ) −sin θ(sin θ+λsin φ(dφ/dθ))−1 (dA/dθ) = 0 ⇒ cos^2 θ+λcos θcos φ = 1+sin^2 θ +sin θsin φ ((cos θ)/(cos φ)) ⇒ 2sin^2 θ = cos θ(λcos φ−((sin^2 θ)/(λcos φ))) ⇒ 4sin^4 θ = cos^2 θ(λ^2 cos^2 φ+((sin^4 θ)/(λ^2 cos^2 φ))−2sin^2 θ) let sin^2 θ = t ⇒ 4t^2 =(1−t)(λ^2 −t+(t^2 /(λ^2 −t))−2t) ⇒ 4t^2 (λ^2 −t)=(1−t)(4t^2 −4λ^2 t+λ^4 ) ⇒ 4t^2 λ^2 −4t^3 = 4t^2 −4λ^2 t+λ^4 −4t^3 +4λ^2 t^2 −λ^4 t ⇒ 4t^2 −λ^2 (4+λ^2 )t+λ^4 = 0 t = ((λ^2 (4+λ^2 )±(√(λ^4 (4+λ^2 )^2 −16λ^4 )))/8) for λ = 2 sin θ = (√(4−2(√3)))
$${let}\:{R}\mathrm{sin}\:\theta\:=\:{l}\mathrm{sin}\:\phi\:=\:{y} \\ $$$$\Rightarrow\:\:{R}\mathrm{cos}\:\theta\:=\:{l}\mathrm{cos}\:\phi\:\frac{{d}\phi}{{d}\theta} \\ $$$${let}\:\:\frac{{l}}{{R}}\:=\:\lambda\:\:\:\Rightarrow\:\: \\ $$$$\lambda\frac{{d}\phi}{{d}\theta}\:=\:\frac{\mathrm{cos}\:\theta}{\mathrm{cos}\:\phi}\:\:\:\&\:\:\:\mathrm{sin}\:\phi\:=\:\frac{\mathrm{sin}\:\theta}{\lambda}\:\:\:\:\:…\left({i}\right) \\ $$$${A}\:=\:\frac{{R}\mathrm{sin}\:\theta}{\mathrm{2}}\left({R}\mathrm{cos}\:\theta+{l}\mathrm{cos}\:\phi\right)−\frac{{R}^{\mathrm{2}} \theta}{\mathrm{2}} \\ $$$$\mathrm{2}{A}\:=\:\mathrm{sin}\:\theta\left(\mathrm{cos}\:\theta+\lambda\mathrm{cos}\:\phi\right)−\theta \\ $$$$\frac{{d}\left(\mathrm{2}{A}\right)}{{d}\theta}\:=\:\mathrm{cos}\:\theta\left(\mathrm{cos}\:\theta+\lambda\mathrm{cos}\:\phi\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{sin}\:\theta\left(\mathrm{sin}\:\theta+\lambda\mathrm{sin}\:\phi\frac{{d}\phi}{{d}\theta}\right)−\mathrm{1} \\ $$$$\frac{{dA}}{{d}\theta}\:=\:\mathrm{0}\:\Rightarrow \\ $$$$\:\:\mathrm{cos}\:^{\mathrm{2}} \theta+\lambda\mathrm{cos}\:\theta\mathrm{cos}\:\phi\:=\:\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{sin}\:\theta\mathrm{sin}\:\phi\:\frac{\mathrm{cos}\:\theta}{\mathrm{cos}\:\phi} \\ $$$$\Rightarrow\:\mathrm{2sin}\:^{\mathrm{2}} \theta\:=\:\mathrm{cos}\:\theta\left(\lambda\mathrm{cos}\:\phi−\frac{\mathrm{sin}\:^{\mathrm{2}} \theta}{\lambda\mathrm{cos}\:\phi}\right) \\ $$$$\Rightarrow\:\:\mathrm{4sin}\:^{\mathrm{4}} \theta\: \\ $$$$\:=\:\mathrm{cos}\:^{\mathrm{2}} \theta\left(\lambda^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi+\frac{\mathrm{sin}\:^{\mathrm{4}} \theta}{\lambda^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi}−\mathrm{2sin}\:^{\mathrm{2}} \theta\right) \\ $$$${let}\:\:\mathrm{sin}\:^{\mathrm{2}} \theta\:=\:{t} \\ $$$$\Rightarrow\:\mathrm{4}{t}^{\mathrm{2}} =\left(\mathrm{1}−{t}\right)\left(\lambda^{\mathrm{2}} −{t}+\frac{{t}^{\mathrm{2}} }{\lambda^{\mathrm{2}} −{t}}−\mathrm{2}{t}\right) \\ $$$$\Rightarrow\:\mathrm{4}{t}^{\mathrm{2}} \left(\lambda^{\mathrm{2}} −{t}\right)=\left(\mathrm{1}−{t}\right)\left(\mathrm{4}{t}^{\mathrm{2}} −\mathrm{4}\lambda^{\mathrm{2}} {t}+\lambda^{\mathrm{4}} \right) \\ $$$$\Rightarrow\:\mathrm{4}{t}^{\mathrm{2}} \lambda^{\mathrm{2}} −\mathrm{4}{t}^{\mathrm{3}} \:=\:\mathrm{4}{t}^{\mathrm{2}} −\mathrm{4}\lambda^{\mathrm{2}} {t}+\lambda^{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{4}{t}^{\mathrm{3}} +\mathrm{4}\lambda^{\mathrm{2}} {t}^{\mathrm{2}} −\lambda^{\mathrm{4}} {t} \\ $$$$\Rightarrow\:\:\:\mathrm{4}{t}^{\mathrm{2}} −\lambda^{\mathrm{2}} \left(\mathrm{4}+\lambda^{\mathrm{2}} \right){t}+\lambda^{\mathrm{4}} \:=\:\mathrm{0} \\ $$$$\:{t}\:=\:\frac{\lambda^{\mathrm{2}} \left(\mathrm{4}+\lambda^{\mathrm{2}} \right)\pm\sqrt{\lambda^{\mathrm{4}} \left(\mathrm{4}+\lambda^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{16}\lambda^{\mathrm{4}} }}{\mathrm{8}} \\ $$$${for}\:\:\lambda\:=\:\mathrm{2} \\ $$$$\:\:\:\:\mathrm{sin}\:\theta\:=\:\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}}\: \\ $$$$ \\ $$
Commented by ajfour last updated on 12/Dec/18
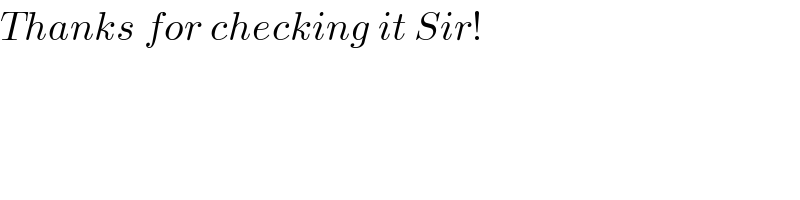
Thanks for checking it Sir!
$${Thanks}\:{for}\:{checking}\:{it}\:{Sir}! \\ $$
Commented by mr W last updated on 12/Dec/18
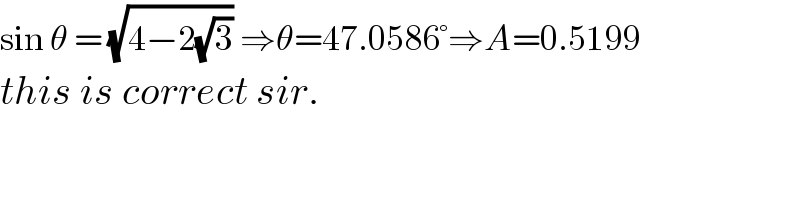
sin θ = (√(4−2(√3))) ⇒θ=47.0586°⇒A=0.5199 this is correct sir.
$$\mathrm{sin}\:\theta\:=\:\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}}\:\Rightarrow\theta=\mathrm{47}.\mathrm{0586}°\Rightarrow{A}=\mathrm{0}.\mathrm{5199} \\ $$$${this}\:{is}\:{correct}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *