Question Number 49903 by rahul 19 last updated on 12/Dec/18

Commented by rahul 19 last updated on 12/Dec/18
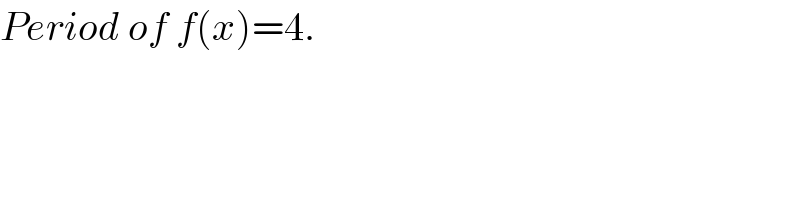
$${Period}\:{of}\:{f}\left({x}\right)=\mathrm{4}. \\ $$
Answered by mr W last updated on 12/Dec/18
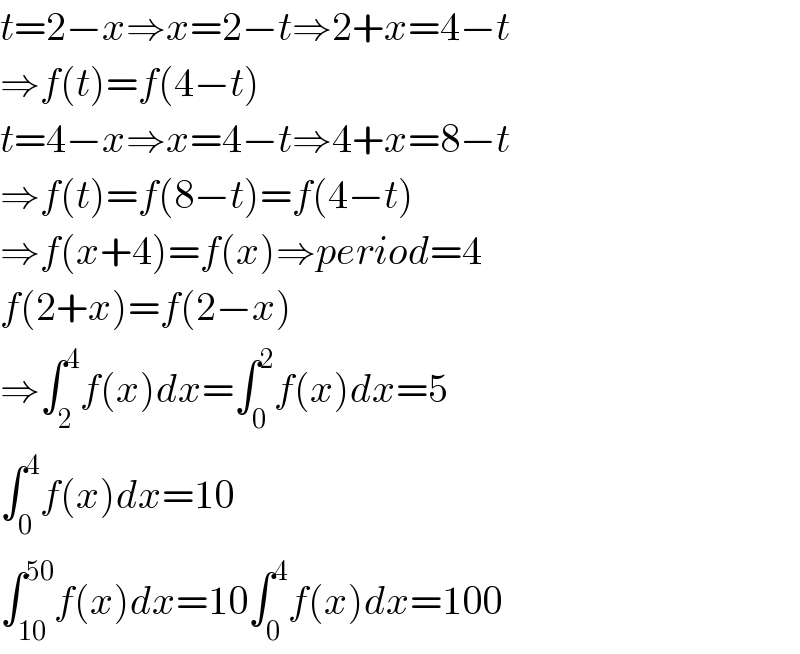
$${t}=\mathrm{2}−{x}\Rightarrow{x}=\mathrm{2}−{t}\Rightarrow\mathrm{2}+{x}=\mathrm{4}−{t} \\ $$$$\Rightarrow{f}\left({t}\right)={f}\left(\mathrm{4}−{t}\right) \\ $$$${t}=\mathrm{4}−{x}\Rightarrow{x}=\mathrm{4}−{t}\Rightarrow\mathrm{4}+{x}=\mathrm{8}−{t} \\ $$$$\Rightarrow{f}\left({t}\right)={f}\left(\mathrm{8}−{t}\right)={f}\left(\mathrm{4}−{t}\right) \\ $$$$\Rightarrow{f}\left({x}+\mathrm{4}\right)={f}\left({x}\right)\Rightarrow{period}=\mathrm{4} \\ $$$${f}\left(\mathrm{2}+{x}\right)={f}\left(\mathrm{2}−{x}\right) \\ $$$$\Rightarrow\int_{\mathrm{2}} ^{\mathrm{4}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\mathrm{2}} {f}\left({x}\right){dx}=\mathrm{5} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{4}} {f}\left({x}\right){dx}=\mathrm{10} \\ $$$$\int_{\mathrm{10}} ^{\mathrm{50}} {f}\left({x}\right){dx}=\mathrm{10}\int_{\mathrm{0}} ^{\mathrm{4}} {f}\left({x}\right){dx}=\mathrm{100} \\ $$
Commented by mr W last updated on 12/Dec/18
You are welcome!
Commented by rahul 19 last updated on 12/Dec/18
Danke Mien Herr! ��
Commented by mr W last updated on 12/Dec/18
Do you learn German in the school?
