Question Number 49922 by Pk1167156@gmail.com last updated on 12/Dec/18
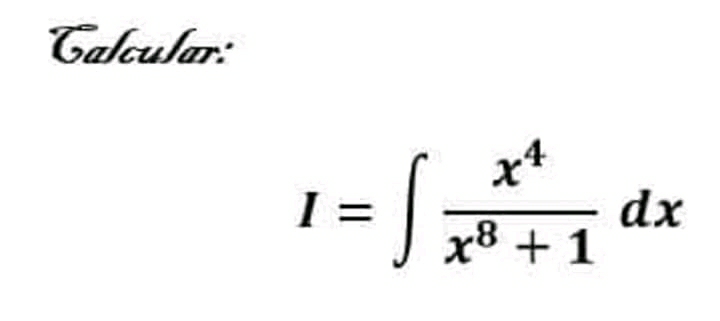
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Dec/18
![∫((x^4 dx)/(x^4 (x^4 +(1/x^4 )))) ∫(dx/(x^4 +(1/x^4 ))) ∫(dx/((x^2 +(1/x^2 ))^2 −2)) (1/2)∫(((1−(1/x^2 )+1+(1/x^2 )))/((x^2 +(1/x^2 ))^2 −2)) =(1/2)[∫((d(x+(1/x)))/({(x+(1/x))^2 −2}^2 −2))+∫((d(x−(1/x)))/({(x−(1/x))^2 +2}^2 −2))] =(1/2)[∫(dp/((p^2 −2)^2 −2))+∫(dq/((q^2 +2)^2 −2))] =(1/2)[∫(dp/(p^4 −4p^2 +2))+∫(dq/(q^4 +4q^2 +2))] =(1/2)[∫((1/p^2 )/(p^2 +(2/p^2 )−4))dp+∫((1/q^2 )/(q^2 +(2/q^2 )+4))]=(1/2)(I_1 +I_2 ) now solving I_1 ∫(([(1+((√2)/p^2 ))−(1−((√2)/p^2 ))]×(1/(2(√2))))/((p^2 +(2/p^2 ))−4))dp =(1/(2(√2)))∫((d(p−((√2)/p)))/((p−((√2)/p))^2 +2(√2) −4))−(1/(2(√2)))∫((d(p+((√2)/p)))/((p+((√2)/p))^2 −2(√2) −4)) =(1/(2(√2)))∫((d(p−((√2)/p)))/((p−((√2)/p))^2 −((√(4−2(√2))) )^2 )) −(1/(2(√2)))∫((d(p+((√2)/p)))/((p+((√2)/p))^2 −((√(4+2(√2))) )^2 )) =(1/(2(√2) ))×(1/(2((√(4−2(√2))))))×ln{(((p−((√2)/p))−(√(4−2(√2))))/((p−((√2)/p))+(√(4−2(√2)))))}−(1/(2(√2)))×(1/(2(√(4+2(√2))) ))ln{(((p+((√2)/p))−(√(4+2(√2))))/((p+((√2)/p))+(√(4+2(√2)))))}+c_1 p=(x+(1/x)) pls put p=x+(1/x) nxt going to find I_2 I=(1/2)(I_1 +I_2 ) ←required answer... now findngI_2 ∫((1/q^2 )/((q^2 +(2/q^2 ))+4))dq =(1/(2(√2)))∫(((1+((√2)/q^2 ))−(1−((√2)/q^2 )))/((q^2 +(2/q^2 ))+4))dq =(1/(2(√2)))∫((d(q−((√2)/q)))/((q−((√2)/q))^2 +2(√2) +4))−(1/(2(√2)))∫((d(q+((√2)/q)))/((q+((√2)/q))^2 +4−2(√2))) =(1/(2(√2)))×(1/( (√(4+2(√2)))))tan^(−1) (((q−((√2)/q))/( (√(4+2(√2))))))−(1/(2(√2)))×(1/( (√(4−2(√2)))))tan^(−1) (((q+((√2)/q))/( (√(4−2(√2))))))+c_2 pls put q=(x−(1/x)) so I=(1/2)(I_1 +I_2 )](https://www.tinkutara.com/question/Q49923.png)
$$\int\frac{{x}^{\mathrm{4}} {dx}}{{x}^{\mathrm{4}} \left({x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\right)} \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }} \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\int\frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}\right\}^{\mathrm{2}} −\mathrm{2}}+\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left\{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\right\}^{\mathrm{2}} −\mathrm{2}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\int\frac{{dp}}{\left({p}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}}+\int\frac{{dq}}{\left({q}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\int\frac{{dp}}{{p}^{\mathrm{4}} −\mathrm{4}{p}^{\mathrm{2}} +\mathrm{2}}+\int\frac{{dq}}{{q}^{\mathrm{4}} +\mathrm{4}{q}^{\mathrm{2}} +\mathrm{2}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\int\frac{\frac{\mathrm{1}}{{p}^{\mathrm{2}} }}{{p}^{\mathrm{2}} +\frac{\mathrm{2}}{{p}^{\mathrm{2}} }−\mathrm{4}}{dp}+\int\frac{\frac{\mathrm{1}}{{q}^{\mathrm{2}} }}{{q}^{\mathrm{2}} +\frac{\mathrm{2}}{{q}^{\mathrm{2}} }+\mathrm{4}}\right]=\frac{\mathrm{1}}{\mathrm{2}}\left({I}_{\mathrm{1}} +{I}_{\mathrm{2}} \right) \\ $$$${now}\:{solving}\:{I}_{\mathrm{1}} \\ $$$$\int\frac{\left[\left(\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{{p}^{\mathrm{2}} }\right)−\left(\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{{p}^{\mathrm{2}} }\right)\right]×\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}}{\left({p}^{\mathrm{2}} +\frac{\mathrm{2}}{{p}^{\mathrm{2}} }\right)−\mathrm{4}}{dp} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\frac{{d}\left({p}−\frac{\sqrt{\mathrm{2}}}{{p}}\right)}{\left({p}−\frac{\sqrt{\mathrm{2}}}{{p}}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}}\:−\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\frac{{d}\left({p}+\frac{\sqrt{\mathrm{2}}}{{p}}\right)}{\left({p}+\frac{\sqrt{\mathrm{2}}}{{p}}\right)^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}\:−\mathrm{4}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\frac{{d}\left({p}−\frac{\sqrt{\mathrm{2}}}{{p}}\right)}{\left({p}−\frac{\sqrt{\mathrm{2}}}{{p}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}\:\:\right)^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\frac{{d}\left({p}+\frac{\sqrt{\mathrm{2}}}{{p}}\right)}{\left({p}+\frac{\sqrt{\mathrm{2}}}{{p}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}}\:\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}\:}×\frac{\mathrm{1}}{\mathrm{2}\left(\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}\right)}×{ln}\left\{\frac{\left({p}−\frac{\sqrt{\mathrm{2}}}{{p}}\right)−\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}}{\left({p}−\frac{\sqrt{\mathrm{2}}}{{p}}\right)+\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}}\right\}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}×\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}}\:}{ln}\left\{\frac{\left({p}+\frac{\sqrt{\mathrm{2}}}{{p}}\right)−\sqrt{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}}}{\left({p}+\frac{\sqrt{\mathrm{2}}}{{p}}\right)+\sqrt{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}}}\right\}+{c}_{\mathrm{1}} \\ $$$${p}=\left({x}+\frac{\mathrm{1}}{{x}}\right) \\ $$$${pls}\:{put}\:{p}={x}+\frac{\mathrm{1}}{{x}} \\ $$$${nxt}\:{going}\:{to}\:{find}\:{I}_{\mathrm{2}} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\left({I}_{\mathrm{1}} +{I}_{\mathrm{2}} \right)\:\leftarrow{required}\:{answer}… \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{findngI}}_{\mathrm{2}} \\ $$$$\int\frac{\frac{\mathrm{1}}{{q}^{\mathrm{2}} }}{\left({q}^{\mathrm{2}} +\frac{\mathrm{2}}{{q}^{\mathrm{2}} }\right)+\mathrm{4}}{dq} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\frac{\left(\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{{q}^{\mathrm{2}} }\right)−\left(\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{{q}^{\mathrm{2}} }\right)}{\left({q}^{\mathrm{2}} +\frac{\mathrm{2}}{{q}^{\mathrm{2}} }\right)+\mathrm{4}}{dq} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\frac{{d}\left({q}−\frac{\sqrt{\mathrm{2}}}{{q}}\right)}{\left({q}−\frac{\sqrt{\mathrm{2}}}{{q}}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\frac{{d}\left({q}+\frac{\sqrt{\mathrm{2}}}{{q}}\right)}{\left({q}+\frac{\sqrt{\mathrm{2}}}{{q}}\right)^{\mathrm{2}} +\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}}}{tan}^{−\mathrm{1}} \left(\frac{{q}−\frac{\sqrt{\mathrm{2}}}{{q}}}{\:\sqrt{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}}}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}}{tan}^{−\mathrm{1}} \left(\frac{{q}+\frac{\sqrt{\mathrm{2}}}{{q}}}{\:\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}}\right)+{c}_{\mathrm{2}} \\ $$$${pls}\:{put}\:{q}=\left({x}−\frac{\mathrm{1}}{{x}}\right) \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{I}}=\frac{\mathrm{1}}{\mathrm{2}}\left({I}_{\mathrm{1}} +{I}_{\mathrm{2}} \right) \\ $$
Commented by Pk1167156@gmail.com last updated on 12/Dec/18
thank you very much sir.
Commented by tanmay.chaudhury50@gmail.com last updated on 12/Dec/18

$${most}\:{welcome}… \\ $$
