Menu Close

Question-49935

Tinku Tara 0 Comments
Pin




Question Number 49935 by ajfour last updated on 12/Dec/18
Commented by ajfour last updated on 12/Dec/18
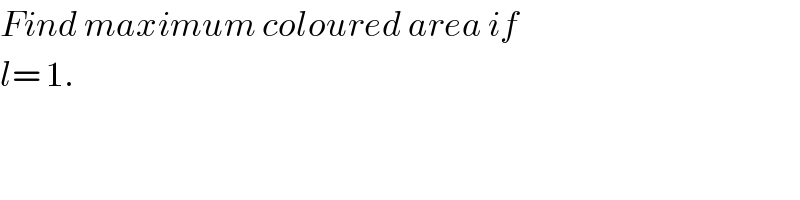
Find maximum coloured area if l= 1.
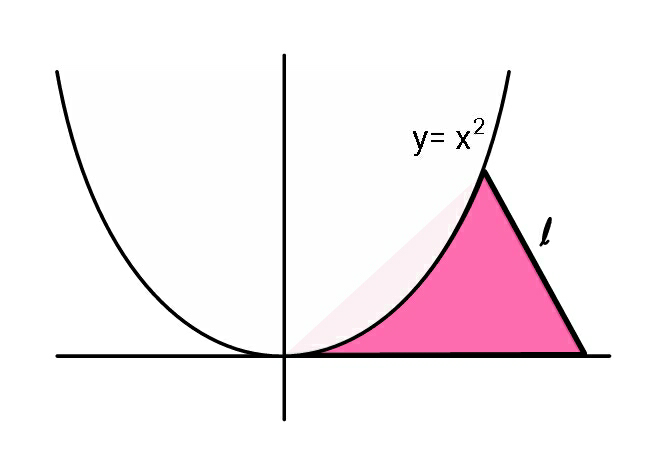
$${Find}\:{maximum}\:{coloured}\:{area}\:{if} \\ $$$${l}=\:\mathrm{1}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Dec/18
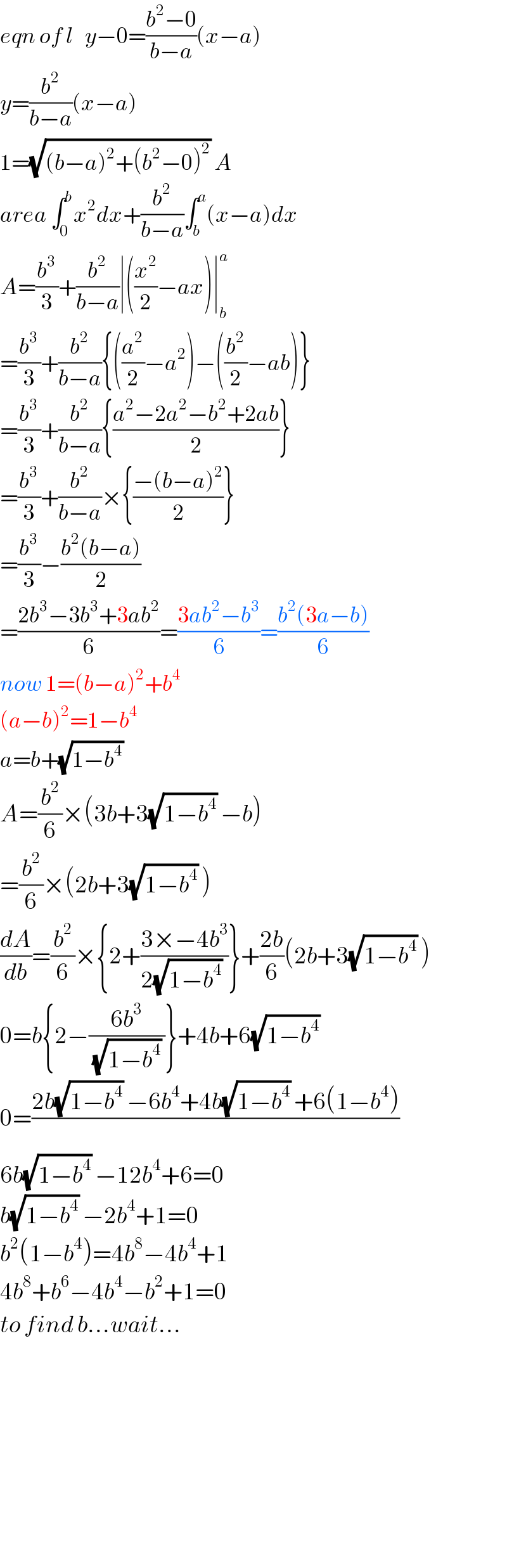
eqn of l y−0=((b^2 −0)/(b−a))(x−a) y=(b^2 /(b−a))(x−a) 1=(√((b−a)^2 +(b^2 −0)^2 )) A area ∫_0 ^b x^2 dx+(b^2 /(b−a))∫_b ^a (x−a)dx A=(b^3 /3)+(b^2 /(b−a))∣((x^2 /2)−ax)∣_b ^a =(b^3 /3)+(b^2 /(b−a)){((a^2 /2)−a^2 )−((b^2 /2)−ab)} =(b^3 /3)+(b^2 /(b−a)){((a^2 −2a^2 −b^2 +2ab)/2)} =(b^3 /3)+(b^2 /(b−a))×{((−(b−a)^2 )/2)} =(b^3 /3)−((b^2 (b−a))/2) =((2b^3 −3b^3 +3ab^2 )/6)=((3ab^2 −b^3 )/6)=((b^2 (3a−b))/6) now 1=(b−a)^2 +b^4 (a−b)^2 =1−b^4 a=b+(√(1−b^4 )) A=(b^2 /6)×(3b+3(√(1−b^4 )) −b) =(b^2 /6)×(2b+3(√(1−b^4 )) ) (dA/db)=(b^2 /6)×{2+((3×−4b^3 )/(2(√(1−b^4 )) ))}+((2b)/6)(2b+3(√(1−b^4 )) ) 0=b{2−((6b^3 )/( (√(1−b^4 )) ))}+4b+6(√(1−b^4 )) 0=((2b(√(1−b^4 )) −6b^4 +4b(√(1−b^4 )) +6(1−b^4 ))/) 6b(√(1−b^4 )) −12b^4 +6=0 b(√(1−b^4 )) −2b^4 +1=0 b^2 (1−b^4 )=4b^8 −4b^4 +1 4b^8 +b^6 −4b^4 −b^2 +1=0 to find b...wait...
$${eqn}\:{of}\:{l}\:\:\:{y}−\mathrm{0}=\frac{{b}^{\mathrm{2}} −\mathrm{0}}{{b}−{a}}\left({x}−{a}\right) \\ $$$${y}=\frac{{b}^{\mathrm{2}} }{{b}−{a}}\left({x}−{a}\right) \\ $$$$\mathrm{1}=\sqrt{\left({b}−{a}\right)^{\mathrm{2}} +\left({b}^{\mathrm{2}} −\mathrm{0}\right)^{\mathrm{2}} }\:{A} \\ $$$${area}\:\int_{\mathrm{0}} ^{{b}} {x}^{\mathrm{2}} {dx}+\frac{{b}^{\mathrm{2}} }{{b}−{a}}\int_{{b}} ^{{a}} \left({x}−{a}\right){dx} \\ $$$${A}=\frac{{b}^{\mathrm{3}} }{\mathrm{3}}+\frac{{b}^{\mathrm{2}} }{{b}−{a}}\mid\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−{ax}\right)\mid_{{b}} ^{{a}} \\ $$$$=\frac{{b}^{\mathrm{3}} }{\mathrm{3}}+\frac{{b}^{\mathrm{2}} }{{b}−{a}}\left\{\left(\frac{{a}^{\mathrm{2}} }{\mathrm{2}}−{a}^{\mathrm{2}} \right)−\left(\frac{{b}^{\mathrm{2}} }{\mathrm{2}}−{ab}\right)\right\} \\ $$$$=\frac{{b}^{\mathrm{3}} }{\mathrm{3}}+\frac{{b}^{\mathrm{2}} }{{b}−{a}}\left\{\frac{{a}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{2}{ab}}{\mathrm{2}}\right\} \\ $$$$=\frac{{b}^{\mathrm{3}} }{\mathrm{3}}+\frac{{b}^{\mathrm{2}} }{{b}−{a}}×\left\{\frac{−\left({b}−{a}\right)^{\mathrm{2}} }{\mathrm{2}}\right\} \\ $$$$=\frac{{b}^{\mathrm{3}} }{\mathrm{3}}−\frac{{b}^{\mathrm{2}} \left({b}−{a}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{2}{b}^{\mathrm{3}} −\mathrm{3}{b}^{\mathrm{3}} +\mathrm{3}{ab}^{\mathrm{2}} }{\mathrm{6}}=\frac{\mathrm{3}{ab}^{\mathrm{2}} −{b}^{\mathrm{3}} }{\mathrm{6}}=\frac{{b}^{\mathrm{2}} \left(\mathrm{3}{a}−{b}\right)}{\mathrm{6}} \\ $$$${now}\:\mathrm{1}=\left({b}−{a}\right)^{\mathrm{2}} +{b}^{\mathrm{4}} \\ $$$$\left({a}−{b}\right)^{\mathrm{2}} =\mathrm{1}−{b}^{\mathrm{4}} \\ $$$${a}={b}+\sqrt{\mathrm{1}−{b}^{\mathrm{4}} }\: \\ $$$${A}=\frac{{b}^{\mathrm{2}} }{\mathrm{6}}×\left(\mathrm{3}{b}+\mathrm{3}\sqrt{\mathrm{1}−{b}^{\mathrm{4}} }\:−{b}\right) \\ $$$$=\frac{{b}^{\mathrm{2}} }{\mathrm{6}}×\left(\mathrm{2}{b}+\mathrm{3}\sqrt{\mathrm{1}−{b}^{\mathrm{4}} }\:\right) \\ $$$$\frac{{dA}}{{db}}=\frac{{b}^{\mathrm{2}} }{\mathrm{6}}×\left\{\mathrm{2}+\frac{\mathrm{3}×−\mathrm{4}{b}^{\mathrm{3}} }{\mathrm{2}\sqrt{\mathrm{1}−{b}^{\mathrm{4}} }\:}\right\}+\frac{\mathrm{2}{b}}{\mathrm{6}}\left(\mathrm{2}{b}+\mathrm{3}\sqrt{\mathrm{1}−{b}^{\mathrm{4}} }\:\right) \\ $$$$\mathrm{0}={b}\left\{\mathrm{2}−\frac{\mathrm{6}{b}^{\mathrm{3}} }{\:\sqrt{\mathrm{1}−{b}^{\mathrm{4}} }\:}\right\}+\mathrm{4}{b}+\mathrm{6}\sqrt{\mathrm{1}−{b}^{\mathrm{4}} }\: \\ $$$$\mathrm{0}=\frac{\mathrm{2}{b}\sqrt{\mathrm{1}−{b}^{\mathrm{4}} }\:−\mathrm{6}{b}^{\mathrm{4}} +\mathrm{4}{b}\sqrt{\mathrm{1}−{b}^{\mathrm{4}} }\:+\mathrm{6}\left(\mathrm{1}−{b}^{\mathrm{4}} \right)}{} \\ $$$$\mathrm{6}{b}\sqrt{\mathrm{1}−{b}^{\mathrm{4}} }\:−\mathrm{12}{b}^{\mathrm{4}} +\mathrm{6}=\mathrm{0} \\ $$$${b}\sqrt{\mathrm{1}−{b}^{\mathrm{4}} }\:−\mathrm{2}{b}^{\mathrm{4}} +\mathrm{1}=\mathrm{0} \\ $$$${b}^{\mathrm{2}} \left(\mathrm{1}−{b}^{\mathrm{4}} \right)=\mathrm{4}{b}^{\mathrm{8}} −\mathrm{4}{b}^{\mathrm{4}} +\mathrm{1} \\ $$$$\mathrm{4}{b}^{\mathrm{8}} +{b}^{\mathrm{6}} −\mathrm{4}{b}^{\mathrm{4}} −{b}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${to}\:{find}\:{b}…{wait}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by ajfour last updated on 12/Dec/18
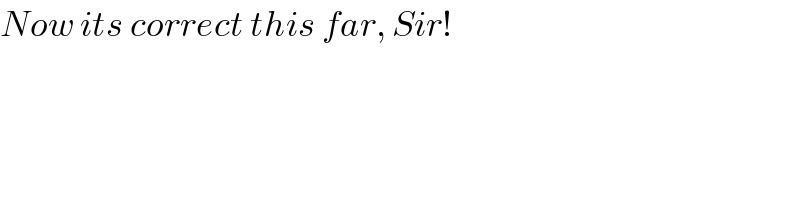
Now its correct this far, Sir!
$${Now}\:{its}\:{correct}\:{this}\:{far},\:{Sir}! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 12/Dec/18
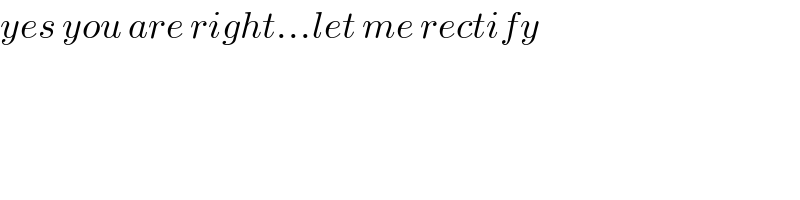
yes you are right...let me rectify
$${yes}\:{you}\:{are}\:{right}…{let}\:{me}\:{rectify} \\ $$
Commented by MJS last updated on 12/Dec/18
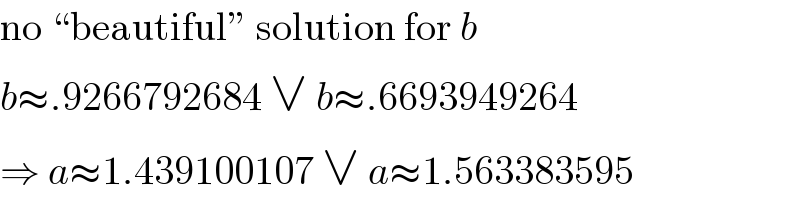
no “beautiful” solution for b b≈.9266792684 ∨ b≈.6693949264 ⇒ a≈1.439100107 ∨ a≈1.563383595
$$\mathrm{no}\:“\mathrm{beautiful}''\:\mathrm{solution}\:\mathrm{for}\:{b} \\ $$$${b}\approx.\mathrm{9266792684}\:\vee\:{b}\approx.\mathrm{6693949264} \\ $$$$\Rightarrow\:{a}\approx\mathrm{1}.\mathrm{439100107}\:\vee\:{a}\approx\mathrm{1}.\mathrm{563383595} \\ $$
Answered by mr W last updated on 12/Dec/18
eqn. of parabola: y=cx^2 with c=1 from (h,k) to (a,0): k=ch^2 (a−h)^2 +k^2 =l^2 a^2 −2ah+h^2 +c^2 h^4 =l^2 2a(da/dh)−2h(da/dh)−2a+2h+4c^2 h^3 =0 ⇒(da/dh)=1−((2c^2 h^3 )/(a−h)) A=((hk)/3)+(((a−h)k)/2)=(1/6)(3a−h)ch^2 ((d(6A/c))/dh)=2h(3a−h)+h^2 (3(da/dh)−1)=0 2(3a−h)+h(3(da/dh)−1)=0 ((2a)/h)+(da/dh)−1=0 ((2a)/h)−((2c^2 h^3 )/(a−h))=0 (a/h)=((c^2 h^3 )/(a−h)) a^2 −ha−c^2 h^4 =0 ⇒a=(h/2)[1+(√(1+(2ch)^2 ))] a^2 −2ah+h^2 +c^2 h^4 =l^2 4c^2 h^4 +h^2 [1−(√(1+(2ch)^2 ))]=2l^2 4c^2 h^2 +1−(√(1+(2ch)^2 ))=((8c^2 l^2 )/(4c^2 h^2 )) with λ=(2ch)^2 1+λ−(√(1+λ))=((8c^2 l^2 )/λ) with c=1, l=1 1+λ−(√(1+λ))=(8/λ) let t=(√(1+λ)) (t^2 −1)(t^2 −t)=8 t^4 −t^3 −t^2 +t−8=0 ⇒λ=3.4349 ⇒h=((√λ)/2)=0.9267 ⇒a=((0.9267)/2)[1+(√(1+3.4349))]=1.4391 ⇒A=(1/6)(3×1.4391−0.9267)×0.9267^2 =0.4853
$${eqn}.\:{of}\:{parabola}:\:{y}={cx}^{\mathrm{2}} \:{with}\:{c}=\mathrm{1} \\ $$$${from}\:\left({h},{k}\right)\:{to}\:\left({a},\mathrm{0}\right): \\ $$$${k}={ch}^{\mathrm{2}} \\ $$$$\left({a}−{h}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} ={l}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} −\mathrm{2}{ah}+{h}^{\mathrm{2}} +{c}^{\mathrm{2}} {h}^{\mathrm{4}} ={l}^{\mathrm{2}} \\ $$$$\mathrm{2}{a}\frac{{da}}{{dh}}−\mathrm{2}{h}\frac{{da}}{{dh}}−\mathrm{2}{a}+\mathrm{2}{h}+\mathrm{4}{c}^{\mathrm{2}} {h}^{\mathrm{3}} =\mathrm{0} \\ $$$$\Rightarrow\frac{{da}}{{dh}}=\mathrm{1}−\frac{\mathrm{2}{c}^{\mathrm{2}} {h}^{\mathrm{3}} }{{a}−{h}} \\ $$$$ \\ $$$${A}=\frac{{hk}}{\mathrm{3}}+\frac{\left({a}−{h}\right){k}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{3}{a}−{h}\right){ch}^{\mathrm{2}} \\ $$$$\frac{{d}\left(\mathrm{6}{A}/{c}\right)}{{dh}}=\mathrm{2}{h}\left(\mathrm{3}{a}−{h}\right)+{h}^{\mathrm{2}} \left(\mathrm{3}\frac{{da}}{{dh}}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{2}\left(\mathrm{3}{a}−{h}\right)+{h}\left(\mathrm{3}\frac{{da}}{{dh}}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\frac{\mathrm{2}{a}}{{h}}+\frac{{da}}{{dh}}−\mathrm{1}=\mathrm{0} \\ $$$$\frac{\mathrm{2}{a}}{{h}}−\frac{\mathrm{2}{c}^{\mathrm{2}} {h}^{\mathrm{3}} }{{a}−{h}}=\mathrm{0} \\ $$$$\frac{{a}}{{h}}=\frac{{c}^{\mathrm{2}} {h}^{\mathrm{3}} }{{a}−{h}} \\ $$$${a}^{\mathrm{2}} −{ha}−{c}^{\mathrm{2}} {h}^{\mathrm{4}} =\mathrm{0} \\ $$$$\Rightarrow{a}=\frac{{h}}{\mathrm{2}}\left[\mathrm{1}+\sqrt{\mathrm{1}+\left(\mathrm{2}{ch}\right)^{\mathrm{2}} }\right] \\ $$$$ \\ $$$${a}^{\mathrm{2}} −\mathrm{2}{ah}+{h}^{\mathrm{2}} +{c}^{\mathrm{2}} {h}^{\mathrm{4}} ={l}^{\mathrm{2}} \\ $$$$\mathrm{4}{c}^{\mathrm{2}} {h}^{\mathrm{4}} +{h}^{\mathrm{2}} \left[\mathrm{1}−\sqrt{\mathrm{1}+\left(\mathrm{2}{ch}\right)^{\mathrm{2}} }\right]=\mathrm{2}{l}^{\mathrm{2}} \\ $$$$\mathrm{4}{c}^{\mathrm{2}} {h}^{\mathrm{2}} +\mathrm{1}−\sqrt{\mathrm{1}+\left(\mathrm{2}{ch}\right)^{\mathrm{2}} }=\frac{\mathrm{8}{c}^{\mathrm{2}} {l}^{\mathrm{2}} }{\mathrm{4}{c}^{\mathrm{2}} {h}^{\mathrm{2}} } \\ $$$${with}\:\lambda=\left(\mathrm{2}{ch}\right)^{\mathrm{2}} \\ $$$$\mathrm{1}+\lambda−\sqrt{\mathrm{1}+\lambda}=\frac{\mathrm{8}{c}^{\mathrm{2}} {l}^{\mathrm{2}} }{\lambda} \\ $$$${with}\:{c}=\mathrm{1},\:{l}=\mathrm{1} \\ $$$$\mathrm{1}+\lambda−\sqrt{\mathrm{1}+\lambda}=\frac{\mathrm{8}}{\lambda} \\ $$$${let}\:{t}=\sqrt{\mathrm{1}+\lambda} \\ $$$$\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left({t}^{\mathrm{2}} −{t}\right)=\mathrm{8} \\ $$$${t}^{\mathrm{4}} −{t}^{\mathrm{3}} −{t}^{\mathrm{2}} +{t}−\mathrm{8}=\mathrm{0} \\ $$$$\Rightarrow\lambda=\mathrm{3}.\mathrm{4349} \\ $$$$\Rightarrow{h}=\frac{\sqrt{\lambda}}{\mathrm{2}}=\mathrm{0}.\mathrm{9267} \\ $$$$\Rightarrow{a}=\frac{\mathrm{0}.\mathrm{9267}}{\mathrm{2}}\left[\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{3}.\mathrm{4349}}\right]=\mathrm{1}.\mathrm{4391} \\ $$$$\Rightarrow{A}=\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{3}×\mathrm{1}.\mathrm{4391}−\mathrm{0}.\mathrm{9267}\right)×\mathrm{0}.\mathrm{9267}^{\mathrm{2}} =\mathrm{0}.\mathrm{4853} \\ $$
Commented by ajfour last updated on 12/Dec/18
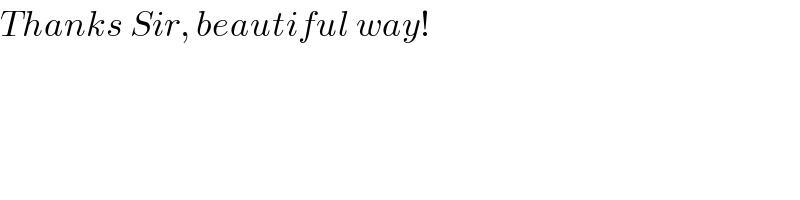
Thanks Sir, beautiful way!
$${Thanks}\:{Sir},\:{beautiful}\:{way}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *