Question Number 49964 by ajfour last updated on 12/Dec/18
Commented by ajfour last updated on 12/Dec/18
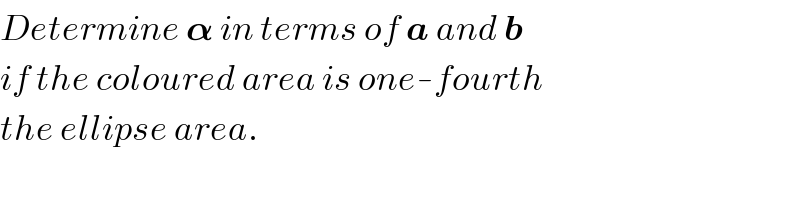
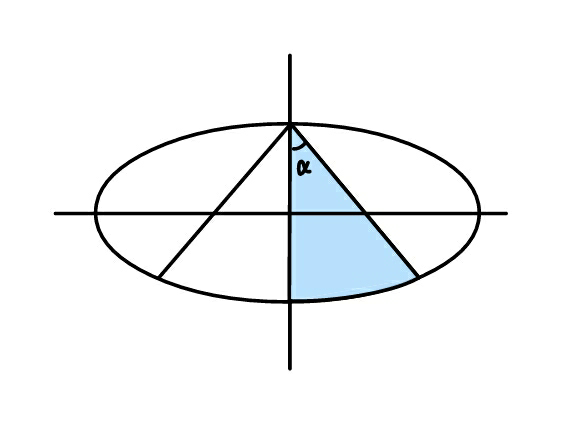
$${Determine}\:\boldsymbol{\alpha}\:{in}\:{terms}\:{of}\:\boldsymbol{{a}}\:{and}\:\boldsymbol{{b}} \\ $$$${if}\:{the}\:{coloured}\:{area}\:{is}\:{one}-{fourth} \\ $$$${the}\:{ellipse}\:{area}. \\ $$
Commented by MJS last updated on 13/Dec/18
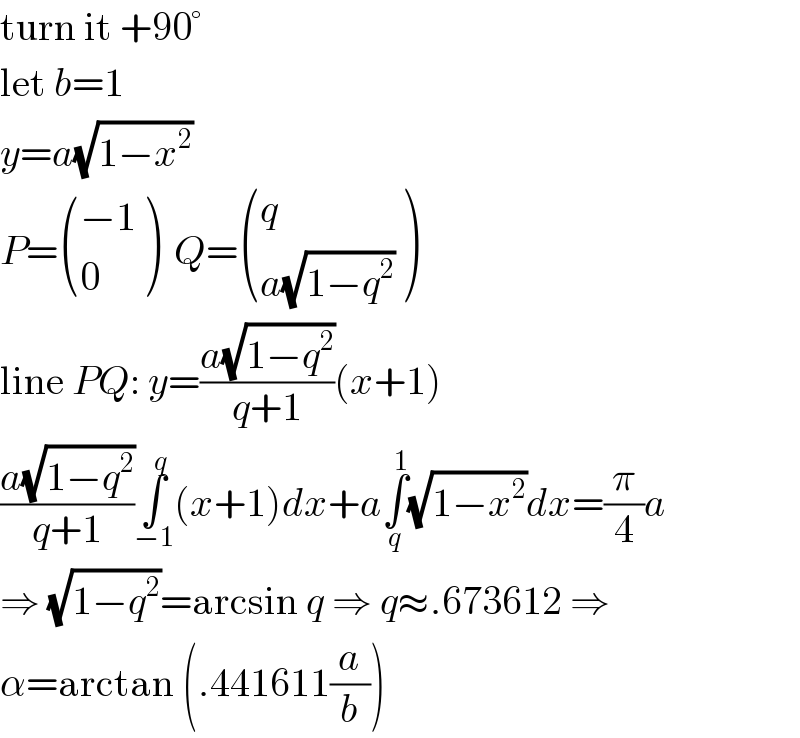
$$\mathrm{turn}\:\mathrm{it}\:+\mathrm{90}° \\ $$$$\mathrm{let}\:{b}=\mathrm{1} \\ $$$${y}={a}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${P}=\begin{pmatrix}{−\mathrm{1}}\\{\mathrm{0}}\end{pmatrix}\:\:{Q}=\begin{pmatrix}{{q}}\\{{a}\sqrt{\mathrm{1}−{q}^{\mathrm{2}} }}\end{pmatrix} \\ $$$$\mathrm{line}\:{PQ}:\:{y}=\frac{{a}\sqrt{\mathrm{1}−{q}^{\mathrm{2}} }}{{q}+\mathrm{1}}\left({x}+\mathrm{1}\right) \\ $$$$\frac{{a}\sqrt{\mathrm{1}−{q}^{\mathrm{2}} }}{{q}+\mathrm{1}}\underset{−\mathrm{1}} {\overset{{q}} {\int}}\left({x}+\mathrm{1}\right){dx}+{a}\underset{{q}} {\overset{\mathrm{1}} {\int}}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx}=\frac{\pi}{\mathrm{4}}{a} \\ $$$$\Rightarrow\:\sqrt{\mathrm{1}−{q}^{\mathrm{2}} }=\mathrm{arcsin}\:{q}\:\Rightarrow\:{q}\approx.\mathrm{673612}\:\Rightarrow \\ $$$$\alpha=\mathrm{arctan}\:\left(.\mathrm{441611}\frac{{a}}{{b}}\right) \\ $$
Answered by mr W last updated on 13/Dec/18
![y−b=−(x/(tan α))=−kx r sin θ−b=−kr cos θ r=(b/(sin θ+k cos θ)) r^2 (((cos^2 θ)/a^2 )+((sin^2 θ)/b^2 ))=1 r^2 =((a^2 b^2 )/(a^2 sin^2 θ+b^2 cos^2 θ))=(b^2 /(sin^2 θ+λ^2 cos^2 θ)) with λ=(b/a) (b^2 /((sin θ+k cos θ)^2 ))=(b^2 /(sin^2 θ+λ^2 cos^2 θ)) (1/((tan θ+k)^2 ))=(1/(tan^2 θ+λ^2 )) ⇒tan^2 θ+2k tan θ+k^2 =tan^2 θ+λ^2 ⇒tan θ_1 =((λ^2 −k^2 )/(2k)) ⇒θ_1 =tan^(−1) ((λ^2 −k^2 )/(2k)) ∫_θ_1 ^(π/2) (1/2)[(b^2 /(sin^2 θ+λ^2 cos^2 θ))−(b^2 /((sin θ+k cos θ)^2 ))]dθ=((πab)/4) ∫_θ_1 ^(π/2) [(1/(sin^2 θ+λ^2 cos^2 θ))−(1/((sin θ+k cos θ)^2 ))]dθ=(π/(2λ)) [(1/λ) tan^(−1) ((tan θ)/λ)+(1/(k+tan θ))]_θ_1 ^(π/2) =(π/(2λ)) [(1/λ)((π/2)−tan^(−1) ((λ^2 −k^2 )/(2λk)))−(1/(k+((λ^2 −k^2 )/(2k))))]=(π/(2λ)) [(1/λ)((π/2)−tan^(−1) ((λ^2 −k^2 )/(2λk)))−((2k)/(λ^2 +k^2 ))]=(π/(2λ)) tan^(−1) ((k^2 −λ^2 )/(2λk))=((2λk)/(k^2 +λ^2 )) tan^(−1) ((2λk)/(k^2 −λ^2 ))+((2λk)/(k^2 +λ^2 ))=(π/2) with μ=(k/λ) tan^(−1) (2/(μ−(1/μ)))+(2/(μ+(1/μ)))=(π/2) ⇒μ=(k/λ)=2.2644 ⇒k=(1/(tan α))=2.2644λ=2.2644(b/a) ⇒α=tan^(−1) ((0.4416a)/b)](https://www.tinkutara.com/question/Q50031.png)
$${y}−{b}=−\frac{{x}}{\mathrm{tan}\:\alpha}=−{kx} \\ $$$${r}\:\mathrm{sin}\:\theta−{b}=−{kr}\:\mathrm{cos}\:\theta \\ $$$${r}=\frac{{b}}{\mathrm{sin}\:\theta+{k}\:\mathrm{cos}\:\theta} \\ $$$${r}^{\mathrm{2}} \left(\frac{\mathrm{cos}^{\mathrm{2}} \:\theta}{{a}^{\mathrm{2}} }+\frac{\mathrm{sin}^{\mathrm{2}} \:\theta}{{b}^{\mathrm{2}} }\right)=\mathrm{1} \\ $$$${r}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}=\frac{{b}^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \:\theta+\lambda^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$${with}\:\lambda=\frac{{b}}{{a}} \\ $$$$\frac{{b}^{\mathrm{2}} }{\left(\mathrm{sin}\:\theta+{k}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} }=\frac{{b}^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \:\theta+\lambda^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{tan}\:\theta+{k}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\theta+\lambda^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{tan}^{\mathrm{2}} \:\theta+\mathrm{2}{k}\:\mathrm{tan}\:\theta+{k}^{\mathrm{2}} =\mathrm{tan}^{\mathrm{2}} \:\theta+\lambda^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{tan}\:\theta_{\mathrm{1}} =\frac{\lambda^{\mathrm{2}} −{k}^{\mathrm{2}} }{\mathrm{2}{k}} \\ $$$$\Rightarrow\theta_{\mathrm{1}} =\mathrm{tan}^{−\mathrm{1}} \frac{\lambda^{\mathrm{2}} −{k}^{\mathrm{2}} }{\mathrm{2}{k}} \\ $$$$\int_{\theta_{\mathrm{1}} } ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{b}^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \:\theta+\lambda^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta}−\frac{{b}^{\mathrm{2}} }{\left(\mathrm{sin}\:\theta+{k}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} }\right]{d}\theta=\frac{\pi{ab}}{\mathrm{4}} \\ $$$$\int_{\theta_{\mathrm{1}} } ^{\frac{\pi}{\mathrm{2}}} \left[\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:\theta+\lambda^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta}−\frac{\mathrm{1}}{\left(\mathrm{sin}\:\theta+{k}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} }\right]{d}\theta=\frac{\pi}{\mathrm{2}\lambda} \\ $$$$\left[\frac{\mathrm{1}}{\lambda}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{tan}\:\theta}{\lambda}+\frac{\mathrm{1}}{{k}+\mathrm{tan}\:\theta}\right]_{\theta_{\mathrm{1}} } ^{\frac{\pi}{\mathrm{2}}} =\frac{\pi}{\mathrm{2}\lambda} \\ $$$$\left[\frac{\mathrm{1}}{\lambda}\left(\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \frac{\lambda^{\mathrm{2}} −{k}^{\mathrm{2}} }{\mathrm{2}\lambda{k}}\right)−\frac{\mathrm{1}}{{k}+\frac{\lambda^{\mathrm{2}} −{k}^{\mathrm{2}} }{\mathrm{2}{k}}}\right]=\frac{\pi}{\mathrm{2}\lambda} \\ $$$$\left[\frac{\mathrm{1}}{\lambda}\left(\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \frac{\lambda^{\mathrm{2}} −{k}^{\mathrm{2}} }{\mathrm{2}\lambda{k}}\right)−\frac{\mathrm{2}{k}}{\lambda^{\mathrm{2}} +{k}^{\mathrm{2}} }\right]=\frac{\pi}{\mathrm{2}\lambda} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \frac{{k}^{\mathrm{2}} −\lambda^{\mathrm{2}} }{\mathrm{2}\lambda{k}}=\frac{\mathrm{2}\lambda{k}}{{k}^{\mathrm{2}} +\lambda^{\mathrm{2}} } \\ $$$$\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}\lambda{k}}{{k}^{\mathrm{2}} −\lambda^{\mathrm{2}} }+\frac{\mathrm{2}\lambda{k}}{{k}^{\mathrm{2}} +\lambda^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}} \\ $$$${with}\:\mu=\frac{{k}}{\lambda} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}}{\mu−\frac{\mathrm{1}}{\mu}}+\frac{\mathrm{2}}{\mu+\frac{\mathrm{1}}{\mu}}=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\mu=\frac{{k}}{\lambda}=\mathrm{2}.\mathrm{2644} \\ $$$$\Rightarrow{k}=\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}=\mathrm{2}.\mathrm{2644}\lambda=\mathrm{2}.\mathrm{2644}\frac{{b}}{{a}} \\ $$$$\Rightarrow\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{0}.\mathrm{4416}{a}}{{b}} \\ $$
Commented by mr W last updated on 13/Dec/18
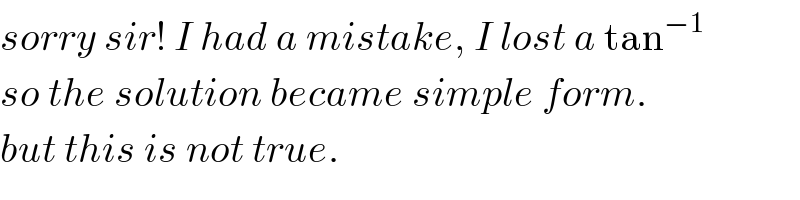
$${sorry}\:{sir}!\:{I}\:{had}\:{a}\:{mistake},\:{I}\:{lost}\:{a}\:\mathrm{tan}^{−\mathrm{1}} \\ $$$${so}\:{the}\:{solution}\:{became}\:{simple}\:{form}.\: \\ $$$${but}\:{this}\:{is}\:{not}\:{true}. \\ $$
Commented by MJS last updated on 13/Dec/18
$$\mathrm{this}\:\mathrm{is}\:\mathrm{different}\:\mathrm{from}\:\mathrm{my}\:\mathrm{solution}… \\ $$$$\mathrm{please}\:\mathrm{check}\:\mathrm{mine} \\ $$
Commented by MJS last updated on 13/Dec/18

$$\mathrm{ok}.\:\mathrm{I}\:\mathrm{also}\:\mathrm{went}\:\mathrm{through}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{but} \\ $$$$\mathrm{couldn}'\mathrm{t}\:\mathrm{find}\:\mathrm{a}\:\mathrm{mistake}.\:\mathrm{thank}\:\mathrm{you}\:\mathrm{for} \\ $$$$\mathrm{checking}! \\ $$
Commented by mr W last updated on 13/Dec/18
$${now}\:{we}\:{have}\:{the}\:{same}\:{result}. \\ $$
Commented by ajfour last updated on 13/Dec/18
$${Congratulations}\:{and}\:{thanks}\: \\ $$$${to}\:{both}\:{Sirs}. \\ $$
