Question-49970

Question Number 49970 by behi83417@gmail.com last updated on 12/Dec/18

Commented by behi83417@gmail.com last updated on 12/Dec/18

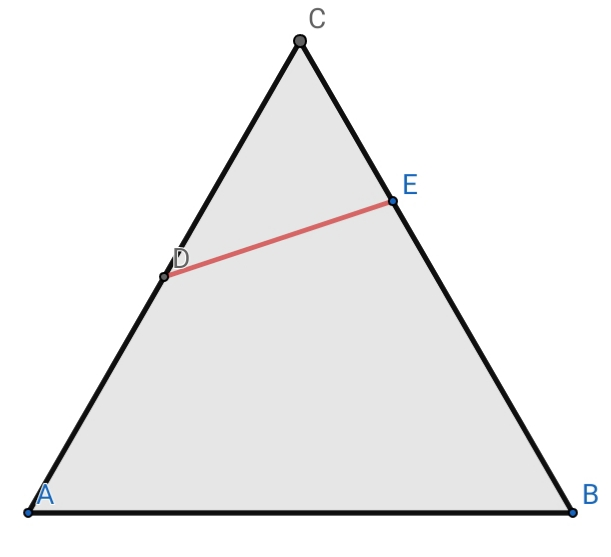
$${ABC},{equilateral}.{AD}={DC},\measuredangle{CDE}=\mathrm{30}^{\bullet} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\frac{{area}\left[{ABED}\right]}{{area}\left[{EDC}\right]}=? \\ $$

Answered by mr W last updated on 12/Dec/18

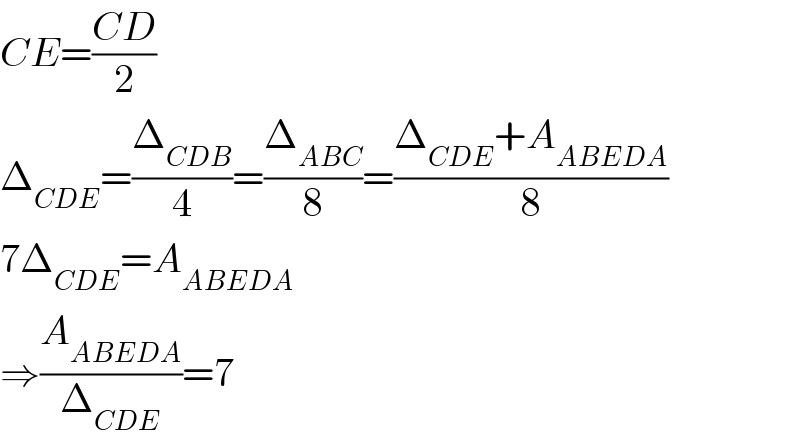
$${CE}=\frac{{CD}}{\mathrm{2}} \\ $$$$\Delta_{{CDE}} =\frac{\Delta_{{CDB}} }{\mathrm{4}}=\frac{\Delta_{{ABC}} }{\mathrm{8}}=\frac{\Delta_{{CDE}} +{A}_{{ABEDA}} }{\mathrm{8}} \\ $$$$\mathrm{7}\Delta_{{CDE}} ={A}_{{ABEDA}} \\ $$$$\Rightarrow\frac{{A}_{{ABEDA}} }{\Delta_{{CDE}} }=\mathrm{7} \\ $$

Commented by behi83417@gmail.com last updated on 12/Dec/18

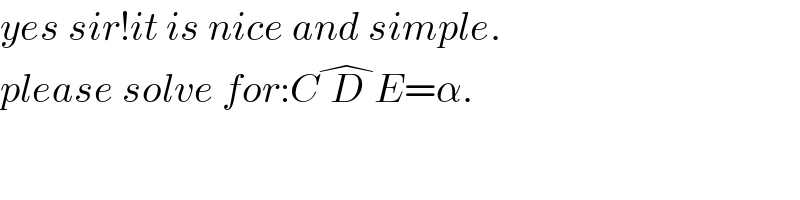
$${yes}\:{sir}!{it}\:{is}\:{nice}\:{and}\:{simple}. \\ $$$${please}\:{solve}\:{for}:{C}\overset{} {{D}E}=\alpha. \\ $$

Answered by mr W last updated on 12/Dec/18

$${AB}={a} \\ $$$$\angle{CDE}=\alpha \\ $$$$\frac{{CE}}{\mathrm{sin}\:\alpha}=\frac{{a}}{\mathrm{2}\:\mathrm{sin}\:\left(\alpha+\frac{\pi}{\mathrm{3}}\right)}=\frac{{a}}{\mathrm{sin}\:\alpha+\sqrt{\mathrm{3}}\:\mathrm{cos}\:\alpha} \\ $$$$\Rightarrow{CE}=\frac{{a}}{\mathrm{1}+\sqrt{\mathrm{3}}\:\mathrm{cot}\:\alpha} \\ $$$$\Delta{CBE}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{{a}}{\mathrm{2}}×\frac{{a}}{\mathrm{1}+\sqrt{\mathrm{3}}\:\mathrm{cot}\:\alpha}×\mathrm{sin}\:\frac{\pi}{\mathrm{3}} \\ $$$$\Delta{CBE}=\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{8}\left(\sqrt{\mathrm{3}}+\mathrm{3}\:\mathrm{cot}\:\alpha\right)} \\ $$$$\Delta_{{ABC}} =\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\frac{\Delta_{{ABC}} }{\Delta_{{CBE}} }=\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\:\mathrm{cot}\:\alpha\right) \\ $$$$\Rightarrow\frac{{A}_{{ABED}} }{\Delta_{{CBE}} }=\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{cot}\:\alpha \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com