Question Number 49984 by behi83417@gmail.com last updated on 12/Dec/18

Commented by behi83417@gmail.com last updated on 12/Dec/18

$${A}\overset{\bigtriangleup} {{B}C},{equilateral}.{AB}={a},{A}\overset{�} {{C}E}=\alpha. \\ $$$${find}:{AD},{BD},{in}\:{terms}\:{of}\:{a}\:{and}\:\:\alpha. \\ $$
Answered by mr W last updated on 12/Dec/18
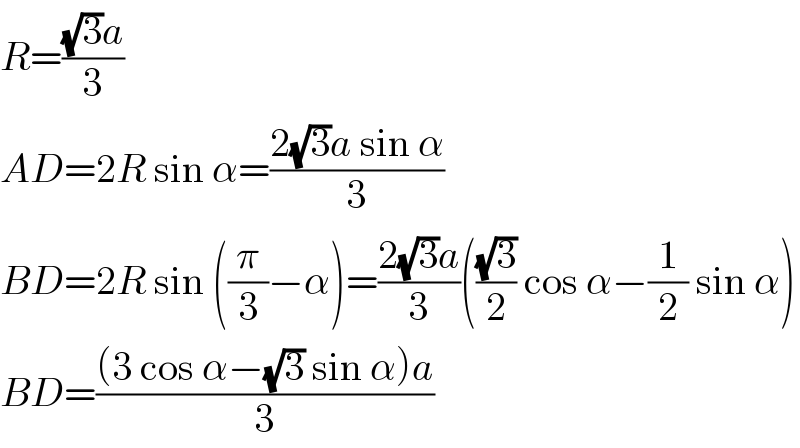
$${R}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{3}} \\ $$$${AD}=\mathrm{2}{R}\:\mathrm{sin}\:\alpha=\frac{\mathrm{2}\sqrt{\mathrm{3}}{a}\:\mathrm{sin}\:\alpha}{\mathrm{3}} \\ $$$${BD}=\mathrm{2}{R}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\alpha\right)=\frac{\mathrm{2}\sqrt{\mathrm{3}}{a}}{\mathrm{3}}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{cos}\:\alpha−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{sin}\:\alpha\right) \\ $$$${BD}=\frac{\left(\mathrm{3}\:\mathrm{cos}\:\alpha−\sqrt{\mathrm{3}}\:\mathrm{sin}\:\alpha\right){a}}{\mathrm{3}} \\ $$
