Menu Close

Question-49987

Tinku Tara 0 Comments
Pin




Question Number 49987 by ajfour last updated on 12/Dec/18
Commented by ajfour last updated on 12/Dec/18
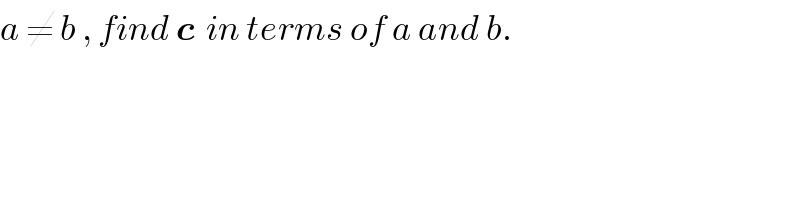
a ≠ b , find c in terms of a and b.
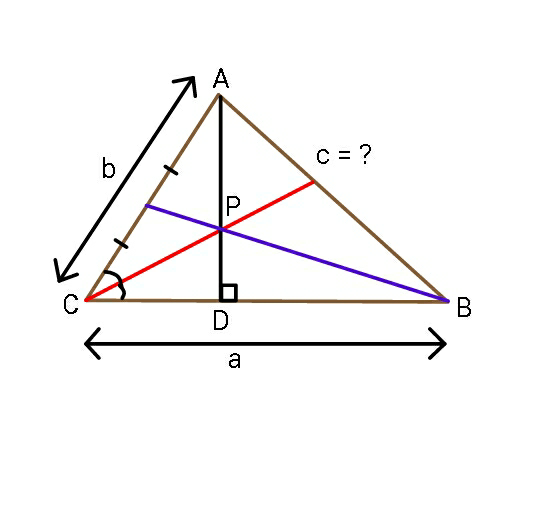
$${a}\:\neq\:{b}\:,\:{find}\:\boldsymbol{{c}}\:\:{in}\:{terms}\:{of}\:{a}\:{and}\:{b}. \\ $$
Commented by MJS last updated on 13/Dec/18
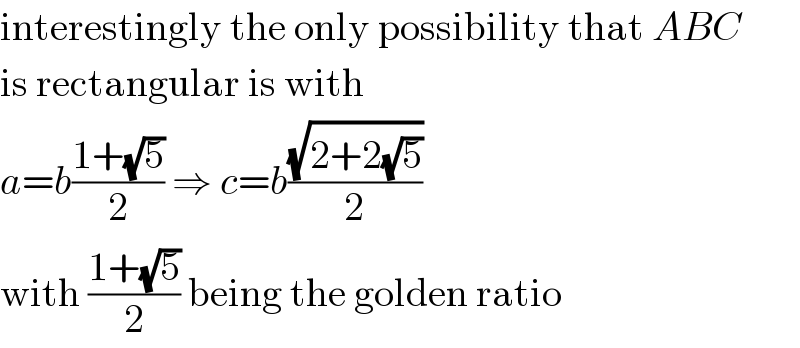
interestingly the only possibility that ABC is rectangular is with a=b((1+(√5))/2) ⇒ c=b((√(2+2(√5)))/2) with ((1+(√5))/2) being the golden ratio
$$\mathrm{interestingly}\:\mathrm{the}\:\mathrm{only}\:\mathrm{possibility}\:\mathrm{that}\:{ABC} \\ $$$$\mathrm{is}\:\mathrm{rectangular}\:\mathrm{is}\:\mathrm{with} \\ $$$${a}={b}\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\Rightarrow\:{c}={b}\frac{\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{2}} \\ $$$$\mathrm{with}\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\mathrm{being}\:\mathrm{the}\:\mathrm{golden}\:\mathrm{ratio} \\ $$
Commented by ajfour last updated on 13/Dec/18
how to get (a/b) Sir ?
$${how}\:{to}\:{get}\:\frac{{a}}{{b}}\:{Sir}\:? \\ $$
Commented by MJS last updated on 13/Dec/18
let b=1 for calculation.
$$\mathrm{let}\:{b}=\mathrm{1}\:\mathrm{for}\:\mathrm{calculation}. \\ $$
Answered by mr W last updated on 13/Dec/18
C(0,0), B(a,0), A(b cos 2θ,b sin 2θ) Q=midpoint AC Q((b/2) cos 2θ, (b/2) sin 2θ) eqn. BQ: (y/((b/2) sin 2θ))=((x−a)/((b/2)cos 2θ−a)) (y_P /((b/2) sin 2θ))=((b cos 2θ−a)/((b/2)cos 2θ−a)) ⇒y_P =((b sin 2θ (b cos 2θ−a))/(b cos 2θ−2a)) y_P =b cos 2θ tan θ ⇒((b sin 2θ (b cos 2θ−a))/(b cos 2θ−2a))=b cos 2θ tan θ ⇒((tan 2θ (b cos 2θ−a))/(b cos 2θ−2a))=tan θ with λ=(a/b), μ=cos 2θ ⇒((tan 2θ (cos 2θ−λ))/(cos 2θ−2λ))=tan θ=(√((1−cos 2θ)/(1+cos 2θ))) ⇒(((√(1−cos^2 2θ))(cos 2θ−λ))/(cos 2θ(cos 2θ−2λ)))=(√((1−cos 2θ)/(1+cos 2θ))) ⇒(((μ−λ))/(μ(μ−2λ)))=(1/(1+μ)) (1+μ)(μ−λ)=μ(μ−2λ) (1+λ)μ=λ ⇒μ=(λ/(1+λ))=(a/(a+b)) c^2 =a^2 +b^2 −2ab cos 2θ=a^2 +b^2 −2abμ c^2 =a^2 +b^2 −((2a^2 b)/(a+b)) ⇒c=(√(a^2 +b^2 −((2a^2 b)/(a+b))))
$${C}\left(\mathrm{0},\mathrm{0}\right),\:{B}\left({a},\mathrm{0}\right),\:{A}\left({b}\:\mathrm{cos}\:\mathrm{2}\theta,{b}\:\mathrm{sin}\:\mathrm{2}\theta\right) \\ $$$${Q}={midpoint}\:{AC} \\ $$$${Q}\left(\frac{{b}}{\mathrm{2}}\:\mathrm{cos}\:\mathrm{2}\theta,\:\frac{{b}}{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}\theta\right) \\ $$$${eqn}.\:{BQ}: \\ $$$$\frac{{y}}{\frac{{b}}{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}\theta}=\frac{{x}−{a}}{\frac{{b}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}\theta−{a}} \\ $$$$\frac{{y}_{{P}} }{\frac{{b}}{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}\theta}=\frac{{b}\:\mathrm{cos}\:\mathrm{2}\theta−{a}}{\frac{{b}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}\theta−{a}} \\ $$$$\Rightarrow{y}_{{P}} =\frac{{b}\:\mathrm{sin}\:\mathrm{2}\theta\:\left({b}\:\mathrm{cos}\:\mathrm{2}\theta−{a}\right)}{{b}\:\mathrm{cos}\:\mathrm{2}\theta−\mathrm{2}{a}} \\ $$$${y}_{{P}} ={b}\:\mathrm{cos}\:\mathrm{2}\theta\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow\frac{{b}\:\mathrm{sin}\:\mathrm{2}\theta\:\left({b}\:\mathrm{cos}\:\mathrm{2}\theta−{a}\right)}{{b}\:\mathrm{cos}\:\mathrm{2}\theta−\mathrm{2}{a}}={b}\:\mathrm{cos}\:\mathrm{2}\theta\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow\frac{\mathrm{tan}\:\mathrm{2}\theta\:\left({b}\:\mathrm{cos}\:\mathrm{2}\theta−{a}\right)}{{b}\:\mathrm{cos}\:\mathrm{2}\theta−\mathrm{2}{a}}=\mathrm{tan}\:\theta \\ $$$${with}\:\lambda=\frac{{a}}{{b}},\:\mu=\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\Rightarrow\frac{\mathrm{tan}\:\mathrm{2}\theta\:\left(\mathrm{cos}\:\mathrm{2}\theta−\lambda\right)}{\mathrm{cos}\:\mathrm{2}\theta−\mathrm{2}\lambda}=\mathrm{tan}\:\theta=\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta}} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}\theta}\left(\mathrm{cos}\:\mathrm{2}\theta−\lambda\right)}{\mathrm{cos}\:\mathrm{2}\theta\left(\mathrm{cos}\:\mathrm{2}\theta−\mathrm{2}\lambda\right)}=\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta}} \\ $$$$\Rightarrow\frac{\left(\mu−\lambda\right)}{\mu\left(\mu−\mathrm{2}\lambda\right)}=\frac{\mathrm{1}}{\mathrm{1}+\mu} \\ $$$$\left(\mathrm{1}+\mu\right)\left(\mu−\lambda\right)=\mu\left(\mu−\mathrm{2}\lambda\right) \\ $$$$\left(\mathrm{1}+\lambda\right)\mu=\lambda \\ $$$$\Rightarrow\mu=\frac{\lambda}{\mathrm{1}+\lambda}=\frac{{a}}{{a}+{b}} \\ $$$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\mathrm{2}\theta={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\mu \\ $$$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\frac{\mathrm{2}{a}^{\mathrm{2}} {b}}{{a}+{b}} \\ $$$$\Rightarrow{c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\frac{\mathrm{2}{a}^{\mathrm{2}} {b}}{{a}+{b}}} \\ $$
Commented by ajfour last updated on 13/Dec/18
Very Nice Sir! Thanks a lot.
$${Very}\:{Nice}\:{Sir}!\:{Thanks}\:{a}\:{lot}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *