Menu Close

Question-50052

Tinku Tara 0 Comments
Pin




Question Number 50052 by cesar.marval.larez@gmail.com last updated on 13/Dec/18
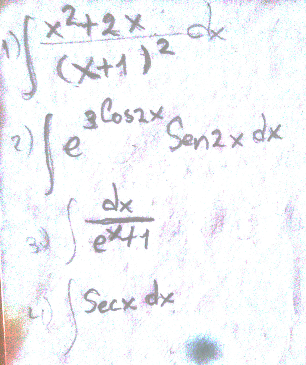
Commented by maxmathsup by imad last updated on 13/Dec/18
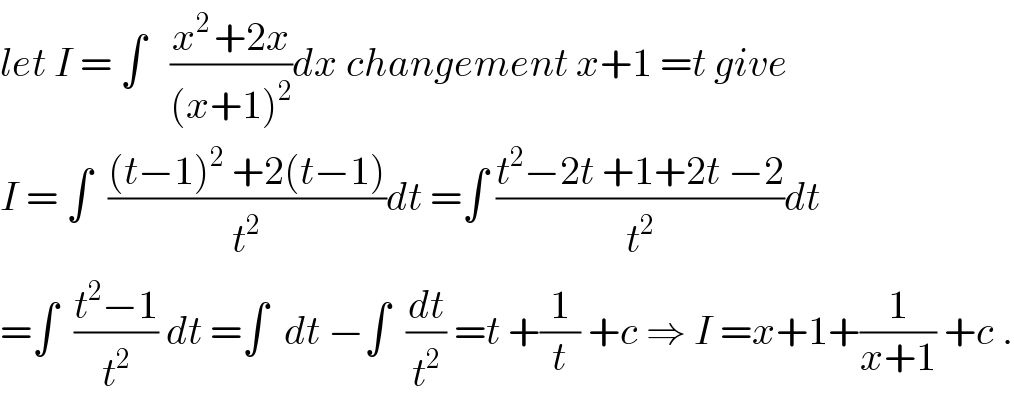
let I = ∫ ((x^(2 ) +2x)/((x+1)^2 ))dx changement x+1 =t give I = ∫ (((t−1)^2 +2(t−1))/t^2 )dt =∫ ((t^2 −2t +1+2t −2)/t^2 )dt =∫ ((t^2 −1)/t^2 ) dt =∫ dt −∫ (dt/t^2 ) =t +(1/t) +c ⇒ I =x+1+(1/(x+1)) +c .
$${let}\:{I}\:=\:\int\:\:\:\frac{{x}^{\mathrm{2}\:} +\mathrm{2}{x}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:{changement}\:{x}+\mathrm{1}\:={t}\:{give} \\ $$$${I}\:=\:\int\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{2}\left({t}−\mathrm{1}\right)}{{t}^{\mathrm{2}} }{dt}\:=\int\:\frac{{t}^{\mathrm{2}} −\mathrm{2}{t}\:+\mathrm{1}+\mathrm{2}{t}\:−\mathrm{2}}{{t}^{\mathrm{2}} }{dt} \\ $$$$=\int\:\:\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} }\:{dt}\:=\int\:\:{dt}\:−\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} }\:={t}\:+\frac{\mathrm{1}}{{t}}\:+{c}\:\Rightarrow\:{I}\:={x}+\mathrm{1}+\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+{c}\:. \\ $$
Answered by peter frank last updated on 13/Dec/18
4)∫(1/(cosx))dx cosx=((1−t^2 )/(1+t^2 )) t=tan (x/2) dx=((2dt)/(1+t^2 )) ∫((2dt)/(1−t^2 ))=∫(((1−t)+(1+t))/(1−t^2 )) =ln ((1+t)/(1−t))+B ln((1+tan (x/2))/(1−tan (x/2)))=ln [((cos(x/2) +sin (x/2))/(cos (x/2)−sin (x/2)))]⇒(rationalise denominator) ln [((1+sin x)/(cos x))]+D ln [secx+tan x]+D
$$\left.\mathrm{4}\right)\int\frac{\mathrm{1}}{\mathrm{cosx}}\mathrm{dx} \\ $$$$\mathrm{cosx}=\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$\mathrm{t}=\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}} \\ $$$$\mathrm{dx}=\frac{\mathrm{2dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$\int\frac{\mathrm{2dt}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }=\int\frac{\left(\mathrm{1}−\mathrm{t}\right)+\left(\mathrm{1}+\mathrm{t}\right)}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} } \\ $$$$=\mathrm{ln}\:\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}+\mathrm{B} \\ $$$$\mathrm{ln}\frac{\mathrm{1}+\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}}=\mathrm{ln}\:\left[\frac{\mathrm{cos}\frac{\mathrm{x}}{\mathrm{2}}\:+\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}}\right]\Rightarrow\left(\mathrm{rationalise}\:\mathrm{denominator}\right) \\ $$$$\mathrm{ln}\:\left[\frac{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}}\right]+\mathrm{D} \\ $$$$\mathrm{ln}\:\left[\mathrm{secx}+\mathrm{tan}\:\mathrm{x}\right]+\mathrm{D} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 13/Dec/18
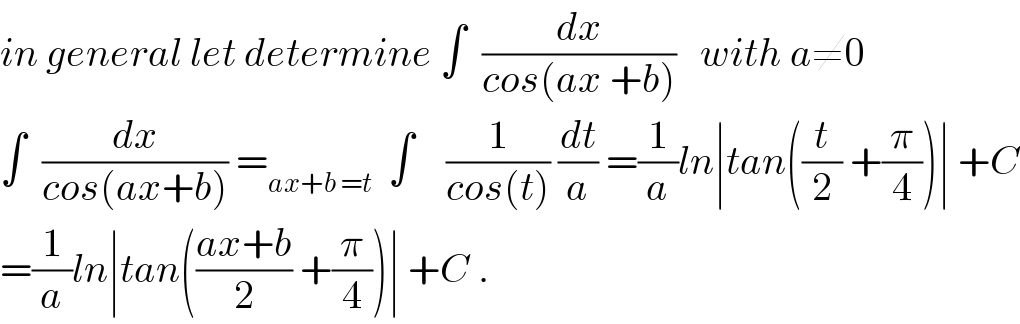
in general let determine ∫ (dx/(cos(ax +b))) with a≠0 ∫ (dx/(cos(ax+b))) =_(ax+b =t) ∫ (1/(cos(t))) (dt/a) =(1/a)ln∣tan((t/2) +(π/4))∣ +C =(1/a)ln∣tan(((ax+b)/2) +(π/4))∣ +C .
$${in}\:{general}\:{let}\:{determine}\:\int\:\:\frac{{dx}}{{cos}\left({ax}\:+{b}\right)}\:\:\:{with}\:{a}\neq\mathrm{0} \\ $$$$\int\:\:\frac{{dx}}{{cos}\left({ax}+{b}\right)}\:=_{{ax}+{b}\:={t}} \:\:\int\:\:\:\:\frac{\mathrm{1}}{{cos}\left({t}\right)}\:\frac{{dt}}{{a}}\:=\frac{\mathrm{1}}{{a}}{ln}\mid{tan}\left(\frac{{t}}{\mathrm{2}}\:+\frac{\pi}{\mathrm{4}}\right)\mid\:+{C} \\ $$$$=\frac{\mathrm{1}}{{a}}{ln}\mid{tan}\left(\frac{{ax}+{b}}{\mathrm{2}}\:+\frac{\pi}{\mathrm{4}}\right)\mid\:+{C}\:. \\ $$
Commented by $@ty@m last updated on 13/Dec/18
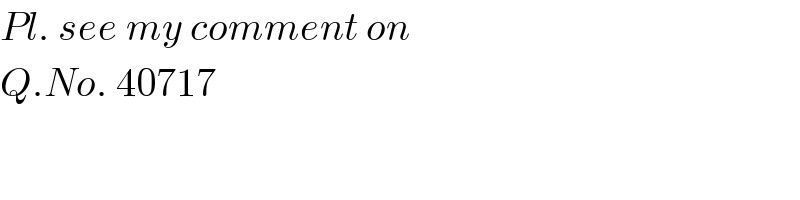
Pl. see my comment on Q.No. 40717
$${Pl}.\:{see}\:{my}\:{comment}\:{on}\: \\ $$$${Q}.{No}.\:\mathrm{40717} \\ $$
Commented by maxmathsup by imad last updated on 13/Dec/18
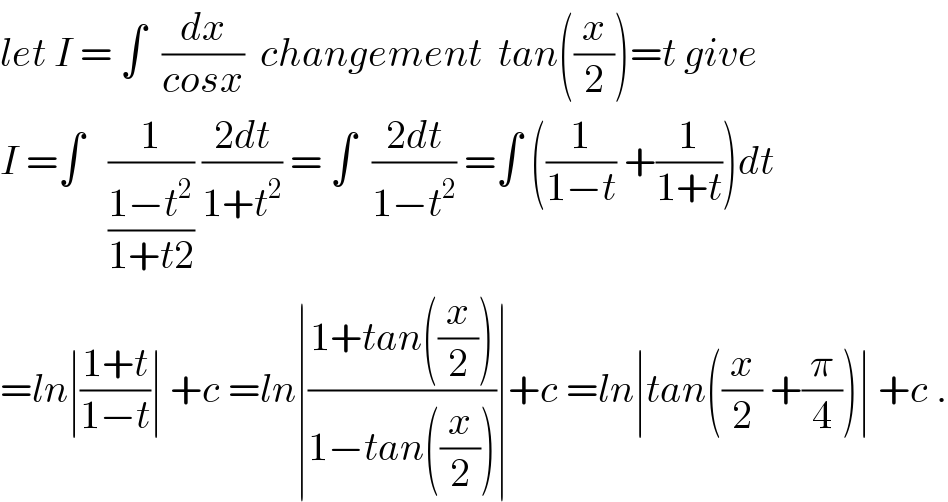
let I = ∫ (dx/(cosx)) changement tan((x/2))=t give I =∫ (1/((1−t^2 )/(1+t2))) ((2dt)/(1+t^2 )) = ∫ ((2dt)/(1−t^2 )) =∫ ((1/(1−t)) +(1/(1+t)))dt =ln∣((1+t)/(1−t))∣ +c =ln∣((1+tan((x/2)))/(1−tan((x/2))))∣+c =ln∣tan((x/2) +(π/4))∣ +c .
$${let}\:{I}\:=\:\int\:\:\frac{{dx}}{{cosx}}\:\:{changement}\:\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$${I}\:=\int\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}\mathrm{2}}}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\int\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}−{t}^{\mathrm{2}} }\:=\int\:\left(\frac{\mathrm{1}}{\mathrm{1}−{t}}\:+\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){dt} \\ $$$$={ln}\mid\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\mid\:+{c}\:={ln}\mid\frac{\mathrm{1}+{tan}\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{1}−{tan}\left(\frac{{x}}{\mathrm{2}}\right)}\mid+{c}\:={ln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\:+\frac{\pi}{\mathrm{4}}\right)\mid\:+{c}\:. \\ $$
Answered by afachri last updated on 13/Dec/18
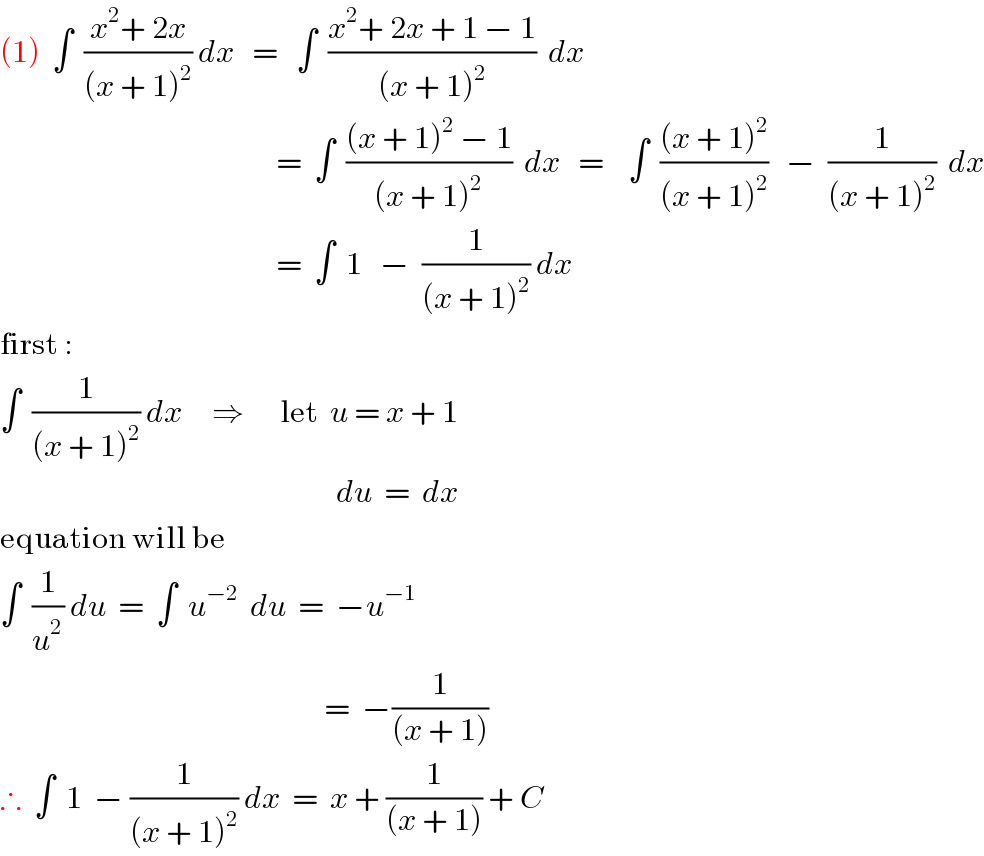
(1) ∫ ((x^2 + 2x)/((x + 1)^2 )) dx = ∫ ((x^2 + 2x + 1 − 1)/((x + 1)^2 )) dx = ∫ (((x + 1)^2 − 1)/((x + 1)^2 )) dx = ∫ (((x + 1)^2 )/((x + 1)^2 )) − (1/((x + 1)^2 )) dx = ∫ 1 − (1/((x + 1)^2 )) dx first : ∫ (1/((x + 1)^2 )) dx ⇒ let u = x + 1 du = dx equation will be ∫ (1/u^2 ) du = ∫ u^(−2) du = −u^(−1) = −(1/((x + 1))) ∴ ∫ 1 − (1/((x + 1)^2 )) dx = x + (1/((x + 1))) + C
$$\left(\mathrm{1}\right)\:\:\int\:\:\frac{{x}^{\mathrm{2}} +\:\mathrm{2}{x}}{\left({x}\:+\:\mathrm{1}\right)^{\mathrm{2}} }\:{dx}\:\:\:=\:\:\:\int\:\:\frac{{x}^{\mathrm{2}} +\:\mathrm{2}{x}\:+\:\mathrm{1}\:−\:\mathrm{1}}{\left({x}\:+\:\mathrm{1}\right)^{\mathrm{2}} }\:\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\int\:\:\frac{\left({x}\:+\:\mathrm{1}\right)^{\mathrm{2}} \:−\:\mathrm{1}}{\left({x}\:+\:\mathrm{1}\right)^{\mathrm{2}} }\:\:{dx}\:\:\:=\:\:\:\:\int\:\:\frac{\left({x}\:+\:\mathrm{1}\right)^{\mathrm{2}} }{\left({x}\:+\:\mathrm{1}\right)^{\mathrm{2}} }\:\:\:−\:\:\frac{\mathrm{1}}{\left({x}\:+\:\mathrm{1}\right)^{\mathrm{2}} }\:\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\int\:\:\mathrm{1}\:\:\:−\:\:\frac{\mathrm{1}}{\left({x}\:+\:\mathrm{1}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\mathrm{first}\:: \\ $$$$\int\:\:\frac{\mathrm{1}}{\left({x}\:+\:\mathrm{1}\right)^{\mathrm{2}} }\:{dx}\:\:\:\:\:\Rightarrow\:\:\:\:\:\:\mathrm{let}\:\:{u}\:=\:{x}\:+\:\mathrm{1}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{du}\:\:=\:\:{dx} \\ $$$$\mathrm{equation}\:\mathrm{will}\:\mathrm{be}\: \\ $$$$\int\:\:\frac{\mathrm{1}}{{u}^{\mathrm{2}} }\:{du}\:\:=\:\:\int\:\:{u}^{−\mathrm{2}} \:\:{du}\:\:=\:\:−{u}^{−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:−\frac{\mathrm{1}}{\left({x}\:+\:\mathrm{1}\right)} \\ $$$$\therefore\:\:\int\:\:\mathrm{1}\:\:−\:\frac{\mathrm{1}}{\left({x}\:+\:\mathrm{1}\right)^{\mathrm{2}} }\:{dx}\:\:=\:\:{x}\:+\:\frac{\mathrm{1}}{\left({x}\:+\:\mathrm{1}\right)}\:+\:{C} \\ $$
Answered by Joel578 last updated on 13/Dec/18
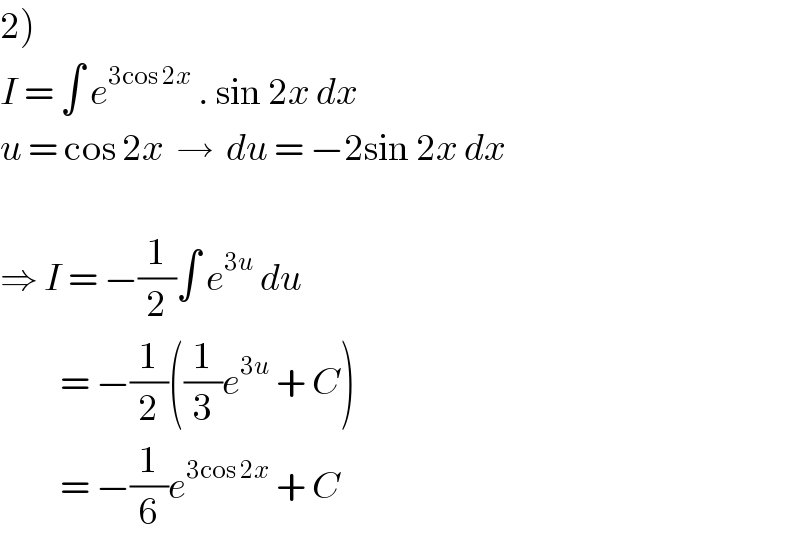
2) I = ∫ e^(3cos 2x) . sin 2x dx u = cos 2x → du = −2sin 2x dx ⇒ I = −(1/2)∫ e^(3u) du = −(1/2)((1/3)e^(3u) + C) = −(1/6)e^(3cos 2x) + C
$$\left.\mathrm{2}\right) \\ $$$${I}\:=\:\int\:{e}^{\mathrm{3cos}\:\mathrm{2}{x}} \:.\:\mathrm{sin}\:\mathrm{2}{x}\:{dx} \\ $$$${u}\:=\:\mathrm{cos}\:\mathrm{2}{x}\:\:\rightarrow\:\:{du}\:=\:−\mathrm{2sin}\:\mathrm{2}{x}\:{dx} \\ $$$$ \\ $$$$\Rightarrow\:{I}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:{e}^{\mathrm{3}{u}} \:{du} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{u}} \:+\:{C}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:−\frac{\mathrm{1}}{\mathrm{6}}{e}^{\mathrm{3cos}\:\mathrm{2}{x}} \:+\:{C} \\ $$
Answered by Joel578 last updated on 14/Dec/18
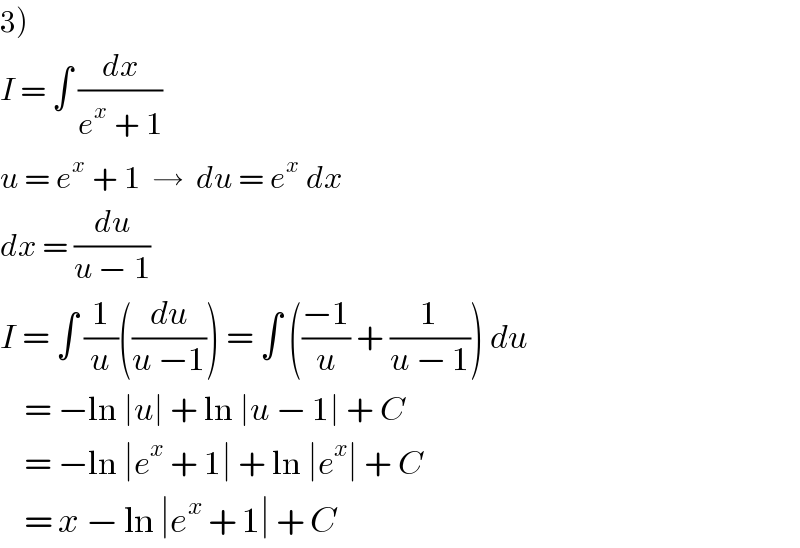
3) I = ∫ (dx/(e^x + 1)) u = e^x + 1 → du = e^x dx dx = (du/(u − 1)) I = ∫ (1/u)((du/(u −1))) = ∫ (((−1)/u) + (1/(u − 1))) du = −ln ∣u∣ + ln ∣u − 1∣ + C = −ln ∣e^x + 1∣ + ln ∣e^x ∣ + C = x − ln ∣e^x + 1∣ + C
$$\left.\mathrm{3}\right) \\ $$$${I}\:=\:\int\:\frac{{dx}}{{e}^{{x}} \:+\:\mathrm{1}} \\ $$$${u}\:=\:{e}^{{x}} \:+\:\mathrm{1}\:\:\rightarrow\:\:{du}\:=\:{e}^{{x}} \:{dx} \\ $$$${dx}\:=\:\frac{{du}}{{u}\:−\:\mathrm{1}} \\ $$$${I}\:=\:\int\:\frac{\mathrm{1}}{{u}}\left(\frac{{du}}{{u}\:−\mathrm{1}}\right)\:=\:\int\:\left(\frac{−\mathrm{1}}{{u}}\:+\:\frac{\mathrm{1}}{{u}\:−\:\mathrm{1}}\right)\:{du} \\ $$$$\:\:\:\:=\:−\mathrm{ln}\:\mid{u}\mid\:+\:\mathrm{ln}\:\mid{u}\:−\:\mathrm{1}\mid\:+\:{C} \\ $$$$\:\:\:\:=\:−\mathrm{ln}\:\mid{e}^{{x}} \:+\:\mathrm{1}\mid\:+\:\mathrm{ln}\:\mid{e}^{{x}} \mid\:+\:{C} \\ $$$$\:\:\:\:=\:{x}\:−\:\mathrm{ln}\:\mid{e}^{{x}} \:+\:\mathrm{1}\mid\:+\:{C} \\ $$
Commented by cesar.marval.larez@gmail.com last updated on 13/Dec/18
thank u everyone
$${thank}\:{u}\:{everyone}\: \\ $$
Commented by afachri last updated on 14/Dec/18
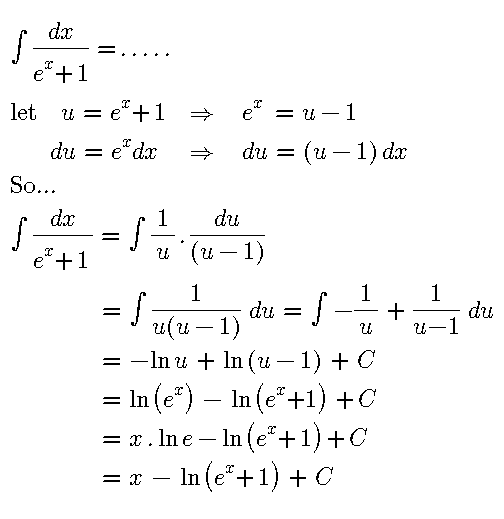
Commented by Joel578 last updated on 14/Dec/18
thank you for correction
$${thank}\:{you}\:{for}\:{correction} \\ $$
Commented by afachri last updated on 24/Dec/18
your welcome Sir
$$\mathrm{your}\:\mathrm{welcome}\:\mathrm{Sir} \\ $$
Answered by peter frank last updated on 13/Dec/18
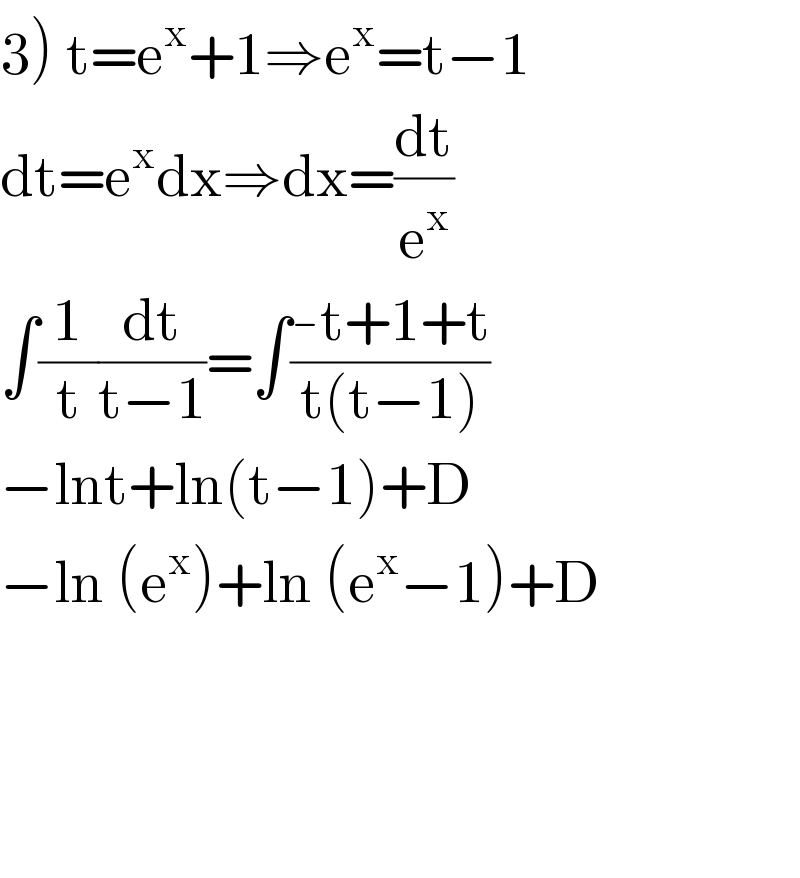
3) t=e^x +1⇒e^x =t−1 dt=e^x dx⇒dx=(dt/e^x ) ∫(1/t)(dt/(t−1))=∫((-t+1+t)/(t(t−1))) −lnt+ln(t−1)+D −ln (e^x )+ln (e^x −1)+D
$$\left.\mathrm{3}\right)\:\mathrm{t}=\mathrm{e}^{\mathrm{x}} +\mathrm{1}\Rightarrow\mathrm{e}^{\mathrm{x}} =\mathrm{t}−\mathrm{1} \\ $$$$\mathrm{dt}=\mathrm{e}^{\mathrm{x}} \mathrm{dx}\Rightarrow\mathrm{dx}=\frac{\mathrm{dt}}{\mathrm{e}^{\mathrm{x}} } \\ $$$$\int\frac{\mathrm{1}}{\mathrm{t}}\frac{\mathrm{dt}}{\mathrm{t}−\mathrm{1}}=\int\frac{-\mathrm{t}+\mathrm{1}+\mathrm{t}}{\mathrm{t}\left(\mathrm{t}−\mathrm{1}\right)} \\ $$$$−\mathrm{lnt}+\mathrm{ln}\left(\mathrm{t}−\mathrm{1}\right)+\mathrm{D} \\ $$$$−\mathrm{ln}\:\left(\mathrm{e}^{\mathrm{x}} \right)+\mathrm{ln}\:\left(\mathrm{e}^{\mathrm{x}} −\mathrm{1}\right)+\mathrm{D} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *