Question-50101

Question Number 50101 by ajfour last updated on 13/Dec/18

Commented by ajfour last updated on 14/Dec/18

If system of ring and block be released as shown, and later the ring hits the block as shown in dashed lines, determine a. Find also the velocity of ring then. Assume friction sufficient such that ring rolls purely as it moves.

$${If}\:{system}\:{of}\:{ring}\:{and}\:{block}\:{be} \\ $$$${released}\:{as}\:{shown},\:{and}\:{later}\:{the} \\ $$$${ring}\:{hits}\:{the}\:{block}\:{as}\:{shown}\:{in} \\ $$$${dashed}\:{lines},\:{determine}\:\boldsymbol{{a}}. \\ $$$${Find}\:{also}\:{the}\:{velocity}\:{of}\:{ring}\:{then}. \\ $$$${Assume}\:{friction}\:{sufficient}\:{such} \\ $$$${that}\:{ring}\:{rolls}\:{purely}\:{as}\:{it}\:{moves}. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 14/Dec/18

$${pls}\:{mention}\:{the}\:{source}\:{of}\:{question}\:{and}\:{also} \\ $$$${attach}\:\:{the}\:{final}\:{answer}…{so}\:{that}\:{we}\:{can} \\ $$$${follow}\:{the}\:{right}\:{path}\:{to}\:{get}\:{the}\:{answer}… \\ $$$${because}\:{question}\:{it}\:{self}\:{is}\:{not}\:{clear}… \\ $$$$\left.\mathrm{1}\right)\:{if}\:{the}\:{thread}\:{gets}\:{unwinded}\:…{the}\:{ring}\:{has} \\ $$$${a}\:{tendency}\:{to}\:{rotate}\:{anticlockwise}… \\ $$$${further}\:{weight}\:{of}\:{block}\:{Mg}\:{cause}\:{the}\:{ring} \\ $$$${to}\:{get}\:{unwinded}… \\ $$$$ \\ $$

Commented by ajfour last updated on 14/Dec/18

$${which}\:{way}\:{do}\:{you}\:{think}\:{net}\:{torque}\: \\ $$$${on}\:{ring}\:{shall}\:{be},\:{Tanmay}\:{Sir}; \\ $$$${i}\:{seldom}\:{post}\:{questions}\:{from}\: \\ $$$${sources}. \\ $$

Commented by mr W last updated on 14/Dec/18

$${to}\:{me}\:{the}\:{question}\:{is}\:{clear}\:{and}\:{unique}.{the} \\ $$$${thread}\:{keeps}\:{in}\:{tension}. \\ $$

Answered by mr W last updated on 14/Dec/18

let θ=angle between string and ground length of string at t=0: a+(R/(tan (θ_0 /2)))=(h/(tan θ_0 ))=((h(1−tan^2 (θ_0 /2)))/(2tan (θ_0 /2))) δ_0 =tan (θ_0 /2) a+(R/δ_0 )=((h(1−δ_0 ^2 ))/(2δ_0 )) a=((h(1−δ_0 ^2 )−2R)/(2δ_0 )) δ_0 ^2 +2((a/h))δ_0 −(1−((2R)/h))=0 with α=(a/h) and γ=(R/h) δ_0 ^2 +2αδ_0 −(1−2γ)=0 ⇒δ_0 =(√(1+α^2 −2γ))−α=tan (θ_0 /2) l_0 =a+(h/(sin θ_0 ))−(R/(tan (θ_0 /2))) l_0 =a+((h−2R+hδ_0 ^2 )/(2δ_0 )) length of string at t=t_1 : R+(R/(tan (θ_1 /2)))=(h/(tan θ_1 ))=((h(1−tan^2 (θ_1 /2)))/(2tan (θ_1 /2))) R+(R/δ_1 )=((h(1−δ_1 ^2 ))/(2δ_1 )) R=((h(1−δ_1 ^2 )−2R)/(2δ_1 )) 2Rδ_1 =h−2R−hδ_1 ^2 δ_1 ^2 +2γδ_1 −(1−2γ)=0 ⇒δ_1 =(√(γ^2 +1−2γ))−γ=tan (θ_1 /2) l_1 =h−R+(h/(sin θ_1 ))−(R/(tan (θ_1 /2))) l_1 =h−R+((h−2R+hδ_1 ^2 )/(2δ_1 )) l_1 =l_0 +a−R h−R+((h−2R+hδ_1 ^2 )/(2δ_1 ))=a+((h−2R+hδ_0 ^2 )/(2δ_0 ))+a−R h+((h−2R+hδ_1 ^2 )/(2δ_1 ))=2a+((h−2R+hδ_0 ^2 )/(2δ_0 )) 1+((1−2γ+δ_1 ^2 )/(2δ_1 ))=2α+((1−2γ+δ_0 ^2 )/(2δ_0 )) ((1−2γ)/δ_1 )+δ_1 −((1−2γ)/δ_0 )−δ_0 =2(2α−1) ((1−2γ)/( (√(γ^2 +1−2γ))−γ))+(√(γ^2 +1−2γ))−γ−((1−2γ)/( (√(1+α^2 −2γ))−α))−(√(1+α^2 −2γ))+α=4α−2 ⇒3α+((1−2γ)/( (√(1+α^2 −2γ))−α))+(√(1+α^2 −2γ))=2−γ+((1−2γ)/( (√(γ^2 +1−2γ))−γ))+(√(γ^2 +1−2γ)) γ is constant, α is unknown ⇒solve for α=.... ⇒a=αh=..... at time t: position of block is y (above ground) position of ring is x x+(R/(tan (θ/2)))=(h/(tan θ))=((h(1−tan^2 (θ/2)))/(2tan (θ/2))) x+(R/δ)=((h(1−δ^2 ))/(2δ)) x=((h−2R−hδ^2 )/(2δ)) λ=(x/h)=((1−2γ−δ^2 )/(2δ)) δ^2 +2λδ−(1−2γ)=0 ⇒δ=(√(1+λ^2 −2γ))−λ (dδ/dt)=((λ/( (√(1+λ^2 −2γ))))−1)(1/h)×(dx/dt) l=h−y+(h/(sin θ))−(R/(tan (θ/2))) l=h−y+((h−2R+hδ^2 )/(2δ))=l_0 +a−x 1−(y/h)+((1−2γ+δ^2 )/(2δ))=2α+((1−2γ+δ_0 ^2 )/(2δ_0 ))−λ v_y =−(dy/dt)=velocity of block v=−(dx/dt)=velocity of ring (v_y /h)+[1−((1−2γ+δ^2 )/(2δ^2 ))](dδ/dt)=(v/h) (v_y /h)−(((δ^2 −1+2γ)/(2δ^2 )))((λ/( (√(1+λ^2 −2γ))))−1)(v/h)=(v/h) v_y ={1+(((δ^2 −1+2γ)/(2δ^2 )))((λ/( (√(1+λ^2 −2γ))))−1)}v at t=t_1 : δ=δ_1 , x=R, λ=(R/h)=γ v_y ={1+((((√(γ^2 +1−2γ))−γ)^2 −1+2γ)/(2((√(γ^2 +1−2γ))−γ)^2 ))((γ/( (√(1+γ^2 −2γ))))−1)}v ⇒v_y ={1+((γ(1−2γ))/((1−γ)((√(γ^2 +1−2γ))−γ)))}v (1/2)Mv^2 +(1/2)(MR^2 )ω^2 +(1/2)Mv_y ^2 =Mg(h−a−R) 2v^2 +v_y ^2 =2gh(1−α−γ) [2+{1+((γ(1−2γ))/((1−γ)((√(γ^2 +1−2γ))−γ)))}^2 ]v^2 =2gh(1−α−γ) ⇒v=(√((2gh(1−α−γ))/(2+{1+((γ(1−2γ))/((1−γ)((√(γ^2 +1−2γ))−γ)))}^2 )))

$${let}\:\theta={angle}\:{between}\:{string}\:{and}\:{ground} \\ $$$${length}\:{of}\:{string}\:{at}\:{t}=\mathrm{0}: \\ $$$${a}+\frac{{R}}{\mathrm{tan}\:\frac{\theta_{\mathrm{0}} }{\mathrm{2}}}=\frac{{h}}{\mathrm{tan}\:\theta_{\mathrm{0}} }=\frac{{h}\left(\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\frac{\theta_{\mathrm{0}} }{\mathrm{2}}\right)}{\mathrm{2tan}\:\frac{\theta_{\mathrm{0}} }{\mathrm{2}}} \\ $$$$\delta_{\mathrm{0}} =\mathrm{tan}\:\frac{\theta_{\mathrm{0}} }{\mathrm{2}} \\ $$$${a}+\frac{{R}}{\delta_{\mathrm{0}} }=\frac{{h}\left(\mathrm{1}−\delta_{\mathrm{0}} ^{\mathrm{2}} \right)}{\mathrm{2}\delta_{\mathrm{0}} } \\ $$$${a}=\frac{{h}\left(\mathrm{1}−\delta_{\mathrm{0}} ^{\mathrm{2}} \right)−\mathrm{2}{R}}{\mathrm{2}\delta_{\mathrm{0}} } \\ $$$$\delta_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2}\left(\frac{{a}}{{h}}\right)\delta_{\mathrm{0}} −\left(\mathrm{1}−\frac{\mathrm{2}{R}}{{h}}\right)=\mathrm{0} \\ $$$${with}\:\alpha=\frac{{a}}{{h}}\:{and}\:\gamma=\frac{{R}}{{h}} \\ $$$$\delta_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2}\alpha\delta_{\mathrm{0}} −\left(\mathrm{1}−\mathrm{2}\gamma\right)=\mathrm{0} \\ $$$$\Rightarrow\delta_{\mathrm{0}} =\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} −\mathrm{2}\gamma}−\alpha=\mathrm{tan}\:\frac{\theta_{\mathrm{0}} }{\mathrm{2}} \\ $$$${l}_{\mathrm{0}} ={a}+\frac{{h}}{\mathrm{sin}\:\theta_{\mathrm{0}} }−\frac{{R}}{\mathrm{tan}\:\frac{\theta_{\mathrm{0}} }{\mathrm{2}}} \\ $$$${l}_{\mathrm{0}} ={a}+\frac{{h}−\mathrm{2}{R}+{h}\delta_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{2}\delta_{\mathrm{0}} } \\ $$$${length}\:{of}\:{string}\:{at}\:{t}={t}_{\mathrm{1}} : \\ $$$${R}+\frac{{R}}{\mathrm{tan}\:\frac{\theta_{\mathrm{1}} }{\mathrm{2}}}=\frac{{h}}{\mathrm{tan}\:\theta_{\mathrm{1}} }=\frac{{h}\left(\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\frac{\theta_{\mathrm{1}} }{\mathrm{2}}\right)}{\mathrm{2tan}\:\frac{\theta_{\mathrm{1}} }{\mathrm{2}}} \\ $$$${R}+\frac{{R}}{\delta_{\mathrm{1}} }=\frac{{h}\left(\mathrm{1}−\delta_{\mathrm{1}} ^{\mathrm{2}} \right)}{\mathrm{2}\delta_{\mathrm{1}} } \\ $$$${R}=\frac{{h}\left(\mathrm{1}−\delta_{\mathrm{1}} ^{\mathrm{2}} \right)−\mathrm{2}{R}}{\mathrm{2}\delta_{\mathrm{1}} } \\ $$$$\mathrm{2}{R}\delta_{\mathrm{1}} ={h}−\mathrm{2}{R}−{h}\delta_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\delta_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{2}\gamma\delta_{\mathrm{1}} −\left(\mathrm{1}−\mathrm{2}\gamma\right)=\mathrm{0} \\ $$$$\Rightarrow\delta_{\mathrm{1}} =\sqrt{\gamma^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\gamma}−\gamma=\mathrm{tan}\:\frac{\theta_{\mathrm{1}} }{\mathrm{2}} \\ $$$${l}_{\mathrm{1}} ={h}−{R}+\frac{{h}}{\mathrm{sin}\:\theta_{\mathrm{1}} }−\frac{{R}}{\mathrm{tan}\:\frac{\theta_{\mathrm{1}} }{\mathrm{2}}} \\ $$$${l}_{\mathrm{1}} ={h}−{R}+\frac{{h}−\mathrm{2}{R}+{h}\delta_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}\delta_{\mathrm{1}} } \\ $$$${l}_{\mathrm{1}} ={l}_{\mathrm{0}} +{a}−{R} \\ $$$${h}−{R}+\frac{{h}−\mathrm{2}{R}+{h}\delta_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}\delta_{\mathrm{1}} }={a}+\frac{{h}−\mathrm{2}{R}+{h}\delta_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{2}\delta_{\mathrm{0}} }+{a}−{R} \\ $$$${h}+\frac{{h}−\mathrm{2}{R}+{h}\delta_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}\delta_{\mathrm{1}} }=\mathrm{2}{a}+\frac{{h}−\mathrm{2}{R}+{h}\delta_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{2}\delta_{\mathrm{0}} } \\ $$$$\mathrm{1}+\frac{\mathrm{1}−\mathrm{2}\gamma+\delta_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}\delta_{\mathrm{1}} }=\mathrm{2}\alpha+\frac{\mathrm{1}−\mathrm{2}\gamma+\delta_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{2}\delta_{\mathrm{0}} } \\ $$$$\frac{\mathrm{1}−\mathrm{2}\gamma}{\delta_{\mathrm{1}} }+\delta_{\mathrm{1}} −\frac{\mathrm{1}−\mathrm{2}\gamma}{\delta_{\mathrm{0}} }−\delta_{\mathrm{0}} =\mathrm{2}\left(\mathrm{2}\alpha−\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}−\mathrm{2}\gamma}{\:\sqrt{\gamma^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\gamma}−\gamma}+\sqrt{\gamma^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\gamma}−\gamma−\frac{\mathrm{1}−\mathrm{2}\gamma}{\:\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} −\mathrm{2}\gamma}−\alpha}−\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} −\mathrm{2}\gamma}+\alpha=\mathrm{4}\alpha−\mathrm{2} \\ $$$$\Rightarrow\mathrm{3}\alpha+\frac{\mathrm{1}−\mathrm{2}\gamma}{\:\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} −\mathrm{2}\gamma}−\alpha}+\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} −\mathrm{2}\gamma}=\mathrm{2}−\gamma+\frac{\mathrm{1}−\mathrm{2}\gamma}{\:\sqrt{\gamma^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\gamma}−\gamma}+\sqrt{\gamma^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\gamma} \\ $$$$\gamma\:{is}\:{constant},\:\alpha\:{is}\:{unknown} \\ $$$$\Rightarrow{solve}\:{for}\:\alpha=…. \\ $$$$\Rightarrow{a}=\alpha{h}=….. \\ $$$$ \\ $$$${at}\:{time}\:{t}: \\ $$$${position}\:{of}\:{block}\:{is}\:{y}\:\left({above}\:{ground}\right) \\ $$$${position}\:{of}\:{ring}\:{is}\:{x} \\ $$$${x}+\frac{{R}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}=\frac{{h}}{\mathrm{tan}\:\theta}=\frac{{h}\left(\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}\right)}{\mathrm{2tan}\:\frac{\theta}{\mathrm{2}}} \\ $$$${x}+\frac{{R}}{\delta}=\frac{{h}\left(\mathrm{1}−\delta^{\mathrm{2}} \right)}{\mathrm{2}\delta} \\ $$$${x}=\frac{{h}−\mathrm{2}{R}−{h}\delta^{\mathrm{2}} }{\mathrm{2}\delta} \\ $$$$\lambda=\frac{{x}}{{h}}=\frac{\mathrm{1}−\mathrm{2}\gamma−\delta^{\mathrm{2}} }{\mathrm{2}\delta} \\ $$$$\delta^{\mathrm{2}} +\mathrm{2}\lambda\delta−\left(\mathrm{1}−\mathrm{2}\gamma\right)=\mathrm{0} \\ $$$$\Rightarrow\delta=\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} −\mathrm{2}\gamma}−\lambda \\ $$$$\frac{{d}\delta}{{dt}}=\left(\frac{\lambda}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} −\mathrm{2}\gamma}}−\mathrm{1}\right)\frac{\mathrm{1}}{{h}}×\frac{{dx}}{{dt}} \\ $$$${l}={h}−{y}+\frac{{h}}{\mathrm{sin}\:\theta}−\frac{{R}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}} \\ $$$${l}={h}−{y}+\frac{{h}−\mathrm{2}{R}+{h}\delta^{\mathrm{2}} }{\mathrm{2}\delta}={l}_{\mathrm{0}} +{a}−{x} \\ $$$$\mathrm{1}−\frac{{y}}{{h}}+\frac{\mathrm{1}−\mathrm{2}\gamma+\delta^{\mathrm{2}} }{\mathrm{2}\delta}=\mathrm{2}\alpha+\frac{\mathrm{1}−\mathrm{2}\gamma+\delta_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{2}\delta_{\mathrm{0}} }−\lambda \\ $$$${v}_{{y}} =−\frac{{dy}}{{dt}}={velocity}\:{of}\:{block} \\ $$$${v}=−\frac{{dx}}{{dt}}={velocity}\:{of}\:{ring} \\ $$$$\frac{{v}_{{y}} }{{h}}+\left[\mathrm{1}−\frac{\mathrm{1}−\mathrm{2}\gamma+\delta^{\mathrm{2}} }{\mathrm{2}\delta^{\mathrm{2}} }\right]\frac{{d}\delta}{{dt}}=\frac{{v}}{{h}} \\ $$$$\frac{{v}_{{y}} }{{h}}−\left(\frac{\delta^{\mathrm{2}} −\mathrm{1}+\mathrm{2}\gamma}{\mathrm{2}\delta^{\mathrm{2}} }\right)\left(\frac{\lambda}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} −\mathrm{2}\gamma}}−\mathrm{1}\right)\frac{{v}}{{h}}=\frac{{v}}{{h}} \\ $$$${v}_{{y}} =\left\{\mathrm{1}+\left(\frac{\delta^{\mathrm{2}} −\mathrm{1}+\mathrm{2}\gamma}{\mathrm{2}\delta^{\mathrm{2}} }\right)\left(\frac{\lambda}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} −\mathrm{2}\gamma}}−\mathrm{1}\right)\right\}{v} \\ $$$${at}\:{t}={t}_{\mathrm{1}} :\:\delta=\delta_{\mathrm{1}} ,\:{x}={R},\:\lambda=\frac{{R}}{{h}}=\gamma \\ $$$${v}_{{y}} =\left\{\mathrm{1}+\frac{\left(\sqrt{\gamma^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\gamma}−\gamma\right)^{\mathrm{2}} −\mathrm{1}+\mathrm{2}\gamma}{\mathrm{2}\left(\sqrt{\gamma^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\gamma}−\gamma\right)^{\mathrm{2}} }\left(\frac{\gamma}{\:\sqrt{\mathrm{1}+\gamma^{\mathrm{2}} −\mathrm{2}\gamma}}−\mathrm{1}\right)\right\}{v} \\ $$$$\Rightarrow{v}_{{y}} =\left\{\mathrm{1}+\frac{\gamma\left(\mathrm{1}−\mathrm{2}\gamma\right)}{\left(\mathrm{1}−\gamma\right)\left(\sqrt{\gamma^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\gamma}−\gamma\right)}\right\}{v} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{Mv}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\left({MR}^{\mathrm{2}} \right)\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{Mv}_{{y}} ^{\mathrm{2}} ={Mg}\left({h}−{a}−{R}\right) \\ $$$$\mathrm{2}{v}^{\mathrm{2}} +{v}_{{y}} ^{\mathrm{2}} =\mathrm{2}{gh}\left(\mathrm{1}−\alpha−\gamma\right) \\ $$$$\left[\mathrm{2}+\left\{\mathrm{1}+\frac{\gamma\left(\mathrm{1}−\mathrm{2}\gamma\right)}{\left(\mathrm{1}−\gamma\right)\left(\sqrt{\gamma^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\gamma}−\gamma\right)}\right\}^{\mathrm{2}} \right]{v}^{\mathrm{2}} =\mathrm{2}{gh}\left(\mathrm{1}−\alpha−\gamma\right) \\ $$$$\Rightarrow{v}=\sqrt{\frac{\mathrm{2}{gh}\left(\mathrm{1}−\alpha−\gamma\right)}{\mathrm{2}+\left\{\mathrm{1}+\frac{\gamma\left(\mathrm{1}−\mathrm{2}\gamma\right)}{\left(\mathrm{1}−\gamma\right)\left(\sqrt{\gamma^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\gamma}−\gamma\right)}\right\}^{\mathrm{2}} }} \\ $$

Commented by ajfour last updated on 14/Dec/18

$${Plentiful}\:{of}\:{mind}\:{and}\:{effort}\:{Sir}; \\ $$$${thanks},\:{let}\:{me}\:{time}\:{to}\:{follow}\:{it} \\ $$$${entirely}.. \\ $$

Commented by mr W last updated on 14/Dec/18

Commented by mr W last updated on 14/Dec/18

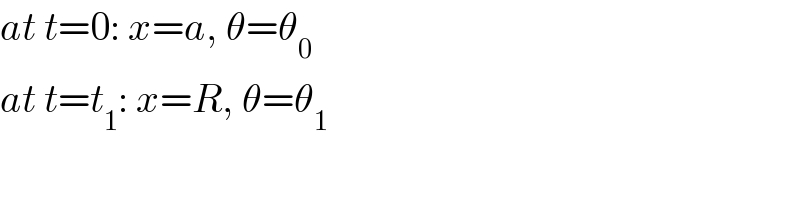
at t=0: x=a, θ=θ_0 at t=t_1 : x=R, θ=θ_1

$${at}\:{t}=\mathrm{0}:\:{x}={a},\:\theta=\theta_{\mathrm{0}} \\ $$$${at}\:{t}={t}_{\mathrm{1}} :\:{x}={R},\:\theta=\theta_{\mathrm{1}} \\ $$

Commented by ajfour last updated on 16/Dec/18

$${Very}\:{brilliant}\:{Sir},\:\mathcal{AWESOME}\:! \\ $$

Answered by ajfour last updated on 14/Dec/18

Commented by ajfour last updated on 14/Dec/18

let initially θ = α, x=a, y=a, z= l finally θ=β, x=R, y=h−R, z= s x+Rcos θ = zsin θ R+Rsin θ = h−zcos θ ⇒ R+Rsin θ = h−z(((zsin θ−x)/R)) ⇒ sin θ = ((h−R+((xz)/R))/(R+(z^2 /R))) ________________________ ⇒ sin α = ((h−R+((al)/R))/(R+(l^2 /R))) ...(i) & sin β = ((h−R+s)/(R+(s^2 /R))) ...(ii) l^2 = (h−R−Rsin α)^2 +a^2 ...(iii) s^2 = (h−R−Rsin β)^2 +R^2 ....(iv) from length of string , (αR+l+a) − (βR+s+R)= a−R ...(v) unknowns are : α, β, l, s, a

$${let}\:{initially}\:\:\theta\:=\:\alpha,\:\:{x}={a},\:\:{y}={a},\:\:{z}=\:{l} \\ $$$${finally}\:\:\:\:\:\theta=\beta,\:\:{x}={R},\:\:{y}={h}−{R},\:{z}=\:{s} \\ $$$${x}+{R}\mathrm{cos}\:\theta\:=\:{z}\mathrm{sin}\:\theta \\ $$$${R}+{R}\mathrm{sin}\:\theta\:=\:{h}−{z}\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\:{R}+{R}\mathrm{sin}\:\theta\:=\:{h}−{z}\left(\frac{{z}\mathrm{sin}\:\theta−{x}}{{R}}\right) \\ $$$$\Rightarrow\:\:\:\mathrm{sin}\:\theta\:=\:\frac{{h}−{R}+\frac{{xz}}{{R}}}{{R}+\frac{{z}^{\mathrm{2}} }{{R}}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:\:\:\mathrm{sin}\:\alpha\:=\:\frac{{h}−{R}+\frac{{al}}{{R}}}{{R}+\frac{{l}^{\mathrm{2}} }{{R}}}\:\:\:\:\:\:\:\:\:\:…\left({i}\right) \\ $$$$\&\:\:\:\:\:\mathrm{sin}\:\beta\:=\:\frac{{h}−{R}+{s}}{{R}+\frac{{s}^{\mathrm{2}} }{{R}}}\:\:\:\:\:\:\:\:\:\:\:\:\:…\left({ii}\right) \\ $$$$\:\:{l}^{\mathrm{2}} \:=\:\left({h}−{R}−{R}\mathrm{sin}\:\alpha\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \:\:\:\:\:\:\:\:…\left({iii}\right) \\ $$$$\:\:{s}^{\mathrm{2}} \:=\:\left({h}−{R}−{R}\mathrm{sin}\:\beta\right)^{\mathrm{2}} +{R}^{\mathrm{2}} \:\:\:\:\:\:….\left({iv}\right) \\ $$$${from}\:{length}\:{of}\:{string}\:, \\ $$$$\:\:\:\left(\alpha{R}+{l}+{a}\right)\:−\:\left(\beta{R}+{s}+{R}\right)=\:{a}−{R} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\left({v}\right) \\ $$$${unknowns}\:{are}\::\:\alpha,\:\beta,\:{l},\:{s},\:\boldsymbol{{a}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply