Question Number 50135 by peter frank last updated on 14/Dec/18

Commented by maxmathsup by imad last updated on 01/Jan/19
![let solve (2x−1)y^(′′) −y^′ =0 withy(0)=2 and y^′ (0)=3 let use changement y^′ =Z ⇒(2x−1)z^′ −z =0 ⇒(2x−1)z^′ =z ⇒(z^′ /z) =(1/(2x−1)) ⇒ln∣z∣=(1/2)ln∣2x−1∣+k ⇒ ⇒z =K(√(∣2x−1∣)) let take x<(1/2) ⇒z =K(√(−2x+1)) ⇒y^′ =k (√(−2x+1)) ⇒ y =k ∫ (√(−2x+1))dx +c_0 =k ∫ (−2x+1)^(1/2) dx +c_0 =k (2/3)(−(1/2))(−2x+1)^(3/2) +c_0 =c_0 −(k/3)(−2x+1)^(3/2) ⇒ y(x) =c_0 −(k/3)(−2x+1)(√(−2x+1)) y(0)=2 ⇒c_0 −(k/3) =2 ⇒3c_0 −k =6 y^′ (0)=3 ⇒z(0)=3 ⇒k=3 ⇒3c_0 =9 ⇒c_0 =3 ⇒y(x)=3−(−2x+1)(√(−2x+1)) ⇒y(x)=3+(2x−1)(√(−2x+1)) this is the solution on]−∞,(1/2)[. z](https://www.tinkutara.com/question/Q51945.png)
$${let}\:{solve}\:\left(\mathrm{2}{x}−\mathrm{1}\right){y}^{''} \:−{y}^{'} =\mathrm{0}\:\:\:{withy}\left(\mathrm{0}\right)=\mathrm{2}\:{and}\:{y}^{'} \left(\mathrm{0}\right)=\mathrm{3}\:\:{let}\:{use}\:{changement} \\ $$$${y}^{'} \:={Z}\:\Rightarrow\left(\mathrm{2}{x}−\mathrm{1}\right){z}^{'} −{z}\:=\mathrm{0}\:\Rightarrow\left(\mathrm{2}{x}−\mathrm{1}\right){z}^{'} ={z}\:\Rightarrow\frac{{z}^{'} }{{z}}\:=\frac{\mathrm{1}}{\mathrm{2}{x}−\mathrm{1}}\:\Rightarrow{ln}\mid{z}\mid=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{2}{x}−\mathrm{1}\mid+{k}\:\Rightarrow \\ $$$$\Rightarrow{z}\:={K}\sqrt{\mid\mathrm{2}{x}−\mathrm{1}\mid}\:\:{let}\:{take}\:\:{x}<\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{z}\:={K}\sqrt{−\mathrm{2}{x}+\mathrm{1}}\:\:\Rightarrow{y}^{'} ={k}\:\sqrt{−\mathrm{2}{x}+\mathrm{1}}\:\Rightarrow \\ $$$${y}\:={k}\:\int\:\:\:\sqrt{−\mathrm{2}{x}+\mathrm{1}}{dx}\:\:+{c}_{\mathrm{0}} \:={k}\:\int\:\:\:\left(−\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dx}\:+{c}_{\mathrm{0}} \\ $$$$={k}\:\frac{\mathrm{2}}{\mathrm{3}}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:+{c}_{\mathrm{0}} ={c}_{\mathrm{0}} −\frac{{k}}{\mathrm{3}}\left(−\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\Rightarrow \\ $$$${y}\left({x}\right)\:={c}_{\mathrm{0}} −\frac{{k}}{\mathrm{3}}\left(−\mathrm{2}{x}+\mathrm{1}\right)\sqrt{−\mathrm{2}{x}+\mathrm{1}} \\ $$$${y}\left(\mathrm{0}\right)=\mathrm{2}\:\Rightarrow{c}_{\mathrm{0}} −\frac{{k}}{\mathrm{3}}\:=\mathrm{2}\:\Rightarrow\mathrm{3}{c}_{\mathrm{0}} −{k}\:=\mathrm{6} \\ $$$${y}^{'} \left(\mathrm{0}\right)=\mathrm{3}\:\Rightarrow{z}\left(\mathrm{0}\right)=\mathrm{3}\:\Rightarrow{k}=\mathrm{3}\:\Rightarrow\mathrm{3}{c}_{\mathrm{0}} =\mathrm{9}\:\Rightarrow{c}_{\mathrm{0}} =\mathrm{3}\:\Rightarrow{y}\left({x}\right)=\mathrm{3}−\left(−\mathrm{2}{x}+\mathrm{1}\right)\sqrt{−\mathrm{2}{x}+\mathrm{1}} \\ $$$$\left.\Rightarrow{y}\left({x}\right)=\mathrm{3}+\left(\mathrm{2}{x}−\mathrm{1}\right)\sqrt{−\mathrm{2}{x}+\mathrm{1}}\:\:\:{this}\:{is}\:{the}\:{solution}\:{on}\right]−\infty,\frac{\mathrm{1}}{\mathrm{2}}\left[.\right. \\ $$$${z} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 01/Jan/19
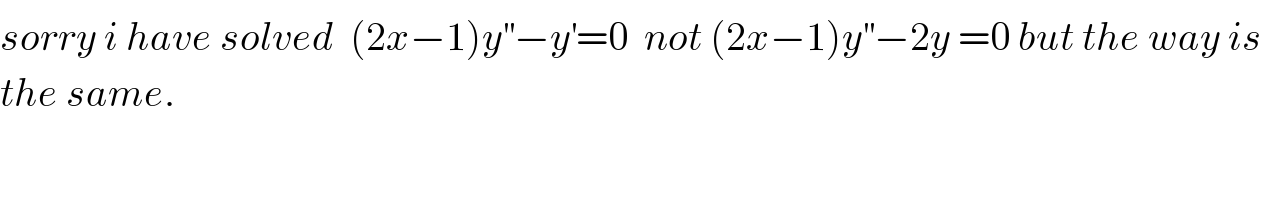
$${sorry}\:{i}\:{have}\:{solved}\:\:\left(\mathrm{2}{x}−\mathrm{1}\right){y}^{''} −{y}^{'} =\mathrm{0}\:\:{not}\:\left(\mathrm{2}{x}−\mathrm{1}\right){y}^{''} −\mathrm{2}{y}\:=\mathrm{0}\:{but}\:{the}\:{way}\:{is} \\ $$$${the}\:{same}. \\ $$
Answered by peter frank last updated on 14/Dec/18
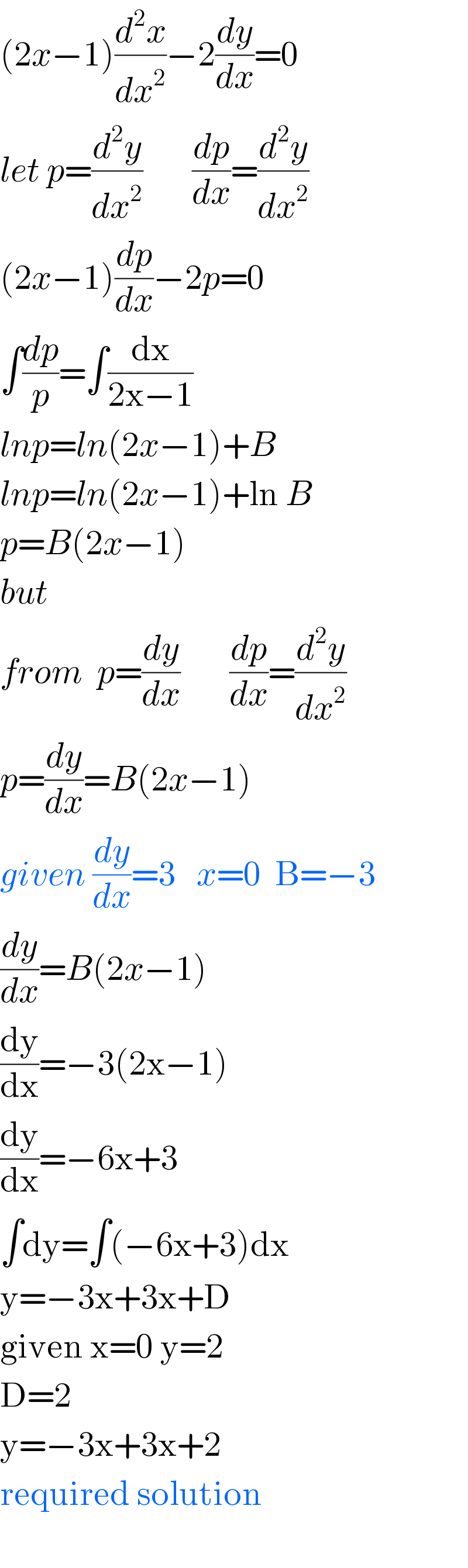
$$\left(\mathrm{2}{x}−\mathrm{1}\right)\frac{{d}^{\mathrm{2}} {x}}{{dx}^{\mathrm{2}} }−\mathrm{2}\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$${let}\:{p}=\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:\:\:\:\:\:\:\frac{{dp}}{{dx}}=\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} } \\ $$$$\left(\mathrm{2}{x}−\mathrm{1}\right)\frac{{dp}}{{dx}}−\mathrm{2}{p}=\mathrm{0} \\ $$$$\int\frac{{dp}}{{p}}=\int\frac{\mathrm{dx}}{\mathrm{2x}−\mathrm{1}} \\ $$$${lnp}={ln}\left(\mathrm{2}{x}−\mathrm{1}\right)+{B} \\ $$$${lnp}={ln}\left(\mathrm{2}{x}−\mathrm{1}\right)+\mathrm{ln}\:{B} \\ $$$${p}={B}\left(\mathrm{2}{x}−\mathrm{1}\right) \\ $$$${but} \\ $$$${from}\:\:{p}=\frac{{dy}}{{dx}}\:\:\:\:\:\:\:\frac{{dp}}{{dx}}=\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} } \\ $$$${p}=\frac{{dy}}{{dx}}={B}\left(\mathrm{2}{x}−\mathrm{1}\right) \\ $$$${given}\:\frac{{dy}}{{dx}}=\mathrm{3}\:\:\:{x}=\mathrm{0}\:\:\mathrm{B}=−\mathrm{3} \\ $$$$\frac{{dy}}{{dx}}={B}\left(\mathrm{2}{x}−\mathrm{1}\right) \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=−\mathrm{3}\left(\mathrm{2x}−\mathrm{1}\right) \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=−\mathrm{6x}+\mathrm{3} \\ $$$$\int\mathrm{dy}=\int\left(−\mathrm{6x}+\mathrm{3}\right)\mathrm{dx} \\ $$$$\mathrm{y}=−\mathrm{3x}+\mathrm{3x}+\mathrm{D} \\ $$$$\mathrm{given}\:\mathrm{x}=\mathrm{0}\:\mathrm{y}=\mathrm{2} \\ $$$$\mathrm{D}=\mathrm{2} \\ $$$$\mathrm{y}=−\mathrm{3x}+\mathrm{3x}+\mathrm{2} \\ $$$$\mathrm{required}\:\mathrm{solution} \\ $$$$ \\ $$
Answered by peter frank last updated on 14/Dec/18
![x(x+y)(dy/dx)=x^2 +xy−3y^2 (1+(y/x))(dy/dx)=1+(y/x)−3((y/(x )))^2 from y=vx (dy/dx)=v+x(dy/dx) (1+v)(v+x(dy/dx))=1+v−3v^2 (((1+v))/(1−4v^2 ))dv=(dx/x) ∫((vdv)/(1−4v^2 ))+∫(dv/(1−4v^2 ))=ln x+A −(1/8)∫((8v)/(1−4v^2 ))dv+(1/2)∫(dv/(1−2v))+(1/2)∫(dv/(1−2v))=lnx+A −ln (1−4v^2 )−2ln (1−2v)+2ln (1+2v)=8ln (Ax) ln[(((1+2v)^2 )/((1−2v)^2 (1−4v^2 )))]=ln A^8 x^8 ((1+2v)/(1−2v)^3 ))=A^8 x^8 A^8 =C but v=(y/x) and simplify x+2y=Cx^6 (x−2y)^3 Required solution](https://www.tinkutara.com/question/Q50144.png)
$$\mathrm{x}\left(\mathrm{x}+\mathrm{y}\right)\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{x}^{\mathrm{2}} +\mathrm{xy}−\mathrm{3y}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{y}}{\mathrm{x}}\right)\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{1}+\frac{\mathrm{y}}{\mathrm{x}}−\mathrm{3}\left(\frac{\mathrm{y}}{\mathrm{x}\:}\right)^{\mathrm{2}} \\ $$$$\mathrm{from}\:\mathrm{y}=\mathrm{vx} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{v}+\mathrm{x}\frac{\mathrm{dy}}{\mathrm{dx}} \\ $$$$\left(\mathrm{1}+\mathrm{v}\right)\left(\mathrm{v}+\mathrm{x}\frac{\mathrm{dy}}{\mathrm{dx}}\right)=\mathrm{1}+\mathrm{v}−\mathrm{3v}^{\mathrm{2}} \\ $$$$\frac{\left(\mathrm{1}+\mathrm{v}\right)}{\mathrm{1}−\mathrm{4v}^{\mathrm{2}} }\mathrm{dv}=\frac{\mathrm{dx}}{\mathrm{x}} \\ $$$$\int\frac{\mathrm{vdv}}{\mathrm{1}−\mathrm{4v}^{\mathrm{2}} }+\int\frac{\mathrm{dv}}{\mathrm{1}−\mathrm{4v}^{\mathrm{2}} }=\mathrm{ln}\:\mathrm{x}+\mathrm{A} \\ $$$$−\frac{\mathrm{1}}{\mathrm{8}}\int\frac{\mathrm{8v}}{\mathrm{1}−\mathrm{4v}^{\mathrm{2}} }\mathrm{dv}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dv}}{\mathrm{1}−\mathrm{2v}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dv}}{\mathrm{1}−\mathrm{2v}}=\mathrm{lnx}+\mathrm{A} \\ $$$$−\mathrm{ln}\:\left(\mathrm{1}−\mathrm{4v}^{\mathrm{2}} \right)−\mathrm{2ln}\:\left(\mathrm{1}−\mathrm{2v}\right)+\mathrm{2ln}\:\left(\mathrm{1}+\mathrm{2v}\right)=\mathrm{8ln}\:\left(\mathrm{Ax}\right) \\ $$$$\mathrm{ln}\left[\frac{\left(\mathrm{1}+\mathrm{2v}\right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{2v}\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{4v}^{\mathrm{2}} \right)}\right]=\mathrm{ln}\:\mathrm{A}^{\mathrm{8}} \mathrm{x}^{\mathrm{8}} \\ $$$$\frac{\mathrm{1}+\mathrm{2v}}{\left.\mathrm{1}−\mathrm{2v}\right)^{\mathrm{3}} }=\mathrm{A}^{\mathrm{8}} \mathrm{x}^{\mathrm{8}} \:\:\:\:\:\mathrm{A}^{\mathrm{8}} =\mathrm{C} \\ $$$$\mathrm{but}\:\:\mathrm{v}=\frac{\mathrm{y}}{\mathrm{x}}\:\mathrm{and}\:\mathrm{simplify} \\ $$$$\mathrm{x}+\mathrm{2y}=\mathrm{Cx}^{\mathrm{6}} \left(\mathrm{x}−\mathrm{2y}\right)^{\mathrm{3}} \\ $$$$\mathrm{Required}\:\mathrm{solution} \\ $$$$ \\ $$
