Menu Close

Question-50219

Tinku Tara 0 Comments
Pin




Question Number 50219 by cesar.marval.larez@gmail.com last updated on 14/Dec/18
Answered by peter frank last updated on 15/Dec/18
all question above lie on the concept(partial fraction) ∫((5x+3)/(x^3 −2x^2 −2x))=∫((5x+3)/(x(x+1)(x−3))) (A/(x ))+(B/(x−3 ))+(C/(x+1)) A=−1 B=(3/2) C=−(1/2) ∫−(1/(x ))dx+(3/2)∫(dx/(x−3 ))+−(1/2)∫(dx/(x+1)) −ln x+(3/2)ln (x−3)−(1/2)ln (x+1)+M
$${all}\:{question}\:{above}\:\:{lie}\:{on}\:{the}\:{concept}\left({partial}\:{fraction}\right) \\ $$$$\int\frac{\mathrm{5x}+\mathrm{3}}{\mathrm{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2x}}=\int\frac{\mathrm{5x}+\mathrm{3}}{{x}\left({x}+\mathrm{1}\right)\left({x}−\mathrm{3}\right)} \\ $$$$\frac{\mathrm{A}}{\mathrm{x}\:}+\frac{\mathrm{B}}{\mathrm{x}−\mathrm{3}\:}+\frac{\mathrm{C}}{\mathrm{x}+\mathrm{1}} \\ $$$$\mathrm{A}=−\mathrm{1}\:\:\mathrm{B}=\frac{\mathrm{3}}{\mathrm{2}}\:\:\:\mathrm{C}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\int−\frac{\mathrm{1}}{\mathrm{x}\:}\mathrm{dx}+\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{dx}}{\mathrm{x}−\mathrm{3}\:}+−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dx}}{\mathrm{x}+\mathrm{1}} \\ $$$$−\mathrm{ln}\:\mathrm{x}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\:\left({x}−\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({x}+\mathrm{1}\right)+{M} \\ $$$$ \\ $$
Answered by afachri last updated on 15/Dec/18
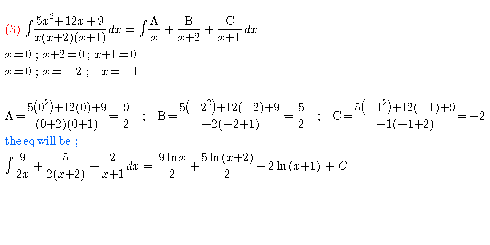
Answered by afachri last updated on 15/Dec/18
Commented by Abdo msup. last updated on 23/Dec/18
let decompose F(x)= ((3x^2 −21x +32)/(x(x−4)^2 )) F(x)= (a/x) +(b/(x−4)) +(c/((x−4)^2 )) c =lim_(x→4) (x−4)^2 F(x)=((3.16−21.4 +32)/4) =12−21 +8 =−1 ⇒F(x)=(a/x) +(b/(x−4)) −(1/((x−4)^2 )) lim_(x→+∞) xF(x)=3 =a+b F(1) = ((3−21+32)/9) =((35−21)/9) =((14)/9) =a−(b/3) −(1/9) ⇒ 14 =9a−3b−1 ⇒9a−3b=15 ⇒3a−b =5 ⇒ 3a−(3−a)=5 ⇒4a=8 ⇒a=2 and b=1 ⇒ F(x)=(2/x) +(1/(x−4)) −(1/((x−4)^2 )) ⇒ ∫ F(x)dx =2ln∣x∣+ln∣x−4∣+(1/(x−4)) +c .
$${let}\:{decompose}\:{F}\left({x}\right)=\:\frac{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{21}{x}\:+\mathrm{32}}{{x}\left({x}−\mathrm{4}\right)^{\mathrm{2}} } \\ $$$${F}\left({x}\right)=\:\frac{{a}}{{x}}\:+\frac{{b}}{{x}−\mathrm{4}}\:+\frac{{c}}{\left({x}−\mathrm{4}\right)^{\mathrm{2}} } \\ $$$${c}\:={lim}_{{x}\rightarrow\mathrm{4}} \left({x}−\mathrm{4}\right)^{\mathrm{2}} {F}\left({x}\right)=\frac{\mathrm{3}.\mathrm{16}−\mathrm{21}.\mathrm{4}\:+\mathrm{32}}{\mathrm{4}} \\ $$$$=\mathrm{12}−\mathrm{21}\:+\mathrm{8}\:=−\mathrm{1}\:\Rightarrow{F}\left({x}\right)=\frac{{a}}{{x}}\:+\frac{{b}}{{x}−\mathrm{4}}\:−\frac{\mathrm{1}}{\left({x}−\mathrm{4}\right)^{\mathrm{2}} } \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)=\mathrm{3}\:={a}+{b} \\ $$$${F}\left(\mathrm{1}\right)\:=\:\frac{\mathrm{3}−\mathrm{21}+\mathrm{32}}{\mathrm{9}}\:=\frac{\mathrm{35}−\mathrm{21}}{\mathrm{9}}\:=\frac{\mathrm{14}}{\mathrm{9}}\:={a}−\frac{{b}}{\mathrm{3}}\:−\frac{\mathrm{1}}{\mathrm{9}}\:\Rightarrow \\ $$$$\mathrm{14}\:=\mathrm{9}{a}−\mathrm{3}{b}−\mathrm{1}\:\Rightarrow\mathrm{9}{a}−\mathrm{3}{b}=\mathrm{15}\:\Rightarrow\mathrm{3}{a}−{b}\:=\mathrm{5}\:\Rightarrow \\ $$$$\mathrm{3}{a}−\left(\mathrm{3}−{a}\right)=\mathrm{5}\:\Rightarrow\mathrm{4}{a}=\mathrm{8}\:\Rightarrow{a}=\mathrm{2}\:\:{and}\:{b}=\mathrm{1}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{\mathrm{2}}{{x}}\:+\frac{\mathrm{1}}{{x}−\mathrm{4}}\:−\frac{\mathrm{1}}{\left({x}−\mathrm{4}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int\:{F}\left({x}\right){dx}\:=\mathrm{2}{ln}\mid{x}\mid+{ln}\mid{x}−\mathrm{4}\mid+\frac{\mathrm{1}}{{x}−\mathrm{4}}\:+{c}\:. \\ $$
Commented by Abdo msup. last updated on 23/Dec/18
i see that the decomposition in given answer is not correct but the result is correct.
$${i}\:{see}\:{that}\:{the}\:{decomposition}\:{in}\:{given}\:{answer}\:{is} \\ $$$${not}\:{correct}\:{but}\:{the}\:{result}\:{is}\:{correct}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Dec/18
3)∫((5x^2 +12x+9)/(x(x^2 +3x+2)))dx ∫((5x^2 +12x+9)/(x(x+1)(x+2)))dx=∫(a/x)+(b/(x+1))+(c/(x+2))dx alnx+bln(x+1)+cln(x+2)+d now calculating a,b,c 5x^2 +12x+9=a(x+1)(x+2)+bx(x+2)+cx(x+1) put x=0 9=2a a=(9/2) put x+1=0 5(−1)^2 +12(−1)+9=b×−1×(−1+2) 2=−b b=−2 put x+2=0 5(−2)^2 +12(−2)+9=c×−2×(−2+1) 5=2c c=(5/2) so abswer is (9/2)lnx−2ln(x+1)+(5/2)ln(x+2)+d
$$\left.\mathrm{3}\right)\int\frac{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{12}{x}+\mathrm{9}}{{x}\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{2}\right)}{dx} \\ $$$$\int\frac{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{12}{x}+\mathrm{9}}{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)}{dx}=\int\frac{{a}}{{x}}+\frac{{b}}{{x}+\mathrm{1}}+\frac{{c}}{{x}+\mathrm{2}}{dx} \\ $$$${alnx}+{bln}\left({x}+\mathrm{1}\right)+{cln}\left({x}+\mathrm{2}\right)+{d} \\ $$$${now}\:{calculating}\:{a},{b},{c} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} +\mathrm{12}{x}+\mathrm{9}={a}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)+{bx}\left({x}+\mathrm{2}\right)+{cx}\left({x}+\mathrm{1}\right) \\ $$$${put}\:{x}=\mathrm{0} \\ $$$$\mathrm{9}=\mathrm{2}{a}\:\:\:{a}=\frac{\mathrm{9}}{\mathrm{2}} \\ $$$${put}\:{x}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{5}\left(−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{12}\left(−\mathrm{1}\right)+\mathrm{9}={b}×−\mathrm{1}×\left(−\mathrm{1}+\mathrm{2}\right) \\ $$$$\mathrm{2}=−{b}\:\:\:{b}=−\mathrm{2} \\ $$$${put}\:{x}+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{5}\left(−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{12}\left(−\mathrm{2}\right)+\mathrm{9}={c}×−\mathrm{2}×\left(−\mathrm{2}+\mathrm{1}\right) \\ $$$$\mathrm{5}=\mathrm{2}{c}\:\:{c}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$${so}\:{abswer}\:{is} \\ $$$$\frac{\mathrm{9}}{\mathrm{2}}{lnx}−\mathrm{2}{ln}\left({x}+\mathrm{1}\right)+\frac{\mathrm{5}}{\mathrm{2}}{ln}\left({x}+\mathrm{2}\right)+{d} \\ $$
Commented by cesar.marval.larez@gmail.com last updated on 15/Dec/18
my problem is the beginning to descompose, thank u my friend
$${my}\:{problem}\:{is}\:{the}\:{beginning}\:{to} \\ $$$${descompose},\:{thank}\:{u}\:{my}\:{friend} \\ $$
Answered by afachri last updated on 15/Dec/18
Commented by Abdo msup. last updated on 23/Dec/18
let decompose F(x)=((2x^2 +x−4)/(x(x−2)(x+1))) F(x)=(a/x) +(b/(x−2)) +(c/(x+1)) a =lim_(x→0) xF(x)=((−4)/((−2))) =2 b =lim_(x→2) (x−2)F(x)=(6/6) =1 c =lim_(x→−1) (x+1)F(x)= ((−3)/3)=−1 ⇒ F(x) =(2/x) +(1/(x−2)) −(1/((x+1)))⇒ ∫ F(x)dx?=2ln∣x∣+ln∣x−2∣−ln∣x+1∣ +c .
$${let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{2}{x}^{\mathrm{2}} \:+{x}−\mathrm{4}}{{x}\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)} \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}}\:+\frac{{b}}{{x}−\mathrm{2}}\:+\frac{{c}}{{x}+\mathrm{1}} \\ $$$${a}\:={lim}_{{x}\rightarrow\mathrm{0}} {xF}\left({x}\right)=\frac{−\mathrm{4}}{\left(−\mathrm{2}\right)}\:=\mathrm{2} \\ $$$${b}\:={lim}_{{x}\rightarrow\mathrm{2}} \left({x}−\mathrm{2}\right){F}\left({x}\right)=\frac{\mathrm{6}}{\mathrm{6}}\:=\mathrm{1} \\ $$$${c}\:={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right){F}\left({x}\right)=\:\frac{−\mathrm{3}}{\mathrm{3}}=−\mathrm{1}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{\mathrm{2}}{{x}}\:+\frac{\mathrm{1}}{{x}−\mathrm{2}}\:−\frac{\mathrm{1}}{\left(\boldsymbol{{x}}+\mathrm{1}\right)}\Rightarrow \\ $$$$\int\:{F}\left({x}\right){dx}?=\mathrm{2}{ln}\mid{x}\mid+{ln}\mid{x}−\mathrm{2}\mid−{ln}\mid{x}+\mathrm{1}\mid\:+{c}\:. \\ $$
Answered by afachri last updated on 15/Dec/18
(5) ∫ ((8x+1)/(x(x^2 −6x+9))) dx = ∫((8x+1)/(x(x−3)^2 )) dx = ∫(A/x) + (B/(x−3)) + ((Cx+D)/((x−3)^2 )) dx x = 0 ; x = 3 so A and B are : A = ((8(0)+1)/((0−3)^2 )) = (1/9) ; B = ((8(3)+1)/3) = ((25)/3) eq will be : ∫(1/(9x)) + ((25)/(3(x−3))) + ((Cx+D)/((x−3)^2 )) dx = ∫((8x + 1)/(x(x−3)^2 )) dx (8x+1) = (1/9)(x−3)^2 + ((25)/3)x(x−3) + x(Cx+D) 9(8x+1) = x^2 −6x+9 + 25x^2 −75x + Cx^2 + Dx 9(8x+1) = (1+25+C)x^2 + (−6−75+D)x + 9 look : (1+25+C) = 0 ⇒ C = −26 (−6−75+D) = 72 ⇒ D = 153 ⇒ Cx+D = −26x + 153 so eq : ∫(1/(9x)) + ((25)/(3(x−3))) + ((153−26x)/((x−3)^2 )) = ((ln x)/9) + ((25ln (x−3))/3) + ∫((−26x+153)/((x−3)^2 )) dx •• ∫ ((−26x + 153)/((x−3)^2 )) dxu = x−3 let u = x−3 ⇒ du = dx −26u +75= −26x+78+75 ∫ ((−26u+75)/u^2 ) du = ∫−((26)/u) + ((75)/u^2 ) du = −26 ln u −75u^(−1) = −26 ln (x−3) + ((75)/(x−3)) so the result : = ((ln x)/9) + ((25 ln (x−3))/3) − 26 ln (x−3) + ((75)/(x−3)) + C = ((ln x)/9) − ((53 ln (x−3))/3) + ((75)/(x−3))+ C
$$\left(\mathrm{5}\right)\:\:\int\:\frac{\mathrm{8}{x}+\mathrm{1}}{{x}\left({x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{9}\right)}\:{dx}\:=\:\int\frac{\mathrm{8}{x}+\mathrm{1}}{{x}\left({x}−\mathrm{3}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\int\frac{\mathrm{A}}{{x}}\:\:+\:\:\frac{\mathrm{B}}{{x}−\mathrm{3}}\:+\:\frac{\mathrm{C}{x}+\mathrm{D}}{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }\:{dx} \\ $$$${x}\:=\:\mathrm{0}\:\:;\:\:\:{x}\:=\:\mathrm{3} \\ $$$$\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{A}}\:\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{B}}\:\boldsymbol{\mathrm{are}}\:\::\:\:\mathrm{A}\:=\:\frac{\mathrm{8}\left(\mathrm{0}\right)+\mathrm{1}}{\left(\mathrm{0}−\mathrm{3}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{9}}\:\:\:\:\:;\:\:\:\:\:\:\mathrm{B}\:=\:\frac{\mathrm{8}\left(\mathrm{3}\right)+\mathrm{1}}{\mathrm{3}}\:=\:\frac{\mathrm{25}}{\mathrm{3}} \\ $$$$\boldsymbol{\mathrm{eq}}\:\boldsymbol{\mathrm{will}}\:\boldsymbol{\mathrm{be}}\:\::\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int\frac{\mathrm{1}}{\mathrm{9}{x}}\:+\:\frac{\mathrm{25}}{\mathrm{3}\left({x}−\mathrm{3}\right)}\:+\:\frac{\mathrm{C}{x}+\mathrm{D}}{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }\:{dx}\:=\:\int\frac{\mathrm{8}{x}\:+\:\mathrm{1}}{{x}\left({x}−\mathrm{3}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\left(\mathrm{8}{x}+\mathrm{1}\right)\:\:=\:\:\frac{\mathrm{1}}{\mathrm{9}}\left({x}−\mathrm{3}\right)^{\mathrm{2}} \:+\:\frac{\mathrm{25}}{\mathrm{3}}{x}\left({x}−\mathrm{3}\right)\:+\:{x}\left(\mathrm{C}{x}+\mathrm{D}\right) \\ $$$$\mathrm{9}\left(\mathrm{8}{x}+\mathrm{1}\right)\:=\:{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{9}\:+\:\mathrm{25}{x}^{\mathrm{2}} \:−\mathrm{75}{x}\:+\:\mathrm{C}{x}^{\mathrm{2}} +\:\mathrm{D}{x} \\ $$$$\mathrm{9}\left(\mathrm{8}{x}+\mathrm{1}\right)\:=\:\left(\mathrm{1}+\mathrm{25}+\mathrm{C}\right){x}^{\mathrm{2}} \:+\:\left(−\mathrm{6}−\mathrm{75}+\mathrm{D}\right){x}\:+\:\mathrm{9} \\ $$$$\boldsymbol{\mathrm{look}}\:: \\ $$$$\:\:\:\:\:\:\left(\mathrm{1}+\mathrm{25}+\mathrm{C}\right)\:=\:\mathrm{0}\:\:\:\:\:\:\Rightarrow\:\:\:\:\:\:\mathrm{C}\:=\:−\mathrm{26} \\ $$$$\left(−\mathrm{6}−\mathrm{75}+\mathrm{D}\right)\:=\:\mathrm{72}\:\:\:\Rightarrow\:\:\:\:\:\:\mathrm{D}\:=\:\mathrm{153}\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\:\:\:\mathrm{C}{x}+\mathrm{D}\:=\:−\mathrm{26}{x}\:+\:\mathrm{153} \\ $$$$\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{eq}}\:: \\ $$$$\int\frac{\mathrm{1}}{\mathrm{9}{x}}\:+\:\frac{\mathrm{25}}{\mathrm{3}\left({x}−\mathrm{3}\right)}\:+\:\frac{\mathrm{153}−\mathrm{26}{x}}{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }\:=\:\:\frac{\mathrm{ln}\:{x}}{\mathrm{9}}\:+\:\frac{\mathrm{25ln}\:\left({x}−\mathrm{3}\right)}{\mathrm{3}}\:+\:\int\frac{−\mathrm{26}{x}+\mathrm{153}}{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\bullet\bullet\:\int\:\frac{−\mathrm{26}{x}\:+\:\mathrm{153}}{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }\:{dxu}\:=\:{x}−\mathrm{3} \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{let}}\:\:\:\:\:\:\:\:\:\:{u}\:=\:{x}−\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\:\:\:\:\:\:\:\:{du}\:=\:{dx} \\ $$$$−\mathrm{26}{u}\:+\mathrm{75}=\:−\mathrm{26}{x}+\mathrm{78}+\mathrm{75} \\ $$$$\int\:\frac{−\mathrm{26}{u}+\mathrm{75}}{{u}^{\mathrm{2}} }\:{du}\:\:=\:\:\int−\frac{\mathrm{26}}{{u}}\:\:+\:\:\frac{\mathrm{75}}{{u}^{\mathrm{2}} }\:{du} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\mathrm{26}\:\mathrm{ln}\:{u}\:−\mathrm{75}{u}^{−\mathrm{1}} \: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\mathrm{26}\:\mathrm{ln}\:\left({x}−\mathrm{3}\right)\:+\:\frac{\mathrm{75}}{{x}−\mathrm{3}} \\ $$$$\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{result}}\:: \\ $$$$\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{ln}\:{x}}{\mathrm{9}}\:+\:\frac{\mathrm{25}\:\mathrm{ln}\:\left({x}−\mathrm{3}\right)}{\mathrm{3}}\:−\:\mathrm{26}\:\mathrm{ln}\:\left({x}−\mathrm{3}\right)\:+\:\frac{\mathrm{75}}{{x}−\mathrm{3}}\:+\:{C} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{ln}\:{x}}{\mathrm{9}}\:−\:\frac{\mathrm{53}\:\mathrm{ln}\:\left({x}−\mathrm{3}\right)}{\mathrm{3}}\:+\:\frac{\mathrm{75}}{{x}−\mathrm{3}}+\:{C} \\ $$$$ \\ $$
Commented by Abdo msup. last updated on 24/Dec/18
let I = ∫ ((8x+1)/(x(x^2 −6x+9)))dx ⇒ I =∫ ((8x+1)/(x(x−3)^2 ))dx let devompose F(x)= ((8x+1)/(x(x−3)^2 )) ⇒F(x)= (a/x) +(b/(x−3)) +(c/((x−3)^2 )) a =lim_(x→0) xF(x)=(1/9) c =lim_(x→3) (x−3)^2 F(x)=((25)/3) ⇒ F(x)= (1/(9x)) +(b/(x−3)) +((25)/(3(x−3)^2 )) F(1)=(9/4) =(1/9) −(b/2) +((25)/(12)) ⇒9 =(4/9) −2b +((25)/3) ⇒ 2b =(4/9) +((25)/3) −((27)/3) =(4/9)−(2/3) =((4−6)/9) =−(2/9) ⇒b=−(1/9) F(x)=(1/(9x)) −(1/(9(x−3))) +((25)/(3(x−3)^2 )) ⇒ ∫ F(x)dx =(1/9)ln∣x∣−(1/9)ln∣x−3∣−((25)/(3(x−3))) +c .
$${let}\:{I}\:=\:\:\int\:\:\frac{\mathrm{8}{x}+\mathrm{1}}{{x}\left({x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{9}\right)}{dx}\:\Rightarrow \\ $$$${I}\:=\int\:\frac{\mathrm{8}{x}+\mathrm{1}}{{x}\left({x}−\mathrm{3}\right)^{\mathrm{2}} }{dx}\:{let}\:{devompose} \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{8}{x}+\mathrm{1}}{{x}\left({x}−\mathrm{3}\right)^{\mathrm{2}} }\:\Rightarrow{F}\left({x}\right)=\:\frac{{a}}{{x}}\:+\frac{{b}}{{x}−\mathrm{3}}\:+\frac{{c}}{\left({x}−\mathrm{3}\right)^{\mathrm{2}} } \\ $$$${a}\:={lim}_{{x}\rightarrow\mathrm{0}} {xF}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{9}} \\ $$$${c}\:={lim}_{{x}\rightarrow\mathrm{3}} \left({x}−\mathrm{3}\right)^{\mathrm{2}} {F}\left({x}\right)=\frac{\mathrm{25}}{\mathrm{3}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{9}{x}}\:+\frac{{b}}{{x}−\mathrm{3}}\:+\frac{\mathrm{25}}{\mathrm{3}\left({x}−\mathrm{3}\right)^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{1}\right)=\frac{\mathrm{9}}{\mathrm{4}}\:=\frac{\mathrm{1}}{\mathrm{9}}\:−\frac{{b}}{\mathrm{2}}\:+\frac{\mathrm{25}}{\mathrm{12}}\:\Rightarrow\mathrm{9}\:=\frac{\mathrm{4}}{\mathrm{9}}\:−\mathrm{2}{b}\:+\frac{\mathrm{25}}{\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{2}{b}\:=\frac{\mathrm{4}}{\mathrm{9}}\:+\frac{\mathrm{25}}{\mathrm{3}}\:−\frac{\mathrm{27}}{\mathrm{3}}\:=\frac{\mathrm{4}}{\mathrm{9}}−\frac{\mathrm{2}}{\mathrm{3}}\:=\frac{\mathrm{4}−\mathrm{6}}{\mathrm{9}}\:=−\frac{\mathrm{2}}{\mathrm{9}}\:\Rightarrow{b}=−\frac{\mathrm{1}}{\mathrm{9}} \\ $$$${F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{9}{x}}\:−\frac{\mathrm{1}}{\mathrm{9}\left({x}−\mathrm{3}\right)}\:+\frac{\mathrm{25}}{\mathrm{3}\left({x}−\mathrm{3}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int\:{F}\left({x}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{9}}{ln}\mid{x}\mid−\frac{\mathrm{1}}{\mathrm{9}}{ln}\mid{x}−\mathrm{3}\mid−\frac{\mathrm{25}}{\mathrm{3}\left({x}−\mathrm{3}\right)}\:+{c}\:. \\ $$
Answered by afachri last updated on 15/Dec/18
(6) ∫((5x+7)/(x(x^2 +4x+4))) dx = ∫((5x+7)/(x(x+2)^2 )) dx = ∫ (A/x) + (B/(x+2)) + ((Cx+D)/((x+2)^2 )) dx to define A and B : x = 0 ; x+2 = 0 x = −2 A = ((5(0)+7)/((0+2)^2 )) = (7/4) ; B = ((5(−2)+7)/((−2))) = (3/2) So the eq : ∫ (7/(4x)) + (3/(2(x+2))) + ((Cx+D)/((x+2)^2 )) dx = ∫((5x+7)/(x(x+2)^2 )) dx to define C and D : (( 7(x+2)^2 )/4) + ((3x(x+2))/2) + x(Cx+D) = 5x+7 then multiplied by 4 7(x+2)^2 + 6x(x+2) + 4x(Cx+D) = 20x + 28 (7+6+4C)x^2 + (28+12+4D)x + (28) = 20x+28 observe : (7+6+4C)x^2 = 0x^2 ⇒ C = −((13)/4) (28+12+4D)x = 20x ⇒ D = −5 so , Cx+D = (−((13)/4)x − 5)(4/4) = ((−13x −20)/4) = −((13x+20)/4) eq will be : ∫ (7/(4x)) + (3/(2(x+2))) − (((13x+20))/(4(x+2)^2 )) dx = ((7ln x)/4) + ((3ln (x+2))/2) − ((13ln (x+2))/4) + (6/(4(x+2))) + C = ((7ln x)/4) − ((7ln (x+2))/4) + (3/(2(x+2))) + C = (7/4)[ ln ((x/(x+2))) ] + (3/(2(x+2))) + C
$$\left(\mathrm{6}\right)\:\:\int\frac{\mathrm{5}{x}+\mathrm{7}}{{x}\left({x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}\right)}\:{dx}\:\:=\:\:\:\int\frac{\mathrm{5}{x}+\mathrm{7}}{{x}\left({x}+\mathrm{2}\right)^{\mathrm{2}} }\:{dx}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\int\:\frac{\mathrm{A}}{{x}}\:\:+\:\:\frac{\mathrm{B}}{{x}+\mathrm{2}}\:\:+\:\:\frac{\mathrm{C}{x}+\mathrm{D}}{\left({x}+\mathrm{2}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\mathrm{to}\:\mathrm{define}\:\boldsymbol{\mathrm{A}}\:\mathrm{and}\:\boldsymbol{\mathrm{B}}\:: \\ $$$$\:\:\:{x}\:=\:\mathrm{0}\:\:\:\:\:;\:\:\:\:\:{x}+\mathrm{2}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\:=\:−\mathrm{2} \\ $$$$\:\:\:\mathrm{A}\:=\:\frac{\mathrm{5}\left(\mathrm{0}\right)+\mathrm{7}}{\left(\mathrm{0}+\mathrm{2}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{7}}{\mathrm{4}}\:\:\:\:\:\:\:\:;\:\:\:\:\:\:\:\:\mathrm{B}\:=\:\frac{\mathrm{5}\left(−\mathrm{2}\right)+\mathrm{7}}{\left(−\mathrm{2}\right)}\:=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{So}\:\mathrm{the}\:\mathrm{eq}\:: \\ $$$$\:\:\int\:\frac{\mathrm{7}}{\mathrm{4}{x}}\:+\:\frac{\mathrm{3}}{\mathrm{2}\left({x}+\mathrm{2}\right)}\:+\:\frac{\mathrm{C}{x}+\mathrm{D}}{\left({x}+\mathrm{2}\right)^{\mathrm{2}} }\:{dx}\:\:=\:\:\int\frac{\mathrm{5}{x}+\mathrm{7}}{{x}\left({x}+\mathrm{2}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\mathrm{to}\:\mathrm{define}\:\boldsymbol{\mathrm{C}}\:\mathrm{and}\:\boldsymbol{\mathrm{D}}\:\:: \\ $$$$\:\:\:\frac{\:\mathrm{7}\left({x}+\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{4}}\:+\:\frac{\mathrm{3}{x}\left({x}+\mathrm{2}\right)}{\mathrm{2}}\:+\:{x}\left(\mathrm{C}{x}+\mathrm{D}\right)\:\:\:\:=\:\:\mathrm{5}{x}+\mathrm{7}\:\:\:\:\:\boldsymbol{\mathrm{then}}\:\boldsymbol{\mathrm{multiplied}}\:\boldsymbol{\mathrm{by}}\:\mathrm{4} \\ $$$$\:\:\mathrm{7}\left({x}+\mathrm{2}\right)^{\mathrm{2}} \:+\:\mathrm{6}{x}\left({x}+\mathrm{2}\right)\:+\:\mathrm{4}{x}\left(\mathrm{C}{x}+\mathrm{D}\right)\:\:\:=\:\mathrm{20}{x}\:+\:\mathrm{28} \\ $$$$\left(\mathrm{7}+\mathrm{6}+\mathrm{4C}\right){x}^{\mathrm{2}} +\:\left(\mathrm{28}+\mathrm{12}+\mathrm{4D}\right){x}\:+\:\left(\mathrm{28}\right)\:\:\:=\:\:\mathrm{20}{x}+\mathrm{28}\: \\ $$$$\boldsymbol{\mathrm{observe}}\:: \\ $$$$\:\:\:\:\:\left(\mathrm{7}+\mathrm{6}+\mathrm{4C}\right){x}^{\mathrm{2}} \:=\:\:\mathrm{0}{x}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\:\:\:\:\:\:\:\:\mathrm{C}\:=\:−\frac{\mathrm{13}}{\mathrm{4}} \\ $$$$\left(\mathrm{28}+\mathrm{12}+\mathrm{4D}\right){x}\:\:=\:\:\mathrm{20}{x}\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\:\:\:\:\:\:\:\:\mathrm{D}\:=\:−\mathrm{5} \\ $$$$\boldsymbol{\mathrm{so}}\:,\:\:\:\mathrm{C}{x}+\mathrm{D}\:\:=\:\:\left(−\frac{\mathrm{13}}{\mathrm{4}}{x}\:−\:\mathrm{5}\right)\frac{\mathrm{4}}{\mathrm{4}}\:\:=\:\frac{−\mathrm{13}{x}\:−\mathrm{20}}{\mathrm{4}}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:−\frac{\mathrm{13}{x}+\mathrm{20}}{\mathrm{4}} \\ $$$$\boldsymbol{\mathrm{eq}}\:\boldsymbol{\mathrm{will}}\:\boldsymbol{\mathrm{be}}\:\::\:\:\int\:\frac{\mathrm{7}}{\mathrm{4}{x}}\:+\:\frac{\mathrm{3}}{\mathrm{2}\left({x}+\mathrm{2}\right)}\:−\:\frac{\left(\mathrm{13}{x}+\mathrm{20}\right)}{\mathrm{4}\left({x}+\mathrm{2}\right)^{\mathrm{2}} }\:\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\frac{\mathrm{7ln}\:{x}}{\mathrm{4}}\:\:+\:\:\frac{\mathrm{3ln}\:\left({x}+\mathrm{2}\right)}{\mathrm{2}}\:\:−\:\:\frac{\mathrm{13ln}\:\left({x}+\mathrm{2}\right)}{\mathrm{4}}\:\:+\:\frac{\mathrm{6}}{\mathrm{4}\left({x}+\mathrm{2}\right)}\:\:+\:\:{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\frac{\mathrm{7ln}\:{x}}{\mathrm{4}}\:\:−\:\:\frac{\mathrm{7ln}\:\left({x}+\mathrm{2}\right)}{\mathrm{4}}\:\:+\:\:\frac{\mathrm{3}}{\mathrm{2}\left({x}+\mathrm{2}\right)}\:\:+\:\:{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\frac{\mathrm{7}}{\mathrm{4}}\left[\:\mathrm{ln}\:\left(\frac{{x}}{{x}+\mathrm{2}}\right)\:\right]\:\:+\:\:\frac{\mathrm{3}}{\mathrm{2}\left({x}+\mathrm{2}\right)}\:\:+\:\:{C} \\ $$$$ \\ $$
Commented by cesar.marval.larez@gmail.com last updated on 15/Dec/18
with u i am learning more. i have master other country
$${with}\:{u}\:{i}\:{am}\:{learning}\:{more}.\:{i}\:{have}\:{master} \\ $$$${other}\:{country} \\ $$
Commented by afachri last updated on 15/Dec/18
hehehe i′m not that good my friend. i am still a student. we can share and cmplete each other here :) Glad to give a friend a hand :)
$$\mathrm{hehehe}\:\mathrm{i}'\mathrm{m}\:\mathrm{not}\:\mathrm{that}\:\mathrm{good}\:\mathrm{my}\:\mathrm{friend}.\:\mathrm{i}\:\mathrm{am} \\ $$$$\mathrm{still}\:\mathrm{a}\:\mathrm{student}.\:\mathrm{we}\:\mathrm{can}\:\mathrm{share}\:\mathrm{and}\:\mathrm{cmplete} \\ $$$$\left.\mathrm{each}\:\mathrm{other}\:\mathrm{here}\::\right)\:\mathrm{Glad}\:\mathrm{to}\:\mathrm{give}\:\mathrm{a}\:\mathrm{friend} \\ $$$$\left.\mathrm{a}\:\mathrm{hand}\::\right) \\ $$
Commented by afachri last updated on 15/Dec/18
waw it′s great sir. i′ll text you. i′m Indonesian.
$$\mathrm{waw}\:\mathrm{it}'\mathrm{s}\:\mathrm{great}\:\mathrm{sir}.\:\mathrm{i}'\mathrm{ll}\:\mathrm{text}\:\mathrm{you}.\:\mathrm{i}'\mathrm{m}\:\mathrm{Indonesian}. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *