Question Number 50248 by peter frank last updated on 15/Dec/18

Answered by mr W last updated on 15/Dec/18
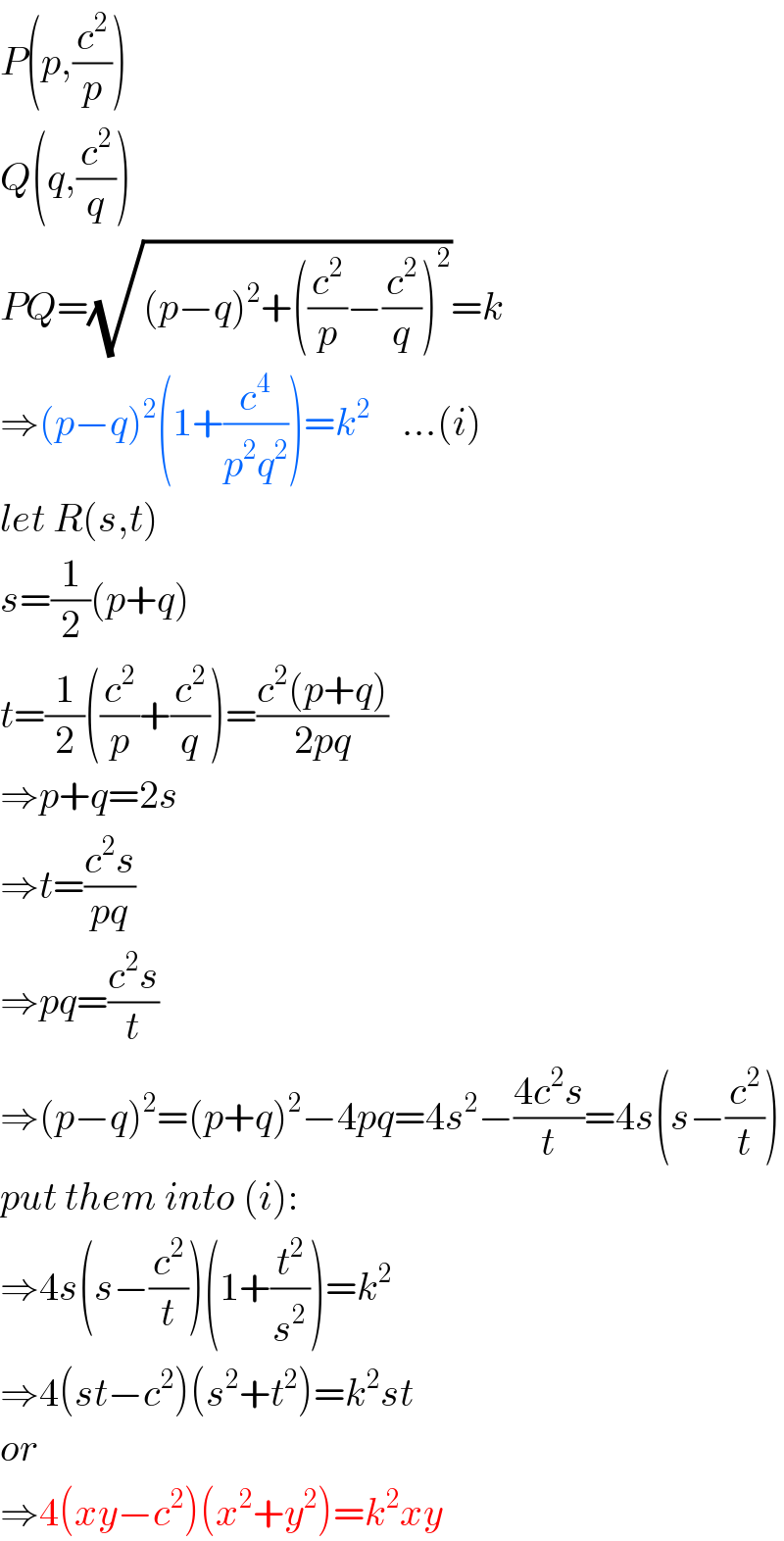
$${P}\left({p},\frac{{c}^{\mathrm{2}} }{{p}}\right) \\ $$$${Q}\left({q},\frac{{c}^{\mathrm{2}} }{{q}}\right) \\ $$$${PQ}=\sqrt{\left({p}−{q}\right)^{\mathrm{2}} +\left(\frac{{c}^{\mathrm{2}} }{{p}}−\frac{{c}^{\mathrm{2}} }{{q}}\right)^{\mathrm{2}} }={k} \\ $$$$\Rightarrow\left({p}−{q}\right)^{\mathrm{2}} \left(\mathrm{1}+\frac{{c}^{\mathrm{4}} }{{p}^{\mathrm{2}} {q}^{\mathrm{2}} }\right)={k}^{\mathrm{2}} \:\:\:\:…\left({i}\right) \\ $$$${let}\:{R}\left({s},{t}\right) \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{2}}\left({p}+{q}\right) \\ $$$${t}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{c}^{\mathrm{2}} }{{p}}+\frac{{c}^{\mathrm{2}} }{{q}}\right)=\frac{{c}^{\mathrm{2}} \left({p}+{q}\right)}{\mathrm{2}{pq}} \\ $$$$\Rightarrow{p}+{q}=\mathrm{2}{s} \\ $$$$\Rightarrow{t}=\frac{{c}^{\mathrm{2}} {s}}{{pq}} \\ $$$$\Rightarrow{pq}=\frac{{c}^{\mathrm{2}} {s}}{{t}} \\ $$$$\Rightarrow\left({p}−{q}\right)^{\mathrm{2}} =\left({p}+{q}\right)^{\mathrm{2}} −\mathrm{4}{pq}=\mathrm{4}{s}^{\mathrm{2}} −\frac{\mathrm{4}{c}^{\mathrm{2}} {s}}{{t}}=\mathrm{4}{s}\left({s}−\frac{{c}^{\mathrm{2}} }{{t}}\right) \\ $$$${put}\:{them}\:{into}\:\left({i}\right): \\ $$$$\Rightarrow\mathrm{4}{s}\left({s}−\frac{{c}^{\mathrm{2}} }{{t}}\right)\left(\mathrm{1}+\frac{{t}^{\mathrm{2}} }{{s}^{\mathrm{2}} }\right)={k}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}\left({st}−{c}^{\mathrm{2}} \right)\left({s}^{\mathrm{2}} +{t}^{\mathrm{2}} \right)={k}^{\mathrm{2}} {st} \\ $$$${or} \\ $$$$\Rightarrow\mathrm{4}\left({xy}−{c}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)={k}^{\mathrm{2}} {xy} \\ $$
Commented by mr W last updated on 15/Dec/18

Commented by peter frank last updated on 16/Dec/18
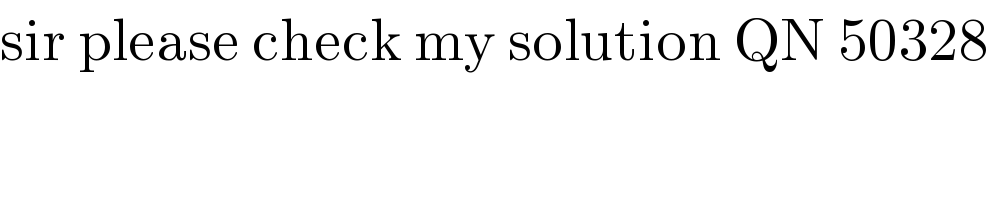
$$\mathrm{sir}\:\mathrm{please}\:\mathrm{check}\:\mathrm{my}\:\mathrm{solution}\:\mathrm{QN}\:\mathrm{50328} \\ $$
