Question Number 50274 by Tawa1 last updated on 15/Dec/18

Answered by tanmay.chaudhury50@gmail.com last updated on 15/Dec/18
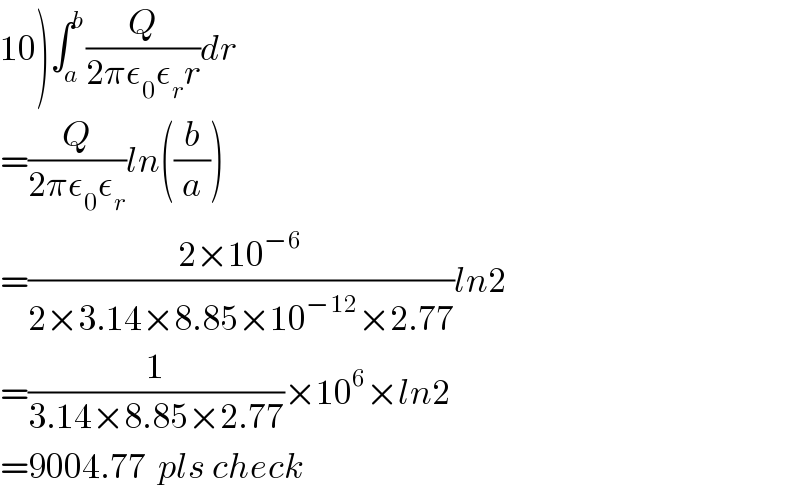
$$\left.\mathrm{10}\right)\int_{{a}} ^{{b}} \frac{{Q}}{\mathrm{2}\pi\epsilon_{\mathrm{0}} \epsilon_{{r}} {r}}{dr} \\ $$$$=\frac{{Q}}{\mathrm{2}\pi\epsilon_{\mathrm{0}} \epsilon_{{r}} }{ln}\left(\frac{{b}}{{a}}\right) \\ $$$$=\frac{\mathrm{2}×\mathrm{10}^{−\mathrm{6}} }{\mathrm{2}×\mathrm{3}.\mathrm{14}×\mathrm{8}.\mathrm{85}×\mathrm{10}^{−\mathrm{12}} ×\mathrm{2}.\mathrm{77}}{ln}\mathrm{2} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}.\mathrm{14}×\mathrm{8}.\mathrm{85}×\mathrm{2}.\mathrm{77}}×\mathrm{10}^{\mathrm{6}} ×{ln}\mathrm{2} \\ $$$$=\mathrm{9004}.\mathrm{77}\:\:{pls}\:{check} \\ $$
Commented by Tawa1 last updated on 15/Dec/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Dec/18
![11)=(1/π)∫_0 ^π [10sinwt+3sin3wt+2sin5wt]d(wt) =((−1)/π)∣10×((coswt)/1)+3×((cos3wt)/3)+2×((cos5wt)/5)∣_0 ^π =((−1)/π)[10(cosπ−cos0)+(cos3π−cos0)+(2/5)(cos5π−cos0)] =((−1)/π)[10(−1−1)+(−1−1)+(2/5)(−1−1)] =((−1)/π)[(−2)(10+1+(2/5))] =(2/π)×((57)/5)=((114)/(5π)) =7.26](https://www.tinkutara.com/question/Q50291.png)
$$\left.\mathrm{11}\right)=\frac{\mathrm{1}}{\pi}\int_{\mathrm{0}} ^{\pi} \left[\mathrm{10}{sinwt}+\mathrm{3}{sin}\mathrm{3}{wt}+\mathrm{2}{sin}\mathrm{5}{wt}\right]{d}\left({wt}\right) \\ $$$$=\frac{−\mathrm{1}}{\pi}\mid\mathrm{10}×\frac{{coswt}}{\mathrm{1}}+\mathrm{3}×\frac{{cos}\mathrm{3}{wt}}{\mathrm{3}}+\mathrm{2}×\frac{{cos}\mathrm{5}{wt}}{\mathrm{5}}\mid_{\mathrm{0}} ^{\pi} \\ $$$$=\frac{−\mathrm{1}}{\pi}\left[\mathrm{10}\left({cos}\pi−{cos}\mathrm{0}\right)+\left({cos}\mathrm{3}\pi−{cos}\mathrm{0}\right)+\frac{\mathrm{2}}{\mathrm{5}}\left({cos}\mathrm{5}\pi−{cos}\mathrm{0}\right)\right] \\ $$$$=\frac{−\mathrm{1}}{\pi}\left[\mathrm{10}\left(−\mathrm{1}−\mathrm{1}\right)+\left(−\mathrm{1}−\mathrm{1}\right)+\frac{\mathrm{2}}{\mathrm{5}}\left(−\mathrm{1}−\mathrm{1}\right)\right] \\ $$$$=\frac{−\mathrm{1}}{\pi}\left[\left(−\mathrm{2}\right)\left(\mathrm{10}+\mathrm{1}+\frac{\mathrm{2}}{\mathrm{5}}\right)\right] \\ $$$$=\frac{\mathrm{2}}{\pi}×\frac{\mathrm{57}}{\mathrm{5}}=\frac{\mathrm{114}}{\mathrm{5}\pi} \\ $$$$=\mathrm{7}.\mathrm{26} \\ $$
Commented by Tawa1 last updated on 15/Dec/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir} \\ $$
