Question Number 50275 by Tawa1 last updated on 15/Dec/18

Answered by tanmay.chaudhury50@gmail.com last updated on 15/Dec/18
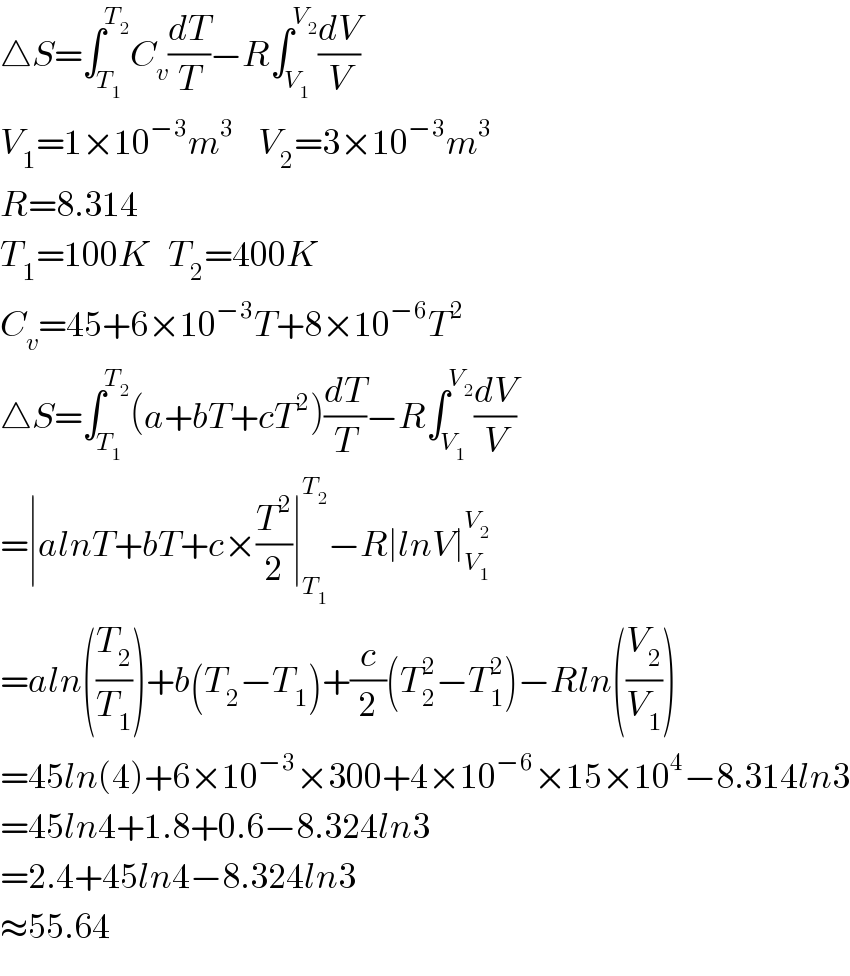
$$\bigtriangleup{S}=\int_{{T}_{\mathrm{1}} } ^{{T}_{\mathrm{2}} } {C}_{{v}} \frac{{dT}}{{T}}−{R}\int_{{V}_{\mathrm{1}} } ^{{V}_{\mathrm{2}} } \frac{{dV}}{{V}} \\ $$$${V}_{\mathrm{1}} =\mathrm{1}×\mathrm{10}^{−\mathrm{3}} {m}^{\mathrm{3}} \:\:\:\:{V}_{\mathrm{2}} =\mathrm{3}×\mathrm{10}^{−\mathrm{3}} {m}^{\mathrm{3}} \\ $$$${R}=\mathrm{8}.\mathrm{314} \\ $$$${T}_{\mathrm{1}} =\mathrm{100}{K}\:\:\:{T}_{\mathrm{2}} =\mathrm{400}{K} \\ $$$${C}_{{v}} =\mathrm{45}+\mathrm{6}×\mathrm{10}^{−\mathrm{3}} {T}+\mathrm{8}×\mathrm{10}^{−\mathrm{6}} {T}^{\mathrm{2}} \\ $$$$\bigtriangleup{S}=\int_{{T}_{\mathrm{1}} } ^{{T}_{\mathrm{2}} } \left({a}+{bT}+{cT}^{\mathrm{2}} \right)\frac{{dT}}{{T}}−{R}\int_{{V}_{\mathrm{1}} } ^{{V}_{\mathrm{2}} } \frac{{dV}}{{V}} \\ $$$$=\mid{alnT}+{bT}+{c}×\frac{{T}^{\mathrm{2}} }{\mathrm{2}}\mid_{{T}_{\mathrm{1}} } ^{{T}_{\mathrm{2}} } −{R}\mid{lnV}\mid_{{V}_{\mathrm{1}} } ^{{V}_{\mathrm{2}} } \\ $$$$={aln}\left(\frac{{T}_{\mathrm{2}} }{{T}_{\mathrm{1}} }\right)+{b}\left({T}_{\mathrm{2}} −{T}_{\mathrm{1}} \right)+\frac{{c}}{\mathrm{2}}\left({T}_{\mathrm{2}} ^{\mathrm{2}} −{T}_{\mathrm{1}} ^{\mathrm{2}} \right)−{Rln}\left(\frac{{V}_{\mathrm{2}} }{{V}_{\mathrm{1}} }\right) \\ $$$$=\mathrm{45}{ln}\left(\mathrm{4}\right)+\mathrm{6}×\mathrm{10}^{−\mathrm{3}} ×\mathrm{300}+\mathrm{4}×\mathrm{10}^{−\mathrm{6}} ×\mathrm{15}×\mathrm{10}^{\mathrm{4}} −\mathrm{8}.\mathrm{314}{ln}\mathrm{3} \\ $$$$=\mathrm{45}{ln}\mathrm{4}+\mathrm{1}.\mathrm{8}+\mathrm{0}.\mathrm{6}−\mathrm{8}.\mathrm{324}{ln}\mathrm{3} \\ $$$$=\mathrm{2}.\mathrm{4}+\mathrm{45}{ln}\mathrm{4}−\mathrm{8}.\mathrm{324}{ln}\mathrm{3} \\ $$$$\approx\mathrm{55}.\mathrm{64} \\ $$
Commented by Tawa1 last updated on 15/Dec/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
