Question Number 50460 by ajfour last updated on 16/Dec/18
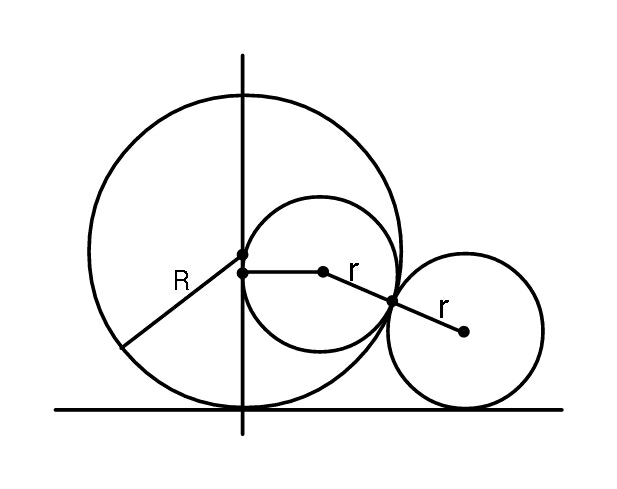
Commented by ajfour last updated on 16/Dec/18
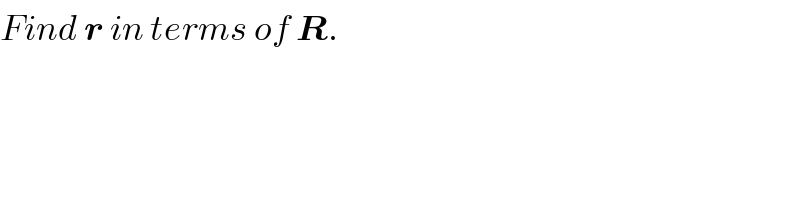
$${Find}\:\boldsymbol{{r}}\:{in}\:{terms}\:{of}\:\boldsymbol{{R}}. \\ $$
Commented by MJS last updated on 18/Dec/18
![I solved this for 2 small circles with r=1 and . a parabola y=ax^2 . a circle x^2 +(y−r)^2 =r^2 . an ellipse (x^2 /a^2 )+(((y−b)^2 )/b^2 )=1 [this one is tricky, will post soon] will also try for a hyperbola](https://www.tinkutara.com/question/Q50655.png)
$$\mathrm{I}\:\mathrm{solved}\:\mathrm{this}\:\mathrm{for}\:\mathrm{2}\:\mathrm{small}\:\mathrm{circles}\:\mathrm{with}\:{r}=\mathrm{1}\:\mathrm{and} \\ $$$$.\:\mathrm{a}\:\mathrm{parabola}\:{y}={ax}^{\mathrm{2}} \\ $$$$.\:\mathrm{a}\:\mathrm{circle}\:{x}^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$.\:\mathrm{an}\:\mathrm{ellipse}\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}−{b}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\:\:\:\:\:\left[\mathrm{this}\:\mathrm{one}\:\mathrm{is}\:\mathrm{tricky},\:\mathrm{will}\:\mathrm{post}\:\mathrm{soon}\right] \\ $$$$\mathrm{will}\:\mathrm{also}\:\mathrm{try}\:\mathrm{for}\:\mathrm{a}\:\mathrm{hyperbola} \\ $$
Answered by mr W last updated on 16/Dec/18
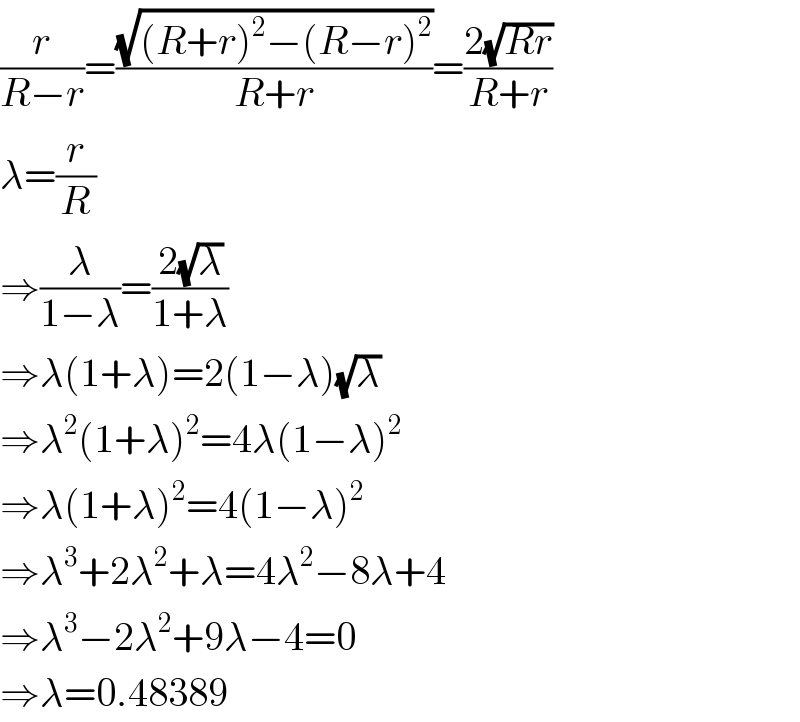
$$\frac{{r}}{{R}−{r}}=\frac{\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} }}{{R}+{r}}=\frac{\mathrm{2}\sqrt{{Rr}}}{{R}+{r}} \\ $$$$\lambda=\frac{{r}}{{R}} \\ $$$$\Rightarrow\frac{\lambda}{\mathrm{1}−\lambda}=\frac{\mathrm{2}\sqrt{\lambda}}{\mathrm{1}+\lambda} \\ $$$$\Rightarrow\lambda\left(\mathrm{1}+\lambda\right)=\mathrm{2}\left(\mathrm{1}−\lambda\right)\sqrt{\lambda} \\ $$$$\Rightarrow\lambda^{\mathrm{2}} \left(\mathrm{1}+\lambda\right)^{\mathrm{2}} =\mathrm{4}\lambda\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} \\ $$$$\Rightarrow\lambda\left(\mathrm{1}+\lambda\right)^{\mathrm{2}} =\mathrm{4}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} \\ $$$$\Rightarrow\lambda^{\mathrm{3}} +\mathrm{2}\lambda^{\mathrm{2}} +\lambda=\mathrm{4}\lambda^{\mathrm{2}} −\mathrm{8}\lambda+\mathrm{4} \\ $$$$\Rightarrow\lambda^{\mathrm{3}} −\mathrm{2}\lambda^{\mathrm{2}} +\mathrm{9}\lambda−\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow\lambda=\mathrm{0}.\mathrm{48389} \\ $$
Commented by ajfour last updated on 16/Dec/18
$${Thanks}\:{for}\:{solving}\:{Sir}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18
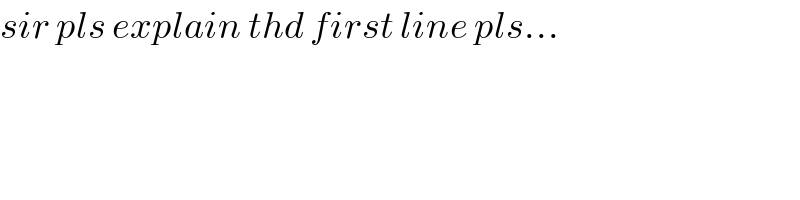
$${sir}\:{pls}\:{explain}\:{thd}\:{first}\:{line}\:{pls}… \\ $$
Commented by mr W last updated on 17/Dec/18
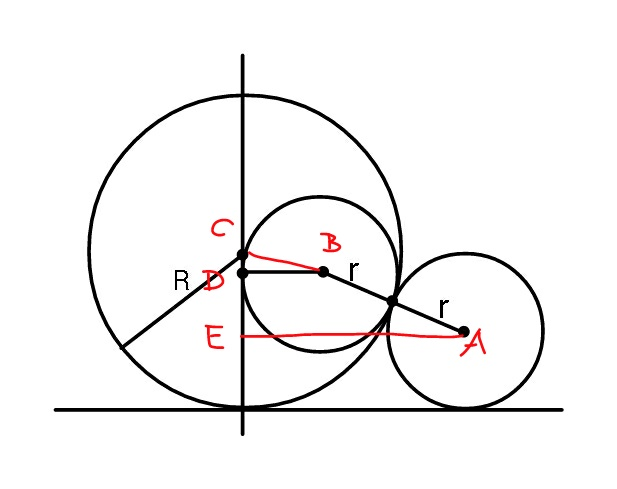
Commented by mr W last updated on 17/Dec/18
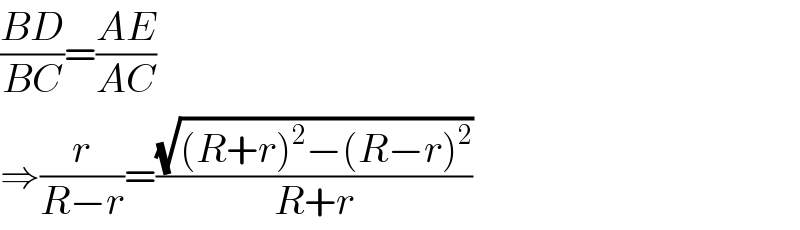
$$\frac{{BD}}{{BC}}=\frac{{AE}}{{AC}} \\ $$$$\Rightarrow\frac{{r}}{{R}−{r}}=\frac{\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} }}{{R}+{r}} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18
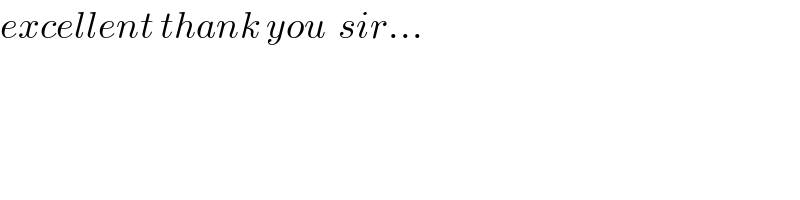
$${excellent}\:{thank}\:{you}\:\:{sir}… \\ $$
Commented by ajfour last updated on 17/Dec/18
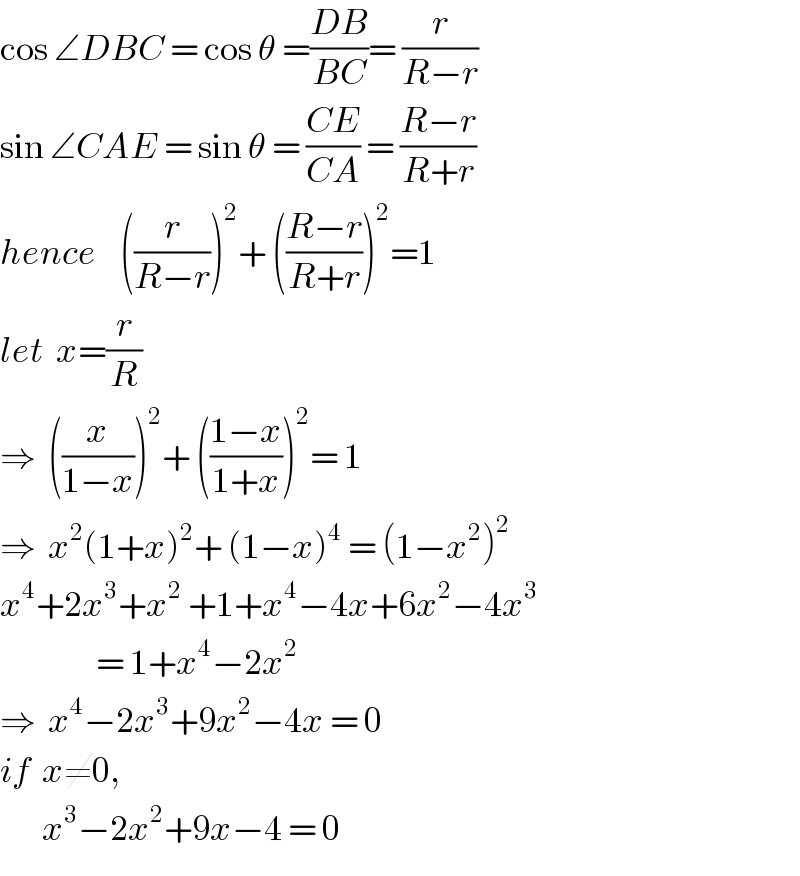
$$\mathrm{cos}\:\angle{DBC}\:=\:\mathrm{cos}\:\theta\:=\frac{{DB}}{{BC}}=\:\frac{{r}}{{R}−{r}} \\ $$$$\mathrm{sin}\:\angle{CAE}\:=\:\mathrm{sin}\:\theta\:=\:\frac{{CE}}{{CA}}\:=\:\frac{{R}−{r}}{{R}+{r}} \\ $$$${hence}\:\:\:\:\left(\frac{{r}}{{R}−{r}}\right)^{\mathrm{2}} +\:\left(\frac{{R}−{r}}{{R}+{r}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${let}\:\:{x}=\frac{{r}}{{R}} \\ $$$$\Rightarrow\:\:\left(\frac{{x}}{\mathrm{1}−{x}}\right)^{\mathrm{2}} +\:\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)^{\mathrm{2}} =\:\mathrm{1} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)^{\mathrm{2}} +\:\left(\mathrm{1}−{x}\right)^{\mathrm{4}} \:=\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} \:+\mathrm{1}+{x}^{\mathrm{4}} −\mathrm{4}{x}+\mathrm{6}{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}+{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{2}} −\mathrm{4}{x}\:=\:\mathrm{0} \\ $$$${if}\:\:{x}\neq\mathrm{0}, \\ $$$$\:\:\:\:\:\:\:{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{9}{x}−\mathrm{4}\:=\:\mathrm{0} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18

$${thank}\:{you}\:{sir}… \\ $$
Answered by ajfour last updated on 16/Dec/18

$${i}\:{get}\:{r}=\:\mathrm{0}.\mathrm{48389}{R} \\ $$
Commented by peter frank last updated on 16/Dec/18
$${please}\:\:{help}\:{QN}\:\mathrm{50349} \\ $$
Commented by ajfour last updated on 16/Dec/18
$${thanks}\:{Sir}!\:{for}\:{confirming}. \\ $$
Commented by MJS last updated on 16/Dec/18

$$\mathrm{me}\:\mathrm{too}. \\ $$$$\mathrm{I}'\mathrm{ve}\:\mathrm{been}\:\mathrm{trying}\:\mathrm{with}\:\mathrm{an}\:\mathrm{ellipse}\:\mathrm{instead}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{big}\:\mathrm{circle},\:\mathrm{it}\:\mathrm{seems}\:\mathrm{very}\:\mathrm{hard}…\:\mathrm{not}\:\mathrm{sure} \\ $$$$\mathrm{if}\:\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{solve}. \\ $$
