Question Number 50568 by ajfour last updated on 17/Dec/18
Commented by ajfour last updated on 17/Dec/18
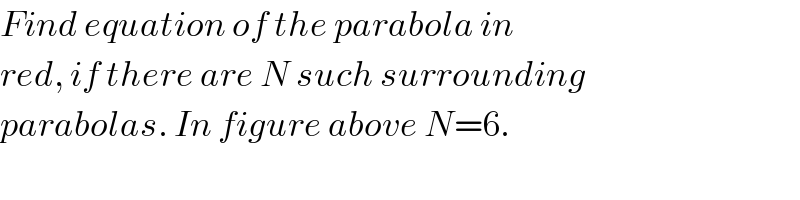
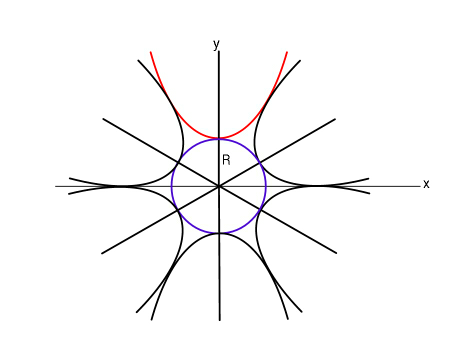
$${Find}\:{equation}\:{of}\:{the}\:{parabola}\:{in} \\ $$$${red},\:{if}\:{there}\:{are}\:{N}\:{such}\:{surrounding} \\ $$$${parabolas}.\:{In}\:{figure}\:{above}\:{N}=\mathrm{6}. \\ $$
Answered by mr W last updated on 17/Dec/18

$${let}\:{y}={ax}^{\mathrm{2}} +{R} \\ $$$$\theta=\frac{\mathrm{2}\pi}{\mathrm{2}{n}}=\frac{\pi}{{n}} \\ $$$${y}=\frac{{x}}{\mathrm{tan}\:\theta} \\ $$$${ax}^{\mathrm{2}} −\frac{{x}}{\mathrm{tan}\:\theta}+{R}=\mathrm{0} \\ $$$${D}=\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\theta}−\mathrm{4}{aR}=\mathrm{0} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{4}{R}\:\mathrm{tan}^{\mathrm{2}} \:\theta} \\ $$$$\Rightarrow{eqn}.\:{of}\:{parabola} \\ $$$${y}=\frac{{x}^{\mathrm{2}} }{\mathrm{4}{R}\:\mathrm{tan}^{\mathrm{2}} \:\frac{\pi}{{n}}}+{R} \\ $$
Commented by ajfour last updated on 17/Dec/18

$${Very}\:{Nice}\:{Sir}!\: \\ $$
