Question-50577

Question Number 50577 by behi83417@gmail.com last updated on 17/Dec/18

Commented by behi83417@gmail.com last updated on 17/Dec/18

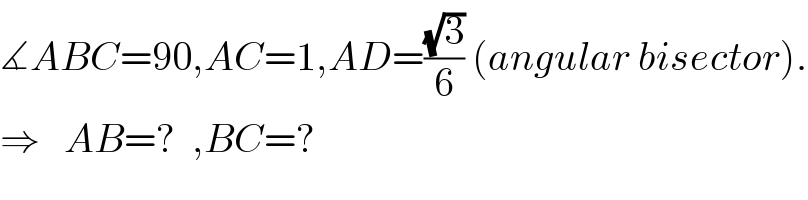
∡ABC=90,AC=1,AD=((√3)/6) (angular bisector). ⇒ AB=? ,BC=?

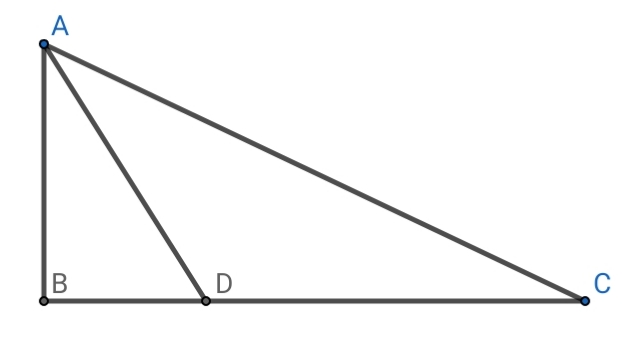
$$\measuredangle{ABC}=\mathrm{90},{AC}=\mathrm{1},{AD}=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\:\left({angular}\:{bisector}\right). \\ $$$$\Rightarrow\:\:\:{AB}=?\:\:,{BC}=? \\ $$

Answered by ajfour last updated on 17/Dec/18

let ∠BAC = 2θ , BC = sin 2θ AB = cos 2θ , AD = cos 2θsec θ AD = ((cos 2θ)/(cos θ)) = (1/(2(√3))) ⇒ 2cos^2 θ−1−((cos θ)/(2(√3))) = 0 4cos θ = (1/(2(√3)))+(√((1/(12))+8)) = (((√(97))+1)/(8(√3))) AB = cos 2θ = ((cos θ)/(2(√3))) = (((√(97))+1)/(48)) AB ≈ 0.226 BC = (√(1−((((√(97))+1)/(48)))^2 )) ≈ 0.974

$${let}\:\:\angle{BAC}\:=\:\mathrm{2}\theta\:\:,\:{BC}\:=\:\mathrm{sin}\:\mathrm{2}\theta \\ $$$${AB}\:=\:\mathrm{cos}\:\mathrm{2}\theta\:\:,\:{AD}\:=\:\mathrm{cos}\:\mathrm{2}\theta\mathrm{sec}\:\theta \\ $$$${AD}\:=\:\frac{\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{cos}\:\theta}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\:\:\:\:\:\mathrm{2cos}\:^{\mathrm{2}} \theta−\mathrm{1}−\frac{\mathrm{cos}\:\theta}{\mathrm{2}\sqrt{\mathrm{3}}}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\mathrm{4cos}\:\theta\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}+\sqrt{\frac{\mathrm{1}}{\mathrm{12}}+\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{97}}+\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{3}}}\:\: \\ $$$$\:{AB}\:=\:\mathrm{cos}\:\mathrm{2}\theta\:=\:\frac{\mathrm{cos}\:\theta}{\mathrm{2}\sqrt{\mathrm{3}}}\:=\:\frac{\sqrt{\mathrm{97}}+\mathrm{1}}{\mathrm{48}}\: \\ $$$$\:\:\:\:\:\:{AB}\:\approx\:\mathrm{0}.\mathrm{226} \\ $$$$\:\:\:{BC}\:=\:\sqrt{\mathrm{1}−\left(\frac{\sqrt{\mathrm{97}}+\mathrm{1}}{\mathrm{48}}\right)^{\mathrm{2}} }\:\:\:\approx\:\mathrm{0}.\mathrm{974}\: \\ $$

Commented by behi83417@gmail.com last updated on 17/Dec/18

$${thanks}\:{sir}\:{Ajfour}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply