Question-50676

Question Number 50676 by Tinkutara last updated on 18/Dec/18

Commented by ajfour last updated on 18/Dec/18

Commented by ajfour last updated on 18/Dec/18

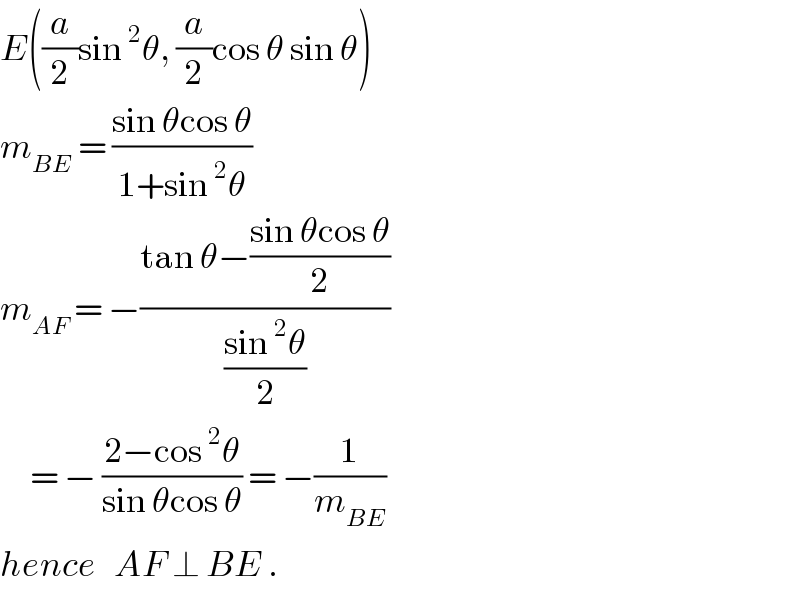
E((a/2)sin^2 θ, (a/2)cos θ sin θ) m_(BE) = ((sin θcos θ)/(1+sin^2 θ)) m_(AF) = −((tan θ−((sin θcos θ)/2))/((sin^2 θ)/2)) = − ((2−cos^2 θ)/(sin θcos θ)) = −(1/m_(BE) ) hence AF ⊥ BE .

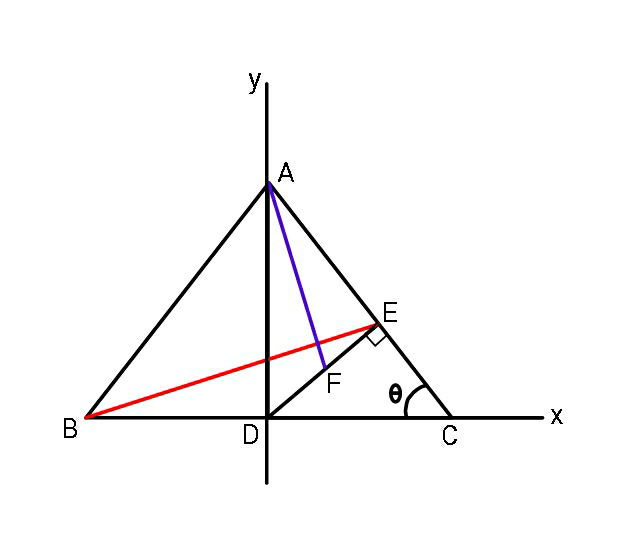
$${E}\left(\frac{{a}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \theta,\:\frac{{a}}{\mathrm{2}}\mathrm{cos}\:\theta\:\mathrm{sin}\:\theta\right) \\ $$$${m}_{{BE}} \:=\:\frac{\mathrm{sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \theta} \\ $$$${m}_{{AF}} \:=\:−\frac{\mathrm{tan}\:\theta−\frac{\mathrm{sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{2}}}{\frac{\mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{2}}} \\ $$$$\:\:\:\:\:=\:−\:\frac{\mathrm{2}−\mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{sin}\:\theta\mathrm{cos}\:\theta}\:=\:−\frac{\mathrm{1}}{{m}_{{BE}} } \\ $$$${hence}\:\:\:{AF}\:\bot\:{BE}\:. \\ $$

Commented by Tinkutara last updated on 19/Dec/18

Thanks Sir! Excellent method, simple and short!

Facebook Tweet Pin

Question-50676

Leave a Reply Cancel reply