Question-50717

Question Number 50717 by Tawa1 last updated on 19/Dec/18

Answered by tanmay.chaudhury50@gmail.com last updated on 19/Dec/18

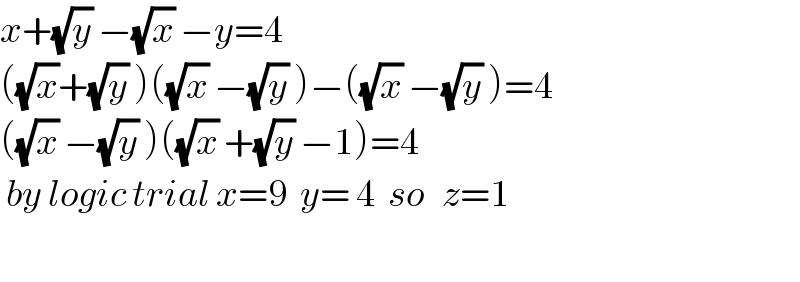
x+(√y) −(√x) −y=4 ((√x)+(√y) )((√x) −(√y) )−((√x) −(√y) )=4 ((√x) −(√y) )((√x) +(√y) −1)=4 by logic trial x=9 y= 4 so z=1

$${x}+\sqrt{{y}}\:−\sqrt{{x}}\:−{y}=\mathrm{4} \\ $$$$\left(\sqrt{{x}}+\sqrt{{y}}\:\right)\left(\sqrt{{x}}\:−\sqrt{{y}}\:\right)−\left(\sqrt{{x}}\:−\sqrt{{y}}\:\right)=\mathrm{4} \\ $$$$\left(\sqrt{{x}}\:−\sqrt{{y}}\:\right)\left(\sqrt{{x}}\:+\sqrt{{y}}\:−\mathrm{1}\right)=\mathrm{4} \\ $$$$\:{by}\:{logic}\:{trial}\:{x}=\mathrm{9}\:\:{y}=\:\mathrm{4}\:\:{so}\:\:\:{z}=\mathrm{1} \\ $$$$ \\ $$

Commented by Tawa1 last updated on 19/Dec/18

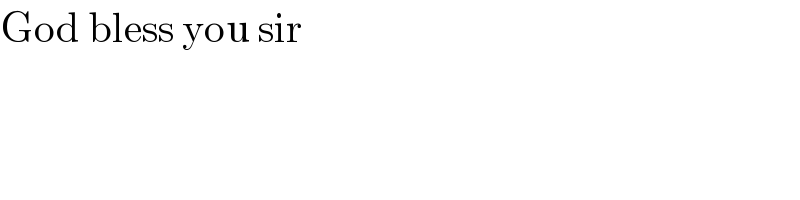
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by ajfour last updated on 19/Dec/18

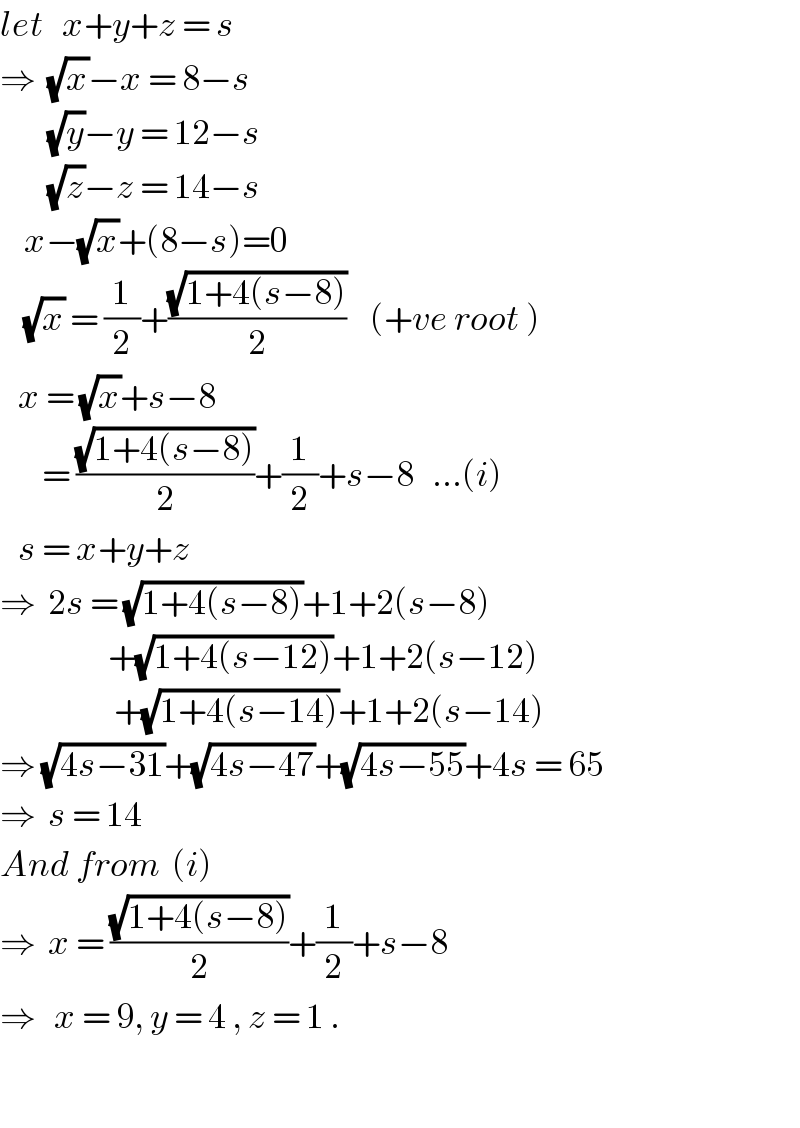
let x+y+z = s ⇒ (√x)−x = 8−s (√y)−y = 12−s (√z)−z = 14−s x−(√x)+(8−s)=0 (√x) = (1/2)+((√(1+4(s−8)))/2) (+ve root ) x = (√x)+s−8 = ((√(1+4(s−8)))/2)+(1/2)+s−8 ...(i) s = x+y+z ⇒ 2s = (√(1+4(s−8)))+1+2(s−8) +(√(1+4(s−12)))+1+2(s−12) +(√(1+4(s−14)))+1+2(s−14) ⇒ (√(4s−31))+(√(4s−47))+(√(4s−55))+4s = 65 ⇒ s = 14 And from (i) ⇒ x = ((√(1+4(s−8)))/2)+(1/2)+s−8 ⇒ x = 9, y = 4 , z = 1 .

$${let}\:\:\:{x}+{y}+{z}\:=\:{s} \\ $$$$\Rightarrow\:\:\sqrt{{x}}−{x}\:=\:\mathrm{8}−{s} \\ $$$$\:\:\:\:\:\:\:\:\sqrt{{y}}−{y}\:=\:\mathrm{12}−{s} \\ $$$$\:\:\:\:\:\:\:\:\sqrt{{z}}−{z}\:=\:\mathrm{14}−{s} \\ $$$$\:\:\:\:{x}−\sqrt{{x}}+\left(\mathrm{8}−{s}\right)=\mathrm{0} \\ $$$$\:\:\:\:\sqrt{{x}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{1}+\mathrm{4}\left({s}−\mathrm{8}\right)}}{\mathrm{2}}\:\:\:\:\left(+{ve}\:{root}\:\right) \\ $$$$\:\:\:{x}\:=\:\sqrt{{x}}+{s}−\mathrm{8} \\ $$$$\:\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{1}+\mathrm{4}\left({s}−\mathrm{8}\right)}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+{s}−\mathrm{8}\:\:\:…\left({i}\right) \\ $$$$\:\:\:{s}\:=\:{x}+{y}+{z} \\ $$$$\Rightarrow\:\:\mathrm{2}{s}\:=\:\sqrt{\mathrm{1}+\mathrm{4}\left({s}−\mathrm{8}\right)}+\mathrm{1}+\mathrm{2}\left({s}−\mathrm{8}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\sqrt{\mathrm{1}+\mathrm{4}\left({s}−\mathrm{12}\right)}+\mathrm{1}+\mathrm{2}\left({s}−\mathrm{12}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\sqrt{\mathrm{1}+\mathrm{4}\left({s}−\mathrm{14}\right)}+\mathrm{1}+\mathrm{2}\left({s}−\mathrm{14}\right) \\ $$$$\Rightarrow\:\sqrt{\mathrm{4}{s}−\mathrm{31}}+\sqrt{\mathrm{4}{s}−\mathrm{47}}+\sqrt{\mathrm{4}{s}−\mathrm{55}}+\mathrm{4}{s}\:=\:\mathrm{65} \\ $$$$\Rightarrow\:\:{s}\:=\:\mathrm{14} \\ $$$${And}\:{from}\:\:\left({i}\right) \\ $$$$\Rightarrow\:\:{x}\:=\:\frac{\sqrt{\mathrm{1}+\mathrm{4}\left({s}−\mathrm{8}\right)}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+{s}−\mathrm{8} \\ $$$$\Rightarrow\:\:\:{x}\:=\:\mathrm{9},\:{y}\:=\:\mathrm{4}\:,\:{z}\:=\:\mathrm{1}\:. \\ $$$$ \\ $$

Commented by Tawa1 last updated on 19/Dec/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply