Question Number 50754 by peter frank last updated on 19/Dec/18

Answered by tanmay.chaudhury50@gmail.com last updated on 20/Dec/18
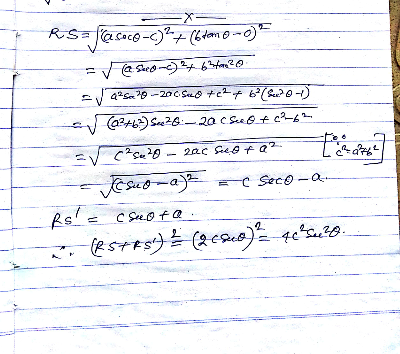
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Dec/18
![R(asecθ,btanθ) centre(0,0) S(c,0) S^′ (−c,0) c=(√(a^2 +b^2 )) tangent ((xsecθ)/a)−((ytanθ)/b)=1 distance from (0,0) is p p=∣((−1)/( (√((((secθ)/a))^2 +(−((tanθ)/b))^2 ))))∣ (1/p^2 )=((sec^2 θ)/a^2 )+((tan^2 θ)/b^2 ) LHS 4a^2 (1+(b^2 /p^2 )) =4a^2 +((4a^2 b^2 )/p^2 ) =4a^2 +4a^2 b^2 (((sec^2 θ)/a^2 )+((tan^2 θ)/b^2 )) =4a^2 +4b^2 sec^2 θ+4a^2 tan^2 θ =4a^2 (1+tan^2 θ)+4b^2 sec^2 θ =4sec^2 θ×(a^2 +b^2 ) =4c^2 sec^2 θ [since a^2 +b^2 =c^2 ] RHS (RS+RS′)^2 RS=(√((asecθ−c)^2 +(btanθ)^2 )) =(√(a^2 sec^2 θ−2acsecθ+c^2 +b^2 (sec^2 θ−1))) =(√((a^2 +b^2 )sec^2 θ−2acsecθ+c^2 −b^2 )) =(√(c^2 sec^2 θ−2acsecθ+a^2 )) =csecθ−a RS^′ =csecθ+a (RS+RS^′ )^2 =(2csecθ)^2 =4c^2 sec^2 θ proved R](https://www.tinkutara.com/question/Q50786.png)
$${R}\left({asec}\theta,{btan}\theta\right)\:\:{centre}\left(\mathrm{0},\mathrm{0}\right)\:{S}\left({c},\mathrm{0}\right)\:{S}^{'} \left(−{c},\mathrm{0}\right)\:\:{c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\: \\ $$$${tangent}\:\frac{{xsec}\theta}{{a}}−\frac{{ytan}\theta}{{b}}=\mathrm{1} \\ $$$${distance}\:{from}\:\left(\mathrm{0},\mathrm{0}\right)\:{is}\:{p} \\ $$$${p}=\mid\frac{−\mathrm{1}}{\:\sqrt{\left(\frac{{sec}\theta}{{a}}\right)^{\mathrm{2}} +\left(−\frac{{tan}\theta}{{b}}\right)^{\mathrm{2}} }}\mid \\ $$$$\frac{\mathrm{1}}{{p}^{\mathrm{2}} }=\frac{{sec}^{\mathrm{2}} \theta}{{a}^{\mathrm{2}} }+\frac{{tan}^{\mathrm{2}} \theta}{{b}^{\mathrm{2}} } \\ $$$${LHS} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} \left(\mathrm{1}+\frac{{b}^{\mathrm{2}} }{{p}^{\mathrm{2}} }\right) \\ $$$$=\mathrm{4}{a}^{\mathrm{2}} +\frac{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{p}^{\mathrm{2}} } \\ $$$$=\mathrm{4}{a}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left(\frac{{sec}^{\mathrm{2}} \theta}{{a}^{\mathrm{2}} }+\frac{{tan}^{\mathrm{2}} \theta}{{b}^{\mathrm{2}} }\right) \\ $$$$=\mathrm{4}{a}^{\mathrm{2}} +\mathrm{4}{b}^{\mathrm{2}} {sec}^{\mathrm{2}} \theta+\mathrm{4}{a}^{\mathrm{2}} {tan}^{\mathrm{2}} \theta \\ $$$$=\mathrm{4}{a}^{\mathrm{2}} \left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)+\mathrm{4}{b}^{\mathrm{2}} {sec}^{\mathrm{2}} \theta \\ $$$$=\mathrm{4}{sec}^{\mathrm{2}} \theta×\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$$$=\mathrm{4}{c}^{\mathrm{2}} {sec}^{\mathrm{2}} \theta\:\:\:\left[{since}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={c}^{\mathrm{2}} \right] \\ $$$${RHS} \\ $$$$\left({RS}+{RS}'\right)^{\mathrm{2}} \\ $$$$\:{RS}=\sqrt{\left({asec}\theta−{c}\right)^{\mathrm{2}} +\left({btan}\theta\right)^{\mathrm{2}} }\: \\ $$$$=\sqrt{{a}^{\mathrm{2}} {sec}^{\mathrm{2}} \theta−\mathrm{2}{acsec}\theta+{c}^{\mathrm{2}} +{b}^{\mathrm{2}} \left({sec}^{\mathrm{2}} \theta−\mathrm{1}\right)}\: \\ $$$$=\sqrt{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){sec}^{\mathrm{2}} \theta−\mathrm{2}{acsec}\theta+{c}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$=\sqrt{{c}^{\mathrm{2}} {sec}^{\mathrm{2}} \theta−\mathrm{2}{acsec}\theta+{a}^{\mathrm{2}} } \\ $$$$={csec}\theta−{a} \\ $$$${RS}^{'} ={csec}\theta+{a} \\ $$$$\left({RS}+{RS}^{'} \right)^{\mathrm{2}} \\ $$$$=\left(\mathrm{2}{csec}\theta\right)^{\mathrm{2}} =\mathrm{4}{c}^{\mathrm{2}} {sec}^{\mathrm{2}} \theta \\ $$$${proved} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$${R} \\ $$
Answered by ajfour last updated on 20/Dec/18
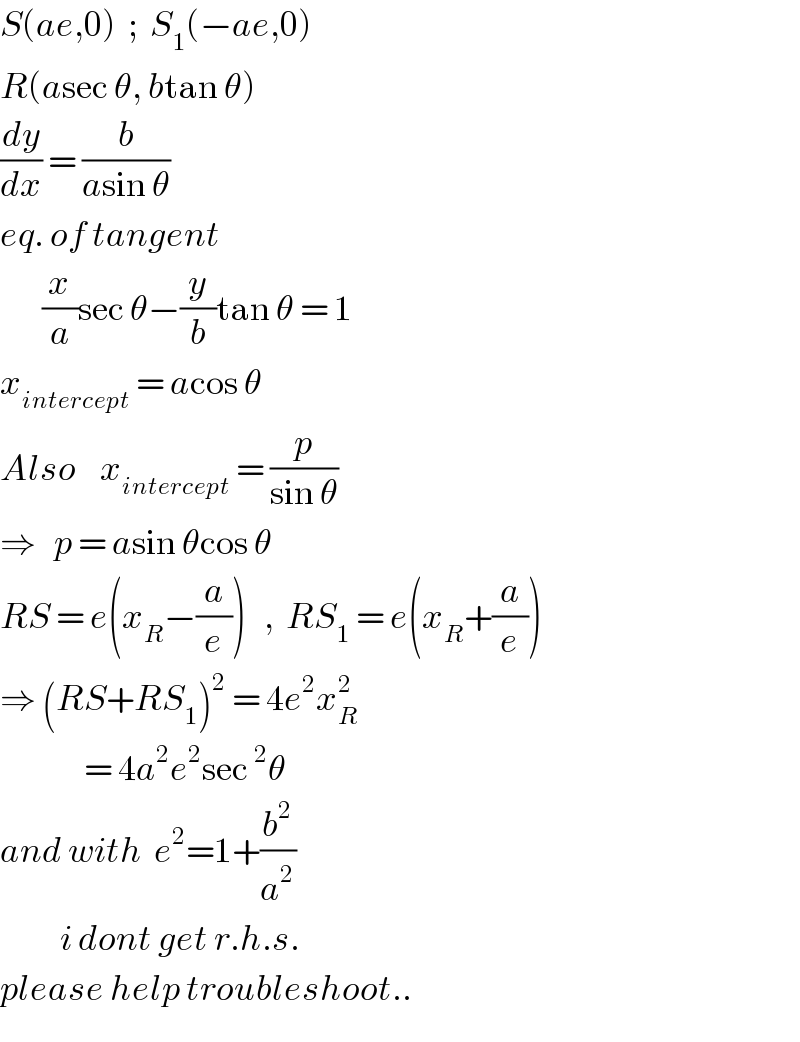
$${S}\left({ae},\mathrm{0}\right)\:\:;\:\:{S}_{\mathrm{1}} \left(−{ae},\mathrm{0}\right) \\ $$$${R}\left({a}\mathrm{sec}\:\theta,\:{b}\mathrm{tan}\:\theta\right) \\ $$$$\frac{{dy}}{{dx}}\:=\:\frac{{b}}{{a}\mathrm{sin}\:\theta} \\ $$$${eq}.\:{of}\:{tangent} \\ $$$$\:\:\:\:\:\:\:\frac{{x}}{{a}}\mathrm{sec}\:\theta−\frac{{y}}{{b}}\mathrm{tan}\:\theta\:=\:\mathrm{1} \\ $$$${x}_{{intercept}} \:=\:{a}\mathrm{cos}\:\theta \\ $$$${Also}\:\:\:\:{x}_{{intercept}} \:=\:\frac{{p}}{\mathrm{sin}\:\theta} \\ $$$$\Rightarrow\:\:\:{p}\:=\:{a}\mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$${RS}\:=\:{e}\left({x}_{{R}} −\frac{{a}}{{e}}\right)\:\:\:,\:\:{RS}_{\mathrm{1}} \:=\:{e}\left({x}_{{R}} +\frac{{a}}{{e}}\right) \\ $$$$\Rightarrow\:\left({RS}+{RS}_{\mathrm{1}} \right)^{\mathrm{2}} \:=\:\mathrm{4}{e}^{\mathrm{2}} {x}_{{R}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{4}{a}^{\mathrm{2}} {e}^{\mathrm{2}} \mathrm{sec}\:^{\mathrm{2}} \theta \\ $$$${and}\:{with}\:\:{e}^{\mathrm{2}} =\mathrm{1}+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:{i}\:{dont}\:{get}\:{r}.{h}.{s}. \\ $$$${please}\:{help}\:{troubleshoot}.. \\ $$
