Question Number 50762 by ajfour last updated on 19/Dec/18

Commented by ajfour last updated on 19/Dec/18
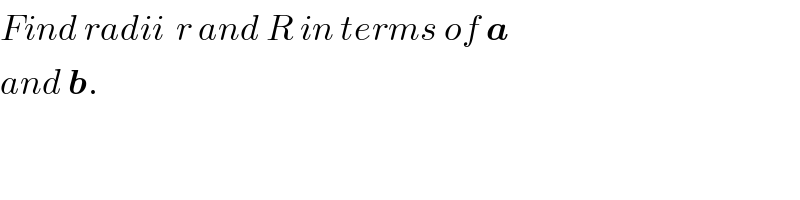
$${Find}\:{radii}\:\:{r}\:{and}\:{R}\:{in}\:{terms}\:{of}\:\boldsymbol{{a}} \\ $$$${and}\:\boldsymbol{{b}}. \\ $$
Answered by mr W last updated on 20/Dec/18
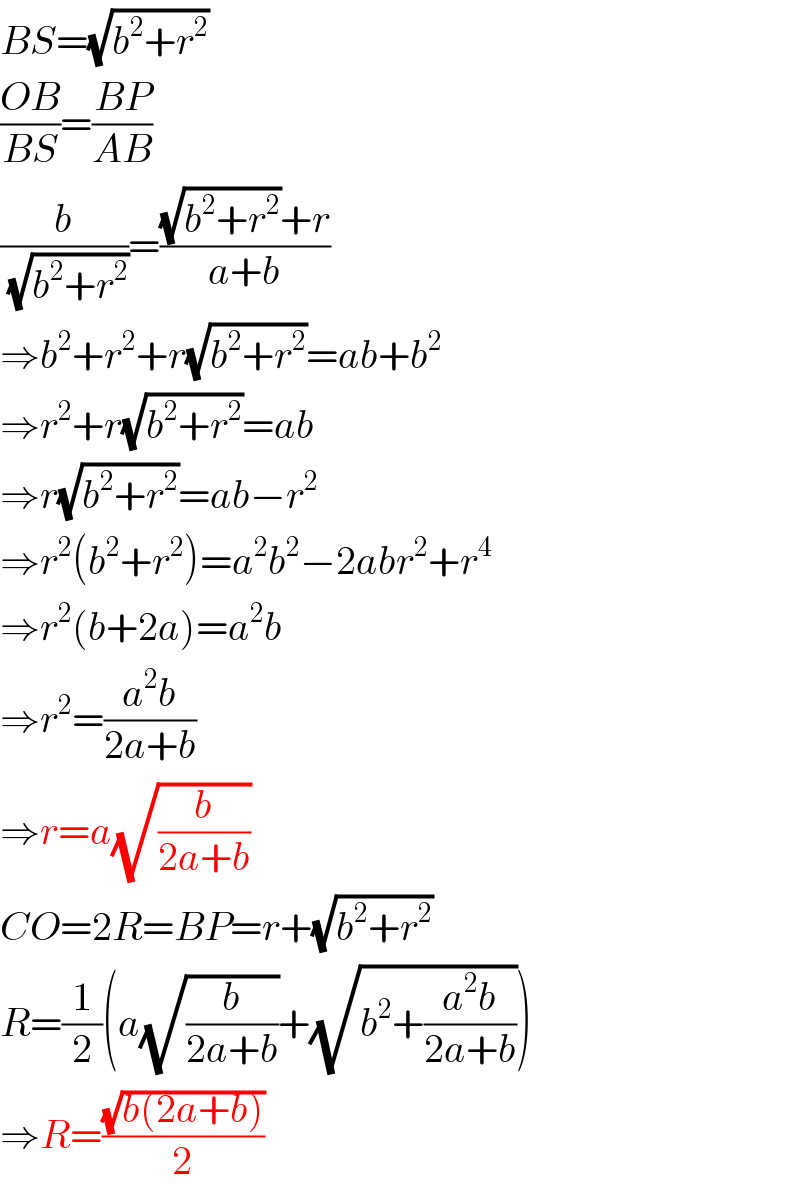
$${BS}=\sqrt{{b}^{\mathrm{2}} +{r}^{\mathrm{2}} } \\ $$$$\frac{{OB}}{{BS}}=\frac{{BP}}{{AB}} \\ $$$$\frac{{b}}{\:\sqrt{{b}^{\mathrm{2}} +{r}^{\mathrm{2}} }}=\frac{\sqrt{{b}^{\mathrm{2}} +{r}^{\mathrm{2}} }+{r}}{{a}+{b}} \\ $$$$\Rightarrow{b}^{\mathrm{2}} +{r}^{\mathrm{2}} +{r}\sqrt{{b}^{\mathrm{2}} +{r}^{\mathrm{2}} }={ab}+{b}^{\mathrm{2}} \\ $$$$\Rightarrow{r}^{\mathrm{2}} +{r}\sqrt{{b}^{\mathrm{2}} +{r}^{\mathrm{2}} }={ab} \\ $$$$\Rightarrow{r}\sqrt{{b}^{\mathrm{2}} +{r}^{\mathrm{2}} }={ab}−{r}^{\mathrm{2}} \\ $$$$\Rightarrow{r}^{\mathrm{2}} \left({b}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)={a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{2}{abr}^{\mathrm{2}} +{r}^{\mathrm{4}} \\ $$$$\Rightarrow{r}^{\mathrm{2}} \left({b}+\mathrm{2}{a}\right)={a}^{\mathrm{2}} {b} \\ $$$$\Rightarrow{r}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} {b}}{\mathrm{2}{a}+{b}} \\ $$$$\Rightarrow{r}={a}\sqrt{\frac{{b}}{\mathrm{2}{a}+{b}}} \\ $$$${CO}=\mathrm{2}{R}={BP}={r}+\sqrt{{b}^{\mathrm{2}} +{r}^{\mathrm{2}} } \\ $$$${R}=\frac{\mathrm{1}}{\mathrm{2}}\left({a}\sqrt{\frac{{b}}{\mathrm{2}{a}+{b}}}+\sqrt{{b}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} {b}}{\mathrm{2}{a}+{b}}}\right) \\ $$$$\Rightarrow{R}=\frac{\sqrt{{b}\left(\mathrm{2}{a}+{b}\right)}}{\mathrm{2}} \\ $$
Commented by ajfour last updated on 20/Dec/18
$${Thank}\:{you}\:{Sir},\:{absolutely}\:{fine}. \\ $$$$\left({source}:\:{ajfour}\right) \\ $$
