Question Number 50811 by ajfour last updated on 20/Dec/18

Commented by ajfour last updated on 20/Dec/18

$${Find}\:{distance}\:{between}\:{centres} \\ $$$${of}\:{the}\:{two}\:{equal}\:{ellipses}. \\ $$
Commented by ajfour last updated on 21/Dec/18

Answered by mr W last updated on 20/Dec/18
![y=b(√(1−((x/a))^2 )) 2∫_h ^a b(√(1−((x/a))^2 )) dx=((πab)/6) ∫_h ^a (√(1−((x/a))^2 )) d((x/a))=(π/(12)) (1/2)[((x/a))(√(1−((x/a))^2 ))+sin^(−1) ((x/a))]_h ^a =(π/(12)) (1/2)[(π/2)−((h/a))(√(1−((h/a))^2 ))−sin^(−1) ((h/a))]=(π/(12)) ((h/a))(√(1−((h/a))^2 ))+sin^(−1) ((h/a))=(π/3) ⇒(h/a)≈0.5533 distance between centers of ellipse: d=2h≈1.107a](https://www.tinkutara.com/question/Q50813.png)
$${y}={b}\sqrt{\mathrm{1}−\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{2}\int_{{h}} ^{{a}} {b}\sqrt{\mathrm{1}−\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} }\:{dx}=\frac{\pi{ab}}{\mathrm{6}} \\ $$$$\int_{{h}} ^{{a}} \sqrt{\mathrm{1}−\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} }\:{d}\left(\frac{{x}}{{a}}\right)=\frac{\pi}{\mathrm{12}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\frac{{x}}{{a}}\right)\sqrt{\mathrm{1}−\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} }+\mathrm{sin}^{−\mathrm{1}} \left(\frac{{x}}{{a}}\right)\right]_{{h}} ^{{a}} =\frac{\pi}{\mathrm{12}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\pi}{\mathrm{2}}−\left(\frac{{h}}{{a}}\right)\sqrt{\mathrm{1}−\left(\frac{{h}}{{a}}\right)^{\mathrm{2}} }−\mathrm{sin}^{−\mathrm{1}} \left(\frac{{h}}{{a}}\right)\right]=\frac{\pi}{\mathrm{12}} \\ $$$$\left(\frac{{h}}{{a}}\right)\sqrt{\mathrm{1}−\left(\frac{{h}}{{a}}\right)^{\mathrm{2}} }+\mathrm{sin}^{−\mathrm{1}} \left(\frac{{h}}{{a}}\right)=\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow\frac{{h}}{{a}}\approx\mathrm{0}.\mathrm{5533} \\ $$$${distance}\:{between}\:{centers}\:{of}\:{ellipse}: \\ $$$${d}=\mathrm{2}{h}\approx\mathrm{1}.\mathrm{107}{a} \\ $$
Commented by ajfour last updated on 20/Dec/18
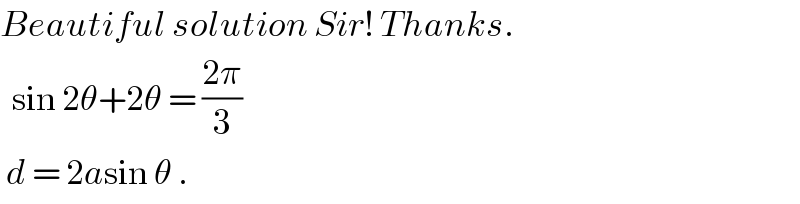
$${Beautiful}\:{solution}\:{Sir}!\:{Thanks}. \\ $$$$\:\:\mathrm{sin}\:\mathrm{2}\theta+\mathrm{2}\theta\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\:{d}\:=\:\mathrm{2}{a}\mathrm{sin}\:\theta\:. \\ $$
