Question Number 50829 by Raj Singh last updated on 21/Dec/18
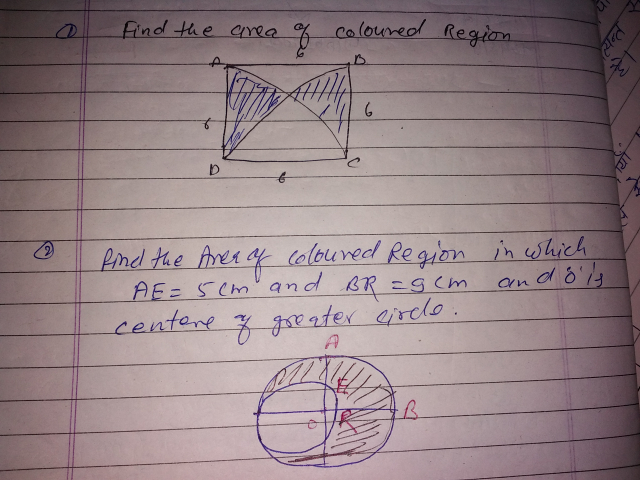
Commented by Raj Singh last updated on 21/Dec/18

$${this}\:{is}\:{class}\:\mathrm{10}\:{problem}\:{so}\:{solve} \\ $$$${by}\:{general}\:{method} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Dec/18
![area of square=a^2 area of ADCA sector=(1/4)×πa^2 DC=x axis DA=y axis sector ADCA part of circle x^2 +y^2 =a^2 sector DCBD part of circle (x−a)^2 +y^2 =a^2 solving x^2 =(x−a)^2 x^2 =x^2 −2xa+a^2 so 2xa=a^2 x=(a/2) area of big white portion=W ∫_0 ^(a/2) (√(a^2 −(x−a)^2 )) dx+∫_(a/2) ^a (√(a^2 −x^2 )) dx=W so required shaded area=2((1/4)πa^2 −W) formula ∫(√(A^2 −X^2 )) dX=(X/2)(√(A^2 −X^2 )) +(A^2 /2)sin^(−1) ((X/A)) I_1 =∣((x−a)/2)(√(a^2 −(x−a)^2 )) +(a^2 /2)sin^(−1) (((x−a)/a))∣_0 ^(a/2) ={(((−a)/4)×a((√3)/2))+(a^2 /2)sin^(−1) (((−1)/2))−(a^2 /2)sin^(−1) (−1)} =((−(√3))/8)a^2 −(a^2 /2)((π/6))+(a^2 /2)×(π/2) I_2 =∣(x/2)(√(a^2 −x^2 )) +(a^2 /2)sin^(−1) ((x/a))∣_(a/2) ^a =(a/2)×0+(a^2 /2)×(π/2)−(a/4)×((a(√3))/2)−(a^2 /2)×(π/6) =((πa^2 )/4)−((a^2 (√3))/8)−((πa^2 )/(12)) W=2(((πa^2 )/4)−((√3)/8)a^2 −((πa^2 )/(12)))=((πa^2 )/2)−(((√3) a^2 )/4)−((πa^2 )/6) so required area 2[((πa^2 )/4)−((πa^2 )/2)+(((√3) a^2 )/4)+((πa^2 )/6)] =2[((3πa^2 −6πa^2 +3(√3) a^2 +2πa^2 )/(12))] =(1/6)[3(√3) a^2 −πa^2 ] pls check](https://www.tinkutara.com/question/Q50830.png)
$${area}\:{of}\:{square}={a}^{\mathrm{2}} \\ $$$${area}\:{of}\:{ADCA}\:{sector}=\frac{\mathrm{1}}{\mathrm{4}}×\pi{a}^{\mathrm{2}} \\ $$$${DC}={x}\:{axis}\:\:\:\:{DA}={y}\:{axis} \\ $$$${sector}\:{ADCA}\:{part}\:{of}\:{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$${sector}\:{DCBD}\:{part}\:{of}\:{circle}\:\left({x}−{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$${solving} \\ $$$${x}^{\mathrm{2}} =\left({x}−{a}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} ={x}^{\mathrm{2}} −\mathrm{2}{xa}+{a}^{\mathrm{2}} \:\:\:{so}\:\mathrm{2}{xa}={a}^{\mathrm{2}} \:\:\:{x}=\frac{{a}}{\mathrm{2}} \\ $$$${area}\:{of}\:{big}\:{white}\:{portion}=\boldsymbol{{W}} \\ $$$$\int_{\mathrm{0}} ^{\frac{{a}}{\mathrm{2}}} \sqrt{{a}^{\mathrm{2}} −\left({x}−{a}\right)^{\mathrm{2}} }\:{dx}+\int_{\frac{{a}}{\mathrm{2}}} ^{{a}} \sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:{dx}=\boldsymbol{{W}} \\ $$$${so}\:{required}\:{shaded}\:{area}=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{4}}\pi{a}^{\mathrm{2}} −\boldsymbol{{W}}\right) \\ $$$${formula}\:\int\sqrt{{A}^{\mathrm{2}} −{X}^{\mathrm{2}} }\:{dX}=\frac{{X}}{\mathrm{2}}\sqrt{{A}^{\mathrm{2}} −{X}^{\mathrm{2}} }\:+\frac{{A}^{\mathrm{2}} }{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{{X}}{{A}}\right) \\ $$$${I}_{\mathrm{1}} =\mid\frac{{x}−{a}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −\left({x}−{a}\right)^{\mathrm{2}} }\:+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{{x}−{a}}{{a}}\right)\mid_{\mathrm{0}} ^{\frac{{a}}{\mathrm{2}}} \\ $$$$=\left\{\left(\frac{−{a}}{\mathrm{4}}×{a}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\mathrm{2}}\right)−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{sin}^{−\mathrm{1}} \left(−\mathrm{1}\right)\right\} \\ $$$$=\frac{−\sqrt{\mathrm{3}}}{\mathrm{8}}{a}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{6}}\right)+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}×\frac{\pi}{\mathrm{2}} \\ $$$${I}_{\mathrm{2}} =\mid\frac{{x}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{{x}}{{a}}\right)\mid_{\frac{{a}}{\mathrm{2}}} ^{{a}} \\ $$$$=\frac{{a}}{\mathrm{2}}×\mathrm{0}+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}×\frac{\pi}{\mathrm{2}}−\frac{{a}}{\mathrm{4}}×\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}×\frac{\pi}{\mathrm{6}} \\ $$$$=\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}}−\frac{{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{8}}−\frac{\pi{a}^{\mathrm{2}} }{\mathrm{12}} \\ $$$${W}=\mathrm{2}\left(\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{8}}{a}^{\mathrm{2}} −\frac{\pi{a}^{\mathrm{2}} }{\mathrm{12}}\right)=\frac{\pi{a}^{\mathrm{2}} }{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}\:{a}^{\mathrm{2}} }{\mathrm{4}}−\frac{\pi{a}^{\mathrm{2}} }{\mathrm{6}} \\ $$$${so}\:{required}\:{area} \\ $$$$\mathrm{2}\left[\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}}−\frac{\pi{a}^{\mathrm{2}} }{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}\:{a}^{\mathrm{2}} }{\mathrm{4}}+\frac{\pi{a}^{\mathrm{2}} }{\mathrm{6}}\right] \\ $$$$=\mathrm{2}\left[\frac{\mathrm{3}\pi{a}^{\mathrm{2}} −\mathrm{6}\pi{a}^{\mathrm{2}} +\mathrm{3}\sqrt{\mathrm{3}}\:{a}^{\mathrm{2}} +\mathrm{2}\pi{a}^{\mathrm{2}} }{\mathrm{12}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left[\mathrm{3}\sqrt{\mathrm{3}}\:{a}^{\mathrm{2}} −\pi{a}^{\mathrm{2}} \right] \\ $$$${pls}\:{check} \\ $$$$ \\ $$
Answered by mr W last updated on 21/Dec/18
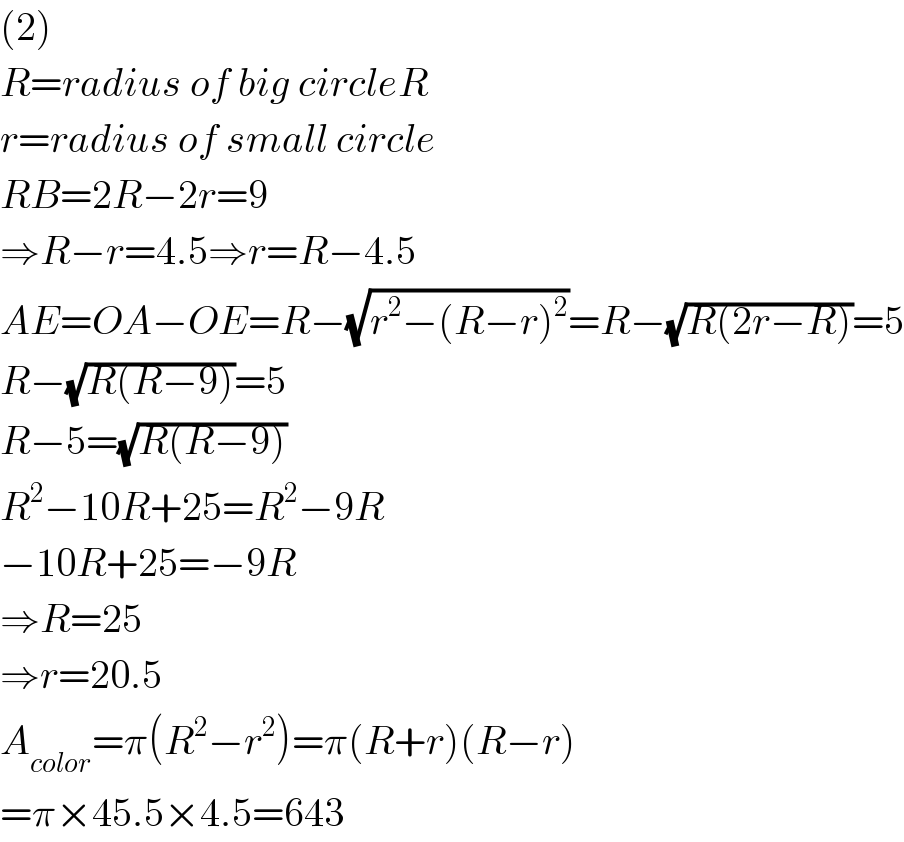
$$\left(\mathrm{2}\right) \\ $$$${R}={radius}\:{of}\:{big}\:{circleR} \\ $$$${r}={radius}\:{of}\:{small}\:{circle} \\ $$$${RB}=\mathrm{2}{R}−\mathrm{2}{r}=\mathrm{9} \\ $$$$\Rightarrow{R}−{r}=\mathrm{4}.\mathrm{5}\Rightarrow{r}={R}−\mathrm{4}.\mathrm{5} \\ $$$${AE}={OA}−{OE}={R}−\sqrt{{r}^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} }={R}−\sqrt{{R}\left(\mathrm{2}{r}−{R}\right)}=\mathrm{5} \\ $$$${R}−\sqrt{{R}\left({R}−\mathrm{9}\right)}=\mathrm{5} \\ $$$${R}−\mathrm{5}=\sqrt{{R}\left({R}−\mathrm{9}\right)} \\ $$$${R}^{\mathrm{2}} −\mathrm{10}{R}+\mathrm{25}={R}^{\mathrm{2}} −\mathrm{9}{R} \\ $$$$−\mathrm{10}{R}+\mathrm{25}=−\mathrm{9}{R} \\ $$$$\Rightarrow{R}=\mathrm{25} \\ $$$$\Rightarrow{r}=\mathrm{20}.\mathrm{5} \\ $$$${A}_{{color}} =\pi\left({R}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)=\pi\left({R}+{r}\right)\left({R}−{r}\right) \\ $$$$=\pi×\mathrm{45}.\mathrm{5}×\mathrm{4}.\mathrm{5}=\mathrm{643} \\ $$
