Question Number 50834 by Tinkutara last updated on 21/Dec/18

Commented by ajfour last updated on 21/Dec/18
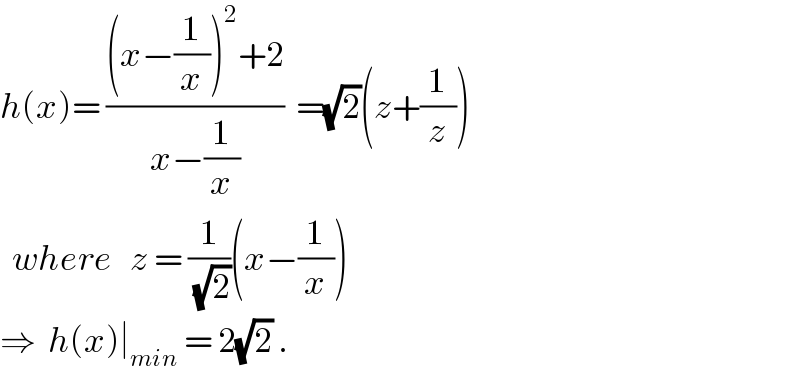
$${h}\left({x}\right)=\:\frac{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}}{{x}−\frac{\mathrm{1}}{{x}}}\:\:=\sqrt{\mathrm{2}}\left({z}+\frac{\mathrm{1}}{{z}}\right) \\ $$$$\:\:{where}\:\:\:{z}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left({x}−\frac{\mathrm{1}}{{x}}\right) \\ $$$$\Rightarrow\:\:{h}\left({x}\right)\mid_{{min}} \:=\:\mathrm{2}\sqrt{\mathrm{2}}\:. \\ $$
Commented by Tawa1 last updated on 21/Dec/18
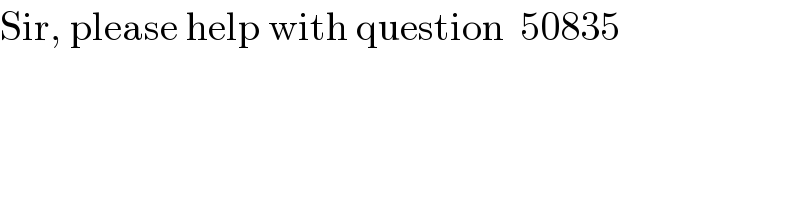
$$\mathrm{Sir},\:\mathrm{please}\:\mathrm{help}\:\mathrm{with}\:\mathrm{question}\:\:\mathrm{50835} \\ $$
Commented by ajfour last updated on 21/Dec/18

$${when}\:{z}\:{is}\:{negative},\:{i}\:{think}\:{local} \\ $$$${maximum}\:{is}\:{there}. \\ $$
Commented by Tinkutara last updated on 22/Dec/18
Thanks Sir!
