Question Number 50963 by ajfour last updated on 22/Dec/18

Commented by ajfour last updated on 22/Dec/18
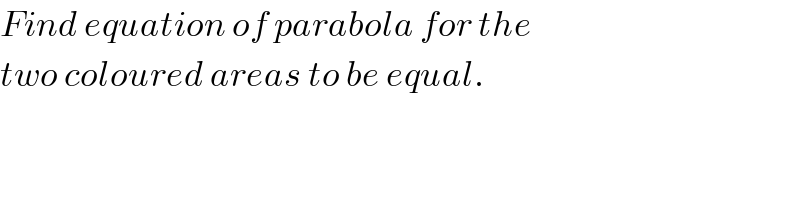
$${Find}\:{equation}\:{of}\:{parabola}\:{for}\:{the} \\ $$$${two}\:{coloured}\:{areas}\:{to}\:{be}\:{equal}. \\ $$
Answered by mr W last updated on 23/Dec/18
![parabola: y=cx^2 line: (x/a)+(y/b)=1 (x/a)+((cx^2 )/b)=1 ⇒acx^2 +bx−ab=0 ⇒x=h=((−b+(√(b^2 +4a^2 bc)))/(2ac)) A_(green) =∫_0 ^h (b−((bx)/a)−cx^2 )dx=((ab)/4) bh−((bh^2 )/(2a))−((ch^3 )/3)=((ab)/4) h[b−h((b/(2a))+((ch)/3))]=((ab)/4) ⇒solve for c.... example: a=4,b=3⇒c=0.6211⇒y=0.6211x^2](https://www.tinkutara.com/question/Q50981.png)
$${parabola}:\:{y}={cx}^{\mathrm{2}} \\ $$$${line}:\:\frac{{x}}{{a}}+\frac{{y}}{{b}}=\mathrm{1} \\ $$$$\frac{{x}}{{a}}+\frac{{cx}^{\mathrm{2}} }{{b}}=\mathrm{1} \\ $$$$\Rightarrow{acx}^{\mathrm{2}} +{bx}−{ab}=\mathrm{0} \\ $$$$\Rightarrow{x}={h}=\frac{−{b}+\sqrt{{b}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} {bc}}}{\mathrm{2}{ac}} \\ $$$${A}_{{green}} =\int_{\mathrm{0}} ^{{h}} \left({b}−\frac{{bx}}{{a}}−{cx}^{\mathrm{2}} \right){dx}=\frac{{ab}}{\mathrm{4}} \\ $$$${bh}−\frac{{bh}^{\mathrm{2}} }{\mathrm{2}{a}}−\frac{{ch}^{\mathrm{3}} }{\mathrm{3}}=\frac{{ab}}{\mathrm{4}} \\ $$$${h}\left[{b}−{h}\left(\frac{{b}}{\mathrm{2}{a}}+\frac{{ch}}{\mathrm{3}}\right)\right]=\frac{{ab}}{\mathrm{4}} \\ $$$$\Rightarrow{solve}\:{for}\:{c}…. \\ $$$$ \\ $$$${example}: \\ $$$${a}=\mathrm{4},{b}=\mathrm{3}\Rightarrow{c}=\mathrm{0}.\mathrm{6211}\Rightarrow{y}=\mathrm{0}.\mathrm{6211}{x}^{\mathrm{2}} \\ $$
Commented by ajfour last updated on 23/Dec/18

$${Thank}\:{you}\:{Sir}. \\ $$
Answered by ajfour last updated on 23/Dec/18
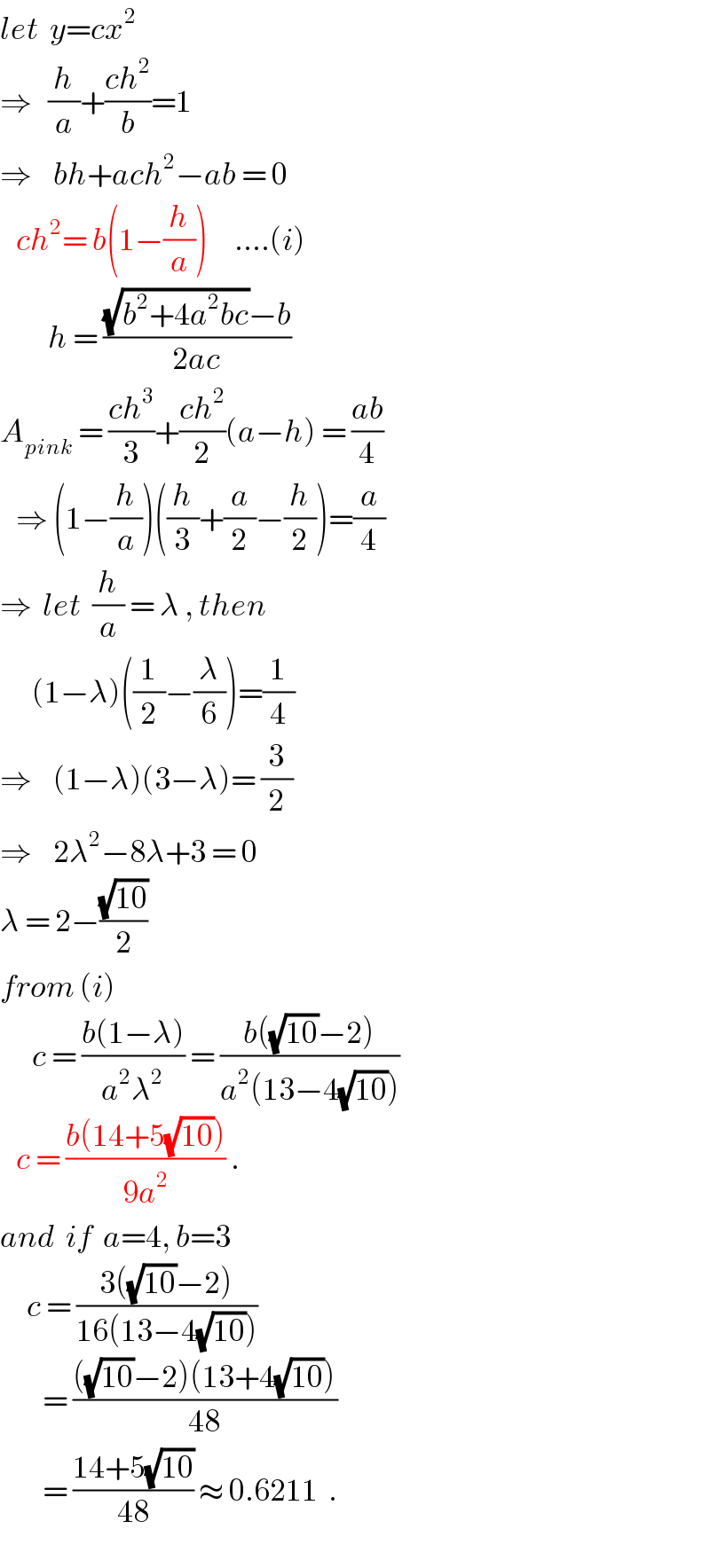
$${let}\:\:{y}={cx}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\frac{{h}}{{a}}+\frac{{ch}^{\mathrm{2}} }{{b}}=\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:{bh}+{ach}^{\mathrm{2}} −{ab}\:=\:\mathrm{0} \\ $$$$\:\:\:{ch}^{\mathrm{2}} =\:{b}\left(\mathrm{1}−\frac{{h}}{{a}}\right)\:\:\:\:\:….\left({i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:{h}\:=\:\frac{\sqrt{{b}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} {bc}}−{b}}{\mathrm{2}{ac}} \\ $$$${A}_{{pink}} \:=\:\frac{{ch}^{\mathrm{3}} }{\mathrm{3}}+\frac{{ch}^{\mathrm{2}} }{\mathrm{2}}\left({a}−{h}\right)\:=\:\frac{{ab}}{\mathrm{4}} \\ $$$$\:\:\:\Rightarrow\:\left(\mathrm{1}−\frac{{h}}{{a}}\right)\left(\frac{{h}}{\mathrm{3}}+\frac{{a}}{\mathrm{2}}−\frac{{h}}{\mathrm{2}}\right)=\frac{{a}}{\mathrm{4}} \\ $$$$\Rightarrow\:\:{let}\:\:\frac{{h}}{{a}}\:=\:\lambda\:,\:{then} \\ $$$$\:\:\:\:\:\:\left(\mathrm{1}−\lambda\right)\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\lambda}{\mathrm{6}}\right)=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\:\:\:\:\left(\mathrm{1}−\lambda\right)\left(\mathrm{3}−\lambda\right)=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:\mathrm{2}\lambda^{\mathrm{2}} −\mathrm{8}\lambda+\mathrm{3}\:=\:\mathrm{0} \\ $$$$\lambda\:=\:\mathrm{2}−\frac{\sqrt{\mathrm{10}}}{\mathrm{2}} \\ $$$${from}\:\left({i}\right) \\ $$$$\:\:\:\:\:\:{c}\:=\:\frac{{b}\left(\mathrm{1}−\lambda\right)}{{a}^{\mathrm{2}} \lambda^{\mathrm{2}} }\:=\:\frac{{b}\left(\sqrt{\mathrm{10}}−\mathrm{2}\right)}{{a}^{\mathrm{2}} \left(\mathrm{13}−\mathrm{4}\sqrt{\mathrm{10}}\right)}\:\: \\ $$$$\:\:\:{c}\:=\:\frac{{b}\left(\mathrm{14}+\mathrm{5}\sqrt{\mathrm{10}}\right)}{\mathrm{9}{a}^{\mathrm{2}} }\:. \\ $$$${and}\:\:{if}\:\:{a}=\mathrm{4},\:{b}=\mathrm{3} \\ $$$$\:\:\:\:\:{c}\:=\:\frac{\mathrm{3}\left(\sqrt{\mathrm{10}}−\mathrm{2}\right)}{\mathrm{16}\left(\mathrm{13}−\mathrm{4}\sqrt{\mathrm{10}}\right)}\: \\ $$$$\:\:\:\:\:\:\:\:=\:\frac{\left(\sqrt{\mathrm{10}}−\mathrm{2}\right)\left(\mathrm{13}+\mathrm{4}\sqrt{\mathrm{10}}\right)}{\mathrm{48}} \\ $$$$\:\:\:\:\:\:\:\:=\:\frac{\mathrm{14}+\mathrm{5}\sqrt{\mathrm{10}}}{\mathrm{48}}\:\approx\:\mathrm{0}.\mathrm{6211}\:\:. \\ $$
Commented by mr W last updated on 23/Dec/18
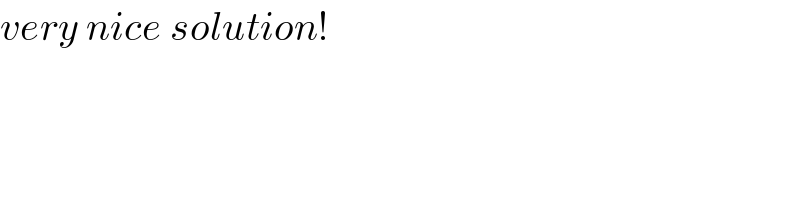
$${very}\:{nice}\:{solution}! \\ $$
