Question Number 50967 by ajfour last updated on 22/Dec/18

Commented by ajfour last updated on 22/Dec/18

$${String}\:{is}\:{wrapped}\:{over}\:{cylinder}, \\ $$$${find}\:\boldsymbol{{l}}\:{for}\:{equilibrium}. \\ $$
Answered by ajfour last updated on 23/Dec/18
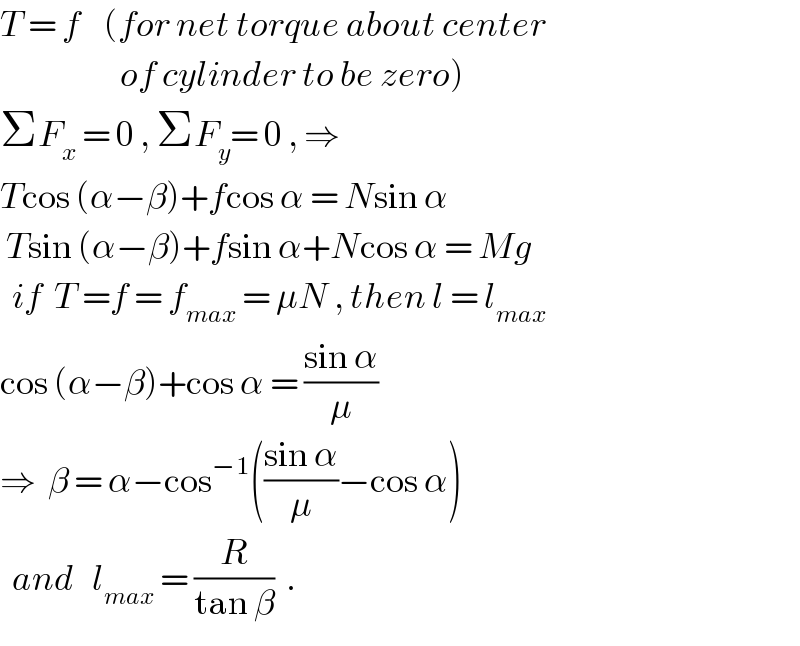
$${T}\:=\:{f}\:\:\:\:\left({for}\:{net}\:{torque}\:{about}\:{center}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{of}\:{cylinder}\:{to}\:{be}\:{zero}\right) \\ $$$$\Sigma{F}_{{x}} \:=\:\mathrm{0}\:,\:\Sigma{F}_{{y}} =\:\mathrm{0}\:,\:\Rightarrow \\ $$$${T}\mathrm{cos}\:\left(\alpha−\beta\right)+{f}\mathrm{cos}\:\alpha\:=\:{N}\mathrm{sin}\:\alpha \\ $$$$\:{T}\mathrm{sin}\:\left(\alpha−\beta\right)+{f}\mathrm{sin}\:\alpha+{N}\mathrm{cos}\:\alpha\:=\:{Mg} \\ $$$$\:\:{if}\:\:{T}\:={f}\:=\:{f}_{{max}} \:=\:\mu{N}\:,\:{then}\:{l}\:=\:{l}_{{max}} \\ $$$$\mathrm{cos}\:\left(\alpha−\beta\right)+\mathrm{cos}\:\alpha\:=\:\frac{\mathrm{sin}\:\alpha}{\mu} \\ $$$$\Rightarrow\:\:\beta\:=\:\alpha−\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:\alpha}{\mu}−\mathrm{cos}\:\alpha\right) \\ $$$$\:\:{and}\:\:\:{l}_{{max}} \:=\:\frac{{R}}{\mathrm{tan}\:\beta}\:\:. \\ $$
Commented by ajfour last updated on 23/Dec/18
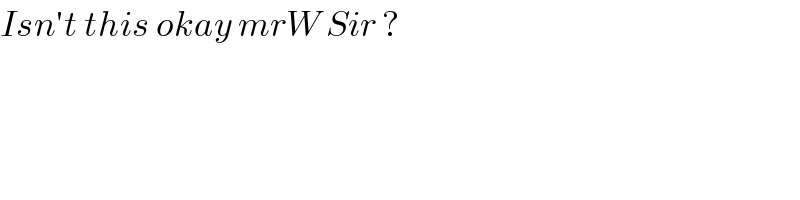
$${Isn}'{t}\:{this}\:{okay}\:{mrW}\:{Sir}\:? \\ $$
Commented by mr W last updated on 23/Dec/18

$${very}\:{fine}\:{sir}! \\ $$
