Question Number 51095 by Tinkutara last updated on 23/Dec/18
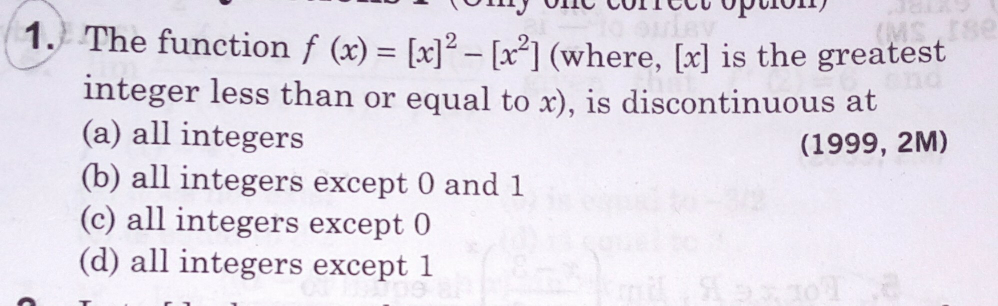
Commented by prakash jain last updated on 25/Dec/18
![lim_(x→0^+ ) [x]^2 −[x^2 ]=0 lim_(x→0^− ) [x]^2 −[x^2 ] =lim_(h→0^+ ) [−h]^2 −[(−h)^2 ] =lim_(h→0^+ ) [−h]^2 −[h^2 ]=−1−0=−1 LHL≠RHL](https://www.tinkutara.com/question/Q51225.png)
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left[{x}\right]^{\mathrm{2}} −\left[{x}^{\mathrm{2}} \right]=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\left[{x}\right]^{\mathrm{2}} −\left[{x}^{\mathrm{2}} \right] \\ $$$$=\underset{{h}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left[−{h}\right]^{\mathrm{2}} −\left[\left(−{h}\right)^{\mathrm{2}} \right] \\ $$$$=\underset{{h}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left[−{h}\right]^{\mathrm{2}} −\left[{h}^{\mathrm{2}} \right]=−\mathrm{1}−\mathrm{0}=−\mathrm{1} \\ $$$$\mathrm{LHL}\neq\mathrm{RHL} \\ $$
Commented by Tinkutara last updated on 25/Dec/18
And at 1?
Commented by prakash jain last updated on 25/Dec/18
$$\mathrm{You}\:\mathrm{can}\:\mathrm{use}\:\mathrm{the}\:\mathrm{same}\:\mathrm{logic}\:\mathrm{at}\:\mathrm{1}. \\ $$
Commented by prakash jain last updated on 25/Dec/18
![lim_(x→1^+ ) [x]^2 −[x^2 ]=1^2 −1^2 =0 lim_(x→1^− ) [x]^2 −[x^2 ]= lim_(h→0) [(1−h)]^2 −[(1−h)^2 ] =(0)^2 −(0)=0 [(1−h)^2 <1] LHL=RHL=value of function](https://www.tinkutara.com/question/Q51256.png)
$$\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\left[{x}\right]^{\mathrm{2}} −\left[{x}^{\mathrm{2}} \right]=\mathrm{1}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} =\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\left[{x}\right]^{\mathrm{2}} −\left[{x}^{\mathrm{2}} \right]= \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\mathrm{1}−{h}\right)\right]^{\mathrm{2}} −\left[\left(\mathrm{1}−{h}\right)^{\mathrm{2}} \right] \\ $$$$=\left(\mathrm{0}\right)^{\mathrm{2}} −\left(\mathrm{0}\right)=\mathrm{0}\:\left[\left(\mathrm{1}−{h}\right)^{\mathrm{2}} <\mathrm{1}\right] \\ $$$$\mathrm{LHL}=\mathrm{RHL}={value}\:{of}\:{function} \\ $$
Commented by Tinkutara last updated on 25/Dec/18
Thank you very much Sir! I got the answer. ��������
