Menu Close

Question-51134

Tinku Tara 0 Comments
Pin




Question Number 51134 by ajfour last updated on 24/Dec/18
Commented by ajfour last updated on 24/Dec/18
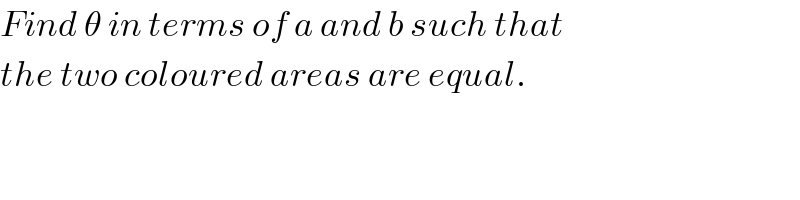
Find θ in terms of a and b such that the two coloured areas are equal.
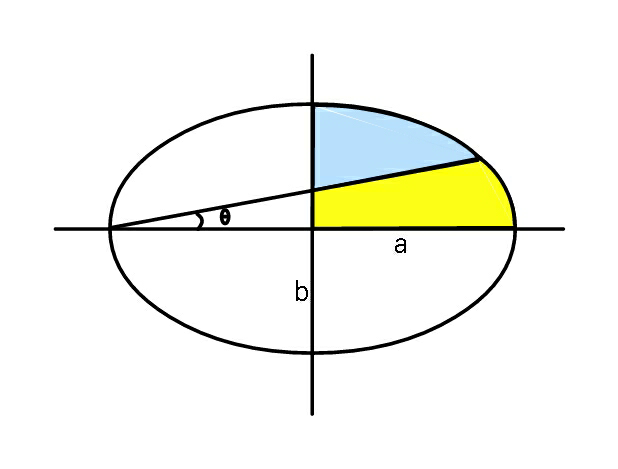
$${Find}\:\theta\:{in}\:{terms}\:{of}\:{a}\:{and}\:{b}\:{such}\:{that} \\ $$$${the}\:{two}\:{coloured}\:{areas}\:{are}\:{equal}. \\ $$
Answered by mr W last updated on 24/Dec/18
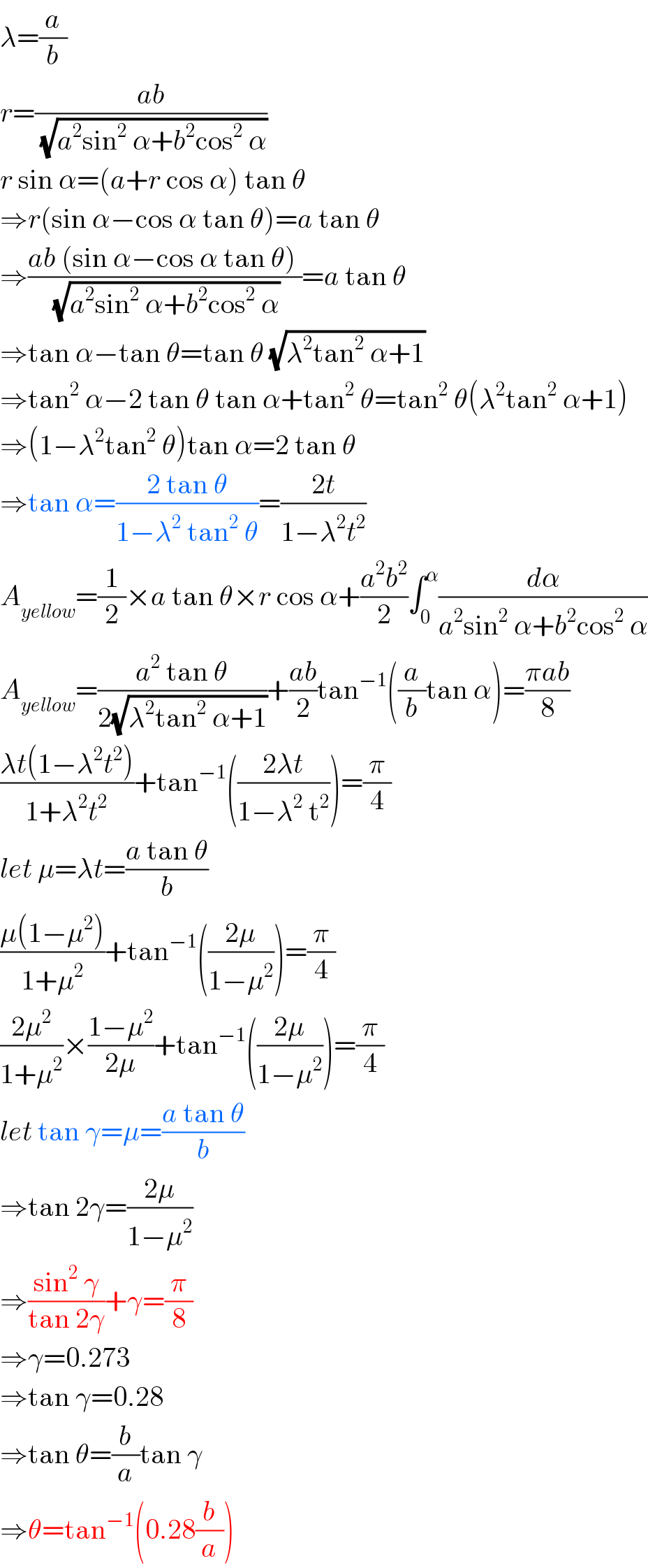
λ=(a/b) r=((ab)/( (√(a^2 sin^2 α+b^2 cos^2 α)))) r sin α=(a+r cos α) tan θ ⇒r(sin α−cos α tan θ)=a tan θ ⇒((ab (sin α−cos α tan θ) )/( (√(a^2 sin^2 α+b^2 cos^2 α))))=a tan θ ⇒tan α−tan θ=tan θ (√(λ^2 tan^2 α+1)) ⇒tan^2 α−2 tan θ tan α+tan^2 θ=tan^2 θ(λ^2 tan^2 α+1) ⇒(1−λ^2 tan^2 θ)tan α=2 tan θ ⇒tan α=((2 tan θ)/(1−λ^2 tan^2 θ))=((2t)/(1−λ^2 t^2 )) A_(yellow) =(1/2)×a tan θ×r cos α+((a^2 b^2 )/2)∫_0 ^α (dα/(a^2 sin^2 α+b^2 cos^2 α)) A_(yellow) =((a^2 tan θ)/(2(√(λ^2 tan^2 α+1))))+((ab)/2)tan^(−1) ((a/b)tan α)=((πab)/8) ((λt(1−λ^2 t^2 ))/(1+λ^2 t^2 ))+tan^(−1) (((2λt)/(1−λ^2 t^2 )))=(π/4) let μ=λt=((a tan θ)/b) ((μ(1−μ^2 ))/(1+μ^2 ))+tan^(−1) (((2μ)/(1−μ^2 )))=(π/4) ((2μ^2 )/(1+μ^2 ))×((1−μ^2 )/(2μ))+tan^(−1) (((2μ)/(1−μ^2 )))=(π/4) let tan γ=μ=((a tan θ)/b) ⇒tan 2γ=((2μ)/(1−μ^2 )) ⇒((sin^2 γ)/(tan 2γ))+γ=(π/8) ⇒γ=0.273 ⇒tan γ=0.28 ⇒tan θ=(b/a)tan γ ⇒θ=tan^(−1) (0.28(b/a))
$$\lambda=\frac{{a}}{{b}} \\ $$$${r}=\frac{{ab}}{\:\sqrt{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\alpha+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha}} \\ $$$${r}\:\mathrm{sin}\:\alpha=\left({a}+{r}\:\mathrm{cos}\:\alpha\right)\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow{r}\left(\mathrm{sin}\:\alpha−\mathrm{cos}\:\alpha\:\mathrm{tan}\:\theta\right)={a}\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow\frac{{ab}\:\left(\mathrm{sin}\:\alpha−\mathrm{cos}\:\alpha\:\mathrm{tan}\:\theta\right)\:}{\:\sqrt{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\alpha+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha}}={a}\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow\mathrm{tan}\:\alpha−\mathrm{tan}\:\theta=\mathrm{tan}\:\theta\:\sqrt{\lambda^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\alpha+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{tan}^{\mathrm{2}} \:\alpha−\mathrm{2}\:\mathrm{tan}\:\theta\:\mathrm{tan}\:\alpha+\mathrm{tan}^{\mathrm{2}} \:\theta=\mathrm{tan}^{\mathrm{2}} \:\theta\left(\lambda^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\alpha+\mathrm{1}\right) \\ $$$$\Rightarrow\left(\mathrm{1}−\lambda^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta\right)\mathrm{tan}\:\alpha=\mathrm{2}\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{2}\:\mathrm{tan}\:\theta}{\mathrm{1}−\lambda^{\mathrm{2}} \:\mathrm{tan}^{\mathrm{2}} \:\theta}=\frac{\mathrm{2}{t}}{\mathrm{1}−\lambda^{\mathrm{2}} {t}^{\mathrm{2}} } \\ $$$${A}_{{yellow}} =\frac{\mathrm{1}}{\mathrm{2}}×{a}\:\mathrm{tan}\:\theta×{r}\:\mathrm{cos}\:\alpha+\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{\mathrm{2}}\int_{\mathrm{0}} ^{\alpha} \frac{{d}\alpha}{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\alpha+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha} \\ $$$${A}_{{yellow}} =\frac{{a}^{\mathrm{2}} \:\mathrm{tan}\:\theta}{\mathrm{2}\sqrt{\lambda^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\alpha+\mathrm{1}}}+\frac{{ab}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}}{{b}}\mathrm{tan}\:\alpha\right)=\frac{\pi{ab}}{\mathrm{8}} \\ $$$$\frac{\lambda{t}\left(\mathrm{1}−\lambda^{\mathrm{2}} {t}^{\mathrm{2}} \right)}{\mathrm{1}+\lambda^{\mathrm{2}} {t}^{\mathrm{2}} }+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}\lambda{t}}{\mathrm{1}−\lambda^{\mathrm{2}} \:\mathrm{t}^{\mathrm{2}} }\right)=\frac{\pi}{\mathrm{4}} \\ $$$${let}\:\mu=\lambda{t}=\frac{{a}\:\mathrm{tan}\:\theta}{{b}} \\ $$$$\frac{\mu\left(\mathrm{1}−\mu^{\mathrm{2}} \right)}{\mathrm{1}+\mu^{\mathrm{2}} }+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}\mu}{\mathrm{1}−\mu^{\mathrm{2}} }\right)=\frac{\pi}{\mathrm{4}} \\ $$$$\frac{\mathrm{2}\mu^{\mathrm{2}} }{\mathrm{1}+\mu^{\mathrm{2}} }×\frac{\mathrm{1}−\mu^{\mathrm{2}} }{\mathrm{2}\mu}+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}\mu}{\mathrm{1}−\mu^{\mathrm{2}} }\right)=\frac{\pi}{\mathrm{4}} \\ $$$${let}\:\mathrm{tan}\:\gamma=\mu=\frac{{a}\:\mathrm{tan}\:\theta}{{b}} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{2}\gamma=\frac{\mathrm{2}\mu}{\mathrm{1}−\mu^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{sin}^{\mathrm{2}} \:\gamma}{\mathrm{tan}\:\mathrm{2}\gamma}+\gamma=\frac{\pi}{\mathrm{8}} \\ $$$$\Rightarrow\gamma=\mathrm{0}.\mathrm{273} \\ $$$$\Rightarrow\mathrm{tan}\:\gamma=\mathrm{0}.\mathrm{28} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{{b}}{{a}}\mathrm{tan}\:\gamma \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{0}.\mathrm{28}\frac{{b}}{{a}}\right) \\ $$
Commented by mr W last updated on 24/Dec/18
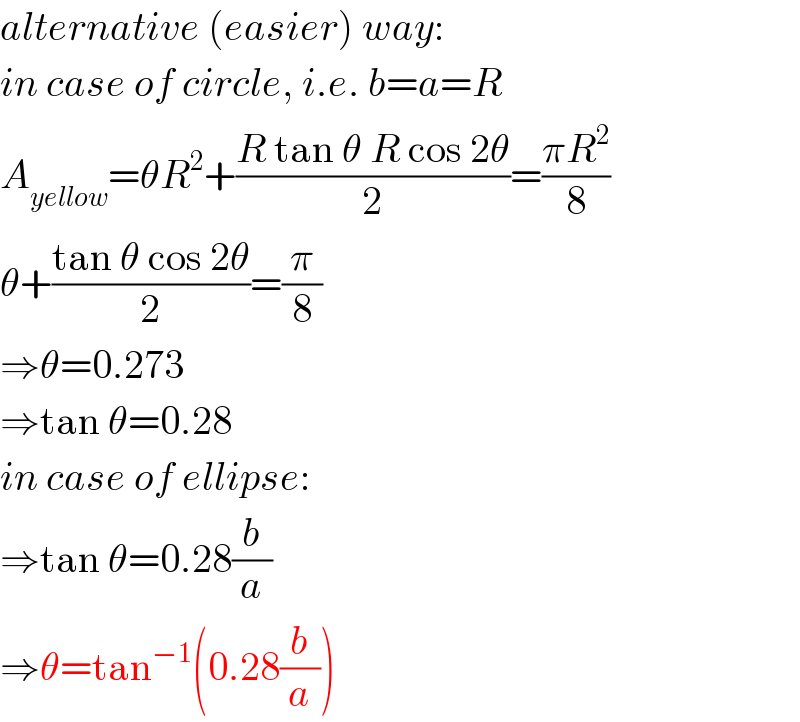
alternative (easier) way: in case of circle, i.e. b=a=R A_(yellow) =θR^2 +((R tan θ R cos 2θ)/2)=((πR^2 )/8) θ+((tan θ cos 2θ)/2)=(π/8) ⇒θ=0.273 ⇒tan θ=0.28 in case of ellipse: ⇒tan θ=0.28(b/a) ⇒θ=tan^(−1) (0.28(b/a))
$${alternative}\:\left({easier}\right)\:{way}: \\ $$$${in}\:{case}\:{of}\:{circle},\:{i}.{e}.\:{b}={a}={R} \\ $$$${A}_{{yellow}} =\theta{R}^{\mathrm{2}} +\frac{{R}\:\mathrm{tan}\:\theta\:{R}\:\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{2}}=\frac{\pi{R}^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\theta+\frac{\mathrm{tan}\:\theta\:\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{2}}=\frac{\pi}{\mathrm{8}} \\ $$$$\Rightarrow\theta=\mathrm{0}.\mathrm{273} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\mathrm{0}.\mathrm{28} \\ $$$${in}\:{case}\:{of}\:{ellipse}: \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\mathrm{0}.\mathrm{28}\frac{{b}}{{a}} \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{0}.\mathrm{28}\frac{{b}}{{a}}\right) \\ $$
Commented by ajfour last updated on 24/Dec/18
seemed impossible to me! SUPERB Sir! Understood. Thank you.
$${seemed}\:{impossible}\:{to}\:{me}! \\ $$$$\mathbb{SUPERB}\:{Sir}!\:\:{Understood}.\:{Thank}\:{you}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *