Question Number 51141 by Tawa1 last updated on 24/Dec/18

Answered by ajfour last updated on 24/Dec/18
Commented by hassentimol last updated on 24/Dec/18
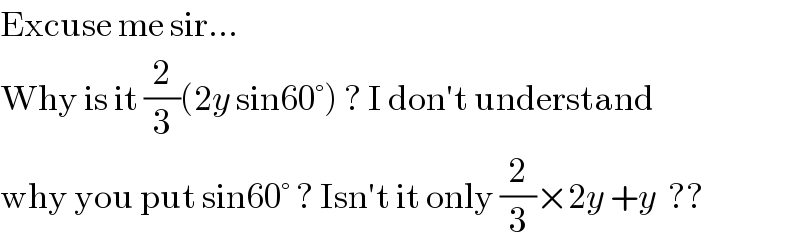
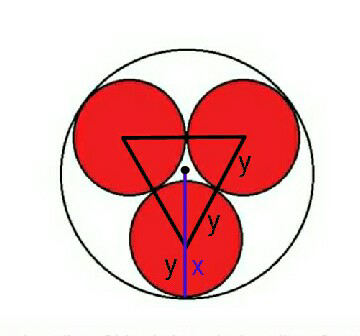
$$\mathrm{Excuse}\:\mathrm{me}\:\mathrm{sir}… \\ $$$$\mathrm{Why}\:\mathrm{is}\:\mathrm{it}\:\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{2}{y}\:\mathrm{sin60}°\right)\:?\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand} \\ $$$$\mathrm{why}\:\mathrm{you}\:\mathrm{put}\:\mathrm{sin60}°\:?\:\mathrm{Isn}'\mathrm{t}\:\mathrm{it}\:\mathrm{only}\:\frac{\mathrm{2}}{\mathrm{3}}×\mathrm{2}{y}\:+{y}\:\:?? \\ $$
Commented by ajfour last updated on 24/Dec/18
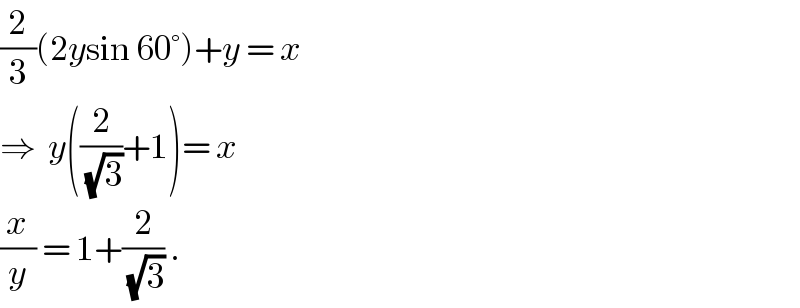
$$\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{2}{y}\mathrm{sin}\:\mathrm{60}°\right)+{y}\:=\:{x} \\ $$$$\Rightarrow\:\:{y}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}+\mathrm{1}\right)=\:{x} \\ $$$$\frac{{x}}{{y}}\:=\:\mathrm{1}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:. \\ $$
Commented by Tawa1 last updated on 24/Dec/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{very}\:\mathrm{short} \\ $$
Commented by hassentimol last updated on 24/Dec/18
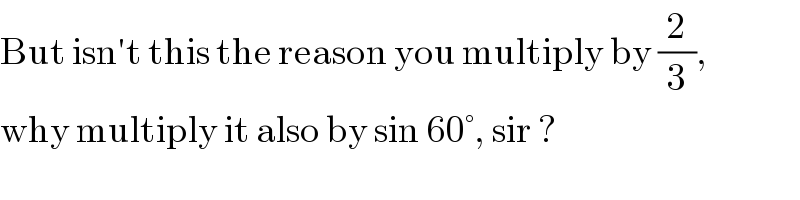
$$\mathrm{But}\:\mathrm{isn}'\mathrm{t}\:\mathrm{this}\:\mathrm{the}\:\mathrm{reason}\:\mathrm{you}\:\mathrm{multiply}\:\mathrm{by}\:\frac{\mathrm{2}}{\mathrm{3}}, \\ $$$$\mathrm{why}\:\mathrm{multiply}\:\mathrm{it}\:\mathrm{also}\:\mathrm{by}\:\mathrm{sin}\:\mathrm{60}°,\:\mathrm{sir}\:? \\ $$
Commented by ajfour last updated on 24/Dec/18
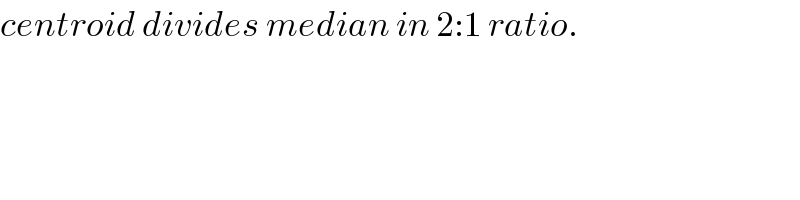
$${centroid}\:{divides}\:{median}\:{in}\:\mathrm{2}:\mathrm{1}\:{ratio}. \\ $$
Commented by ajfour last updated on 24/Dec/18
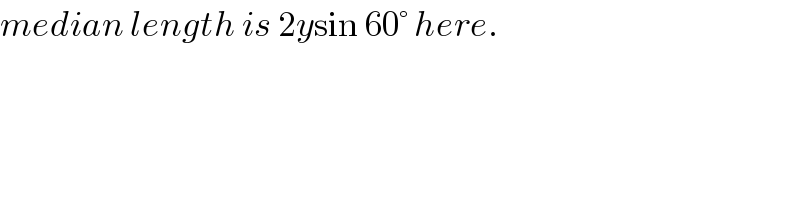
$${median}\:{length}\:{is}\:\mathrm{2}{y}\mathrm{sin}\:\mathrm{60}°\:{here}. \\ $$
Commented by hassentimol last updated on 24/Dec/18
$$\mathrm{Oh}\:!\:\mathrm{I}'\mathrm{ve}\:\mathrm{understood}\:\mathrm{now}.\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}. \\ $$
