Question Number 51153 by Gulay last updated on 24/Dec/18

Commented by Gulay last updated on 24/Dec/18
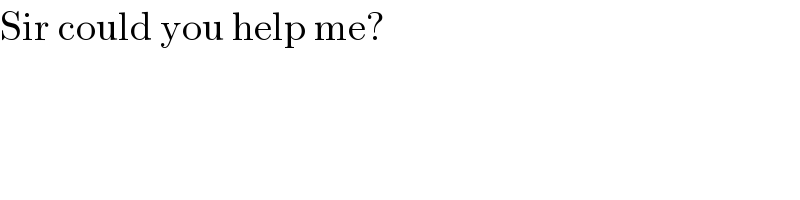
$$\mathrm{Sir}\:\mathrm{could}\:\mathrm{you}\:\mathrm{help}\:\mathrm{me}? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Dec/18
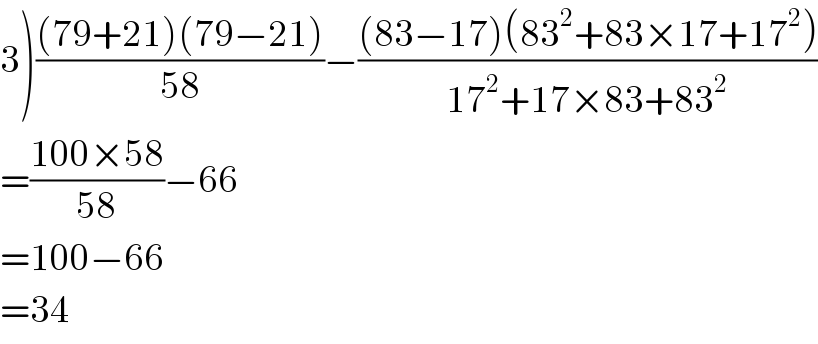
$$\left.\mathrm{3}\right)\frac{\left(\mathrm{79}+\mathrm{21}\right)\left(\mathrm{79}−\mathrm{21}\right)}{\mathrm{58}}−\frac{\left(\mathrm{83}−\mathrm{17}\right)\left(\mathrm{83}^{\mathrm{2}} +\mathrm{83}×\mathrm{17}+\mathrm{17}^{\mathrm{2}} \right)}{\mathrm{17}^{\mathrm{2}} +\mathrm{17}×\mathrm{83}+\mathrm{83}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{100}×\mathrm{58}}{\mathrm{58}}−\mathrm{66} \\ $$$$=\mathrm{100}−\mathrm{66} \\ $$$$=\mathrm{34} \\ $$
Commented by Gulay last updated on 24/Dec/18
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Dec/18
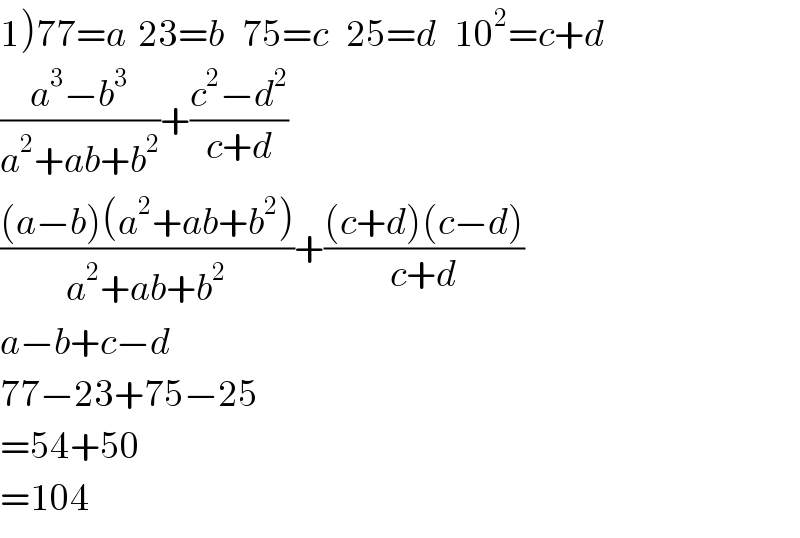
$$\left.\mathrm{1}\right)\mathrm{77}={a}\:\:\mathrm{23}={b}\:\:\:\mathrm{75}={c}\:\:\:\mathrm{25}={d}\:\:\:\mathrm{10}^{\mathrm{2}} ={c}+{d} \\ $$$$\frac{{a}^{\mathrm{3}} −{b}^{\mathrm{3}} }{{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} }+\frac{{c}^{\mathrm{2}} −{d}^{\mathrm{2}} }{{c}+{d}} \\ $$$$\frac{\left({a}−{b}\right)\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)}{{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} }+\frac{\left({c}+{d}\right)\left({c}−{d}\right)}{{c}+{d}} \\ $$$${a}−{b}+{c}−{d} \\ $$$$\mathrm{77}−\mathrm{23}+\mathrm{75}−\mathrm{25} \\ $$$$=\mathrm{54}+\mathrm{50} \\ $$$$=\mathrm{104} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Dec/18
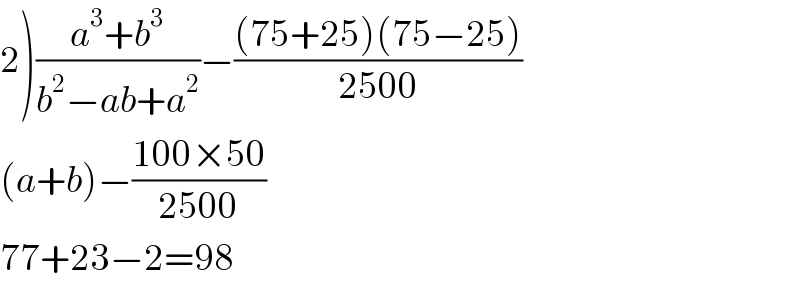
$$\left.\mathrm{2}\right)\frac{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} }{{b}^{\mathrm{2}} −{ab}+{a}^{\mathrm{2}} }−\frac{\left(\mathrm{75}+\mathrm{25}\right)\left(\mathrm{75}−\mathrm{25}\right)}{\mathrm{2500}} \\ $$$$\left({a}+{b}\right)−\frac{\mathrm{100}×\mathrm{50}}{\mathrm{2500}} \\ $$$$\mathrm{77}+\mathrm{23}−\mathrm{2}=\mathrm{98} \\ $$
