Question-51220

Question Number 51220 by Gulay last updated on 25/Dec/18

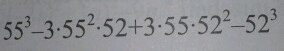
Commented by Gulay last updated on 25/Dec/18

sir help me pls

Answered by afachri last updated on 25/Dec/18

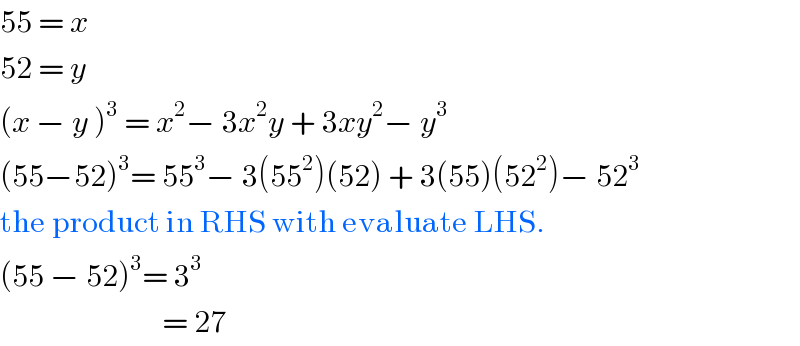
55 = x

52 = y

{(x - y)}^{3} = x^{2} - 3 x^{2} y + 3 {x y}^{2} - y^{3}

{(55 - 52)}^{3} = 55^{3} - 3 (55^{2}) (52) + 3 (55) (52^{2}) - 52^{3}

the product in RHS with evaluate LHS .

{(55 - 52)}^{3} = 3^{3}

= 27

Commented by Gulay last updated on 25/Dec/18

thank you so much sir

Commented by afachri last updated on 25/Dec/18

ur welcome, Sir

Facebook Tweet Pin