Menu Close

Question-51353

Tinku Tara 0 Comments
Pin




Question Number 51353 by behi83417@gmail.com last updated on 26/Dec/18
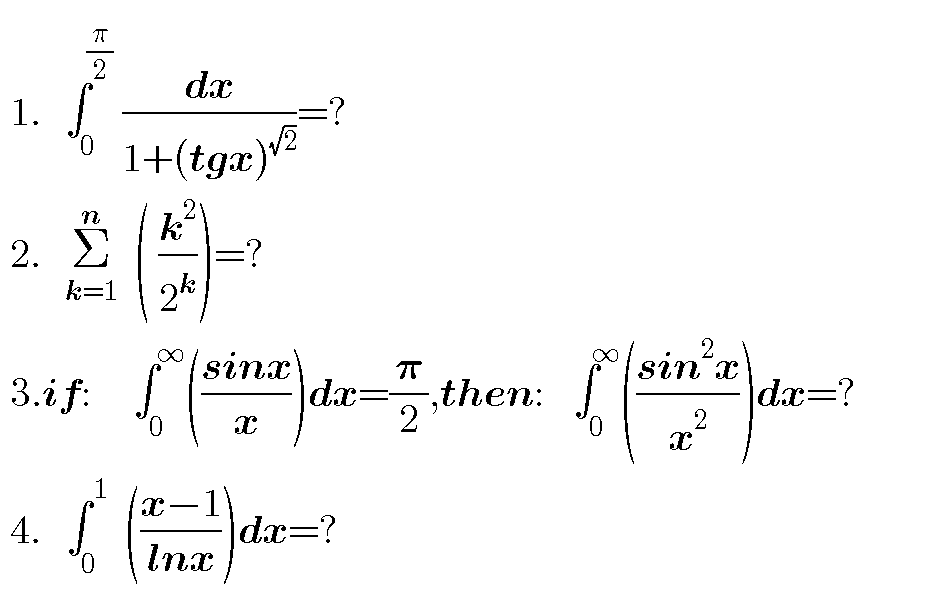
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Dec/18
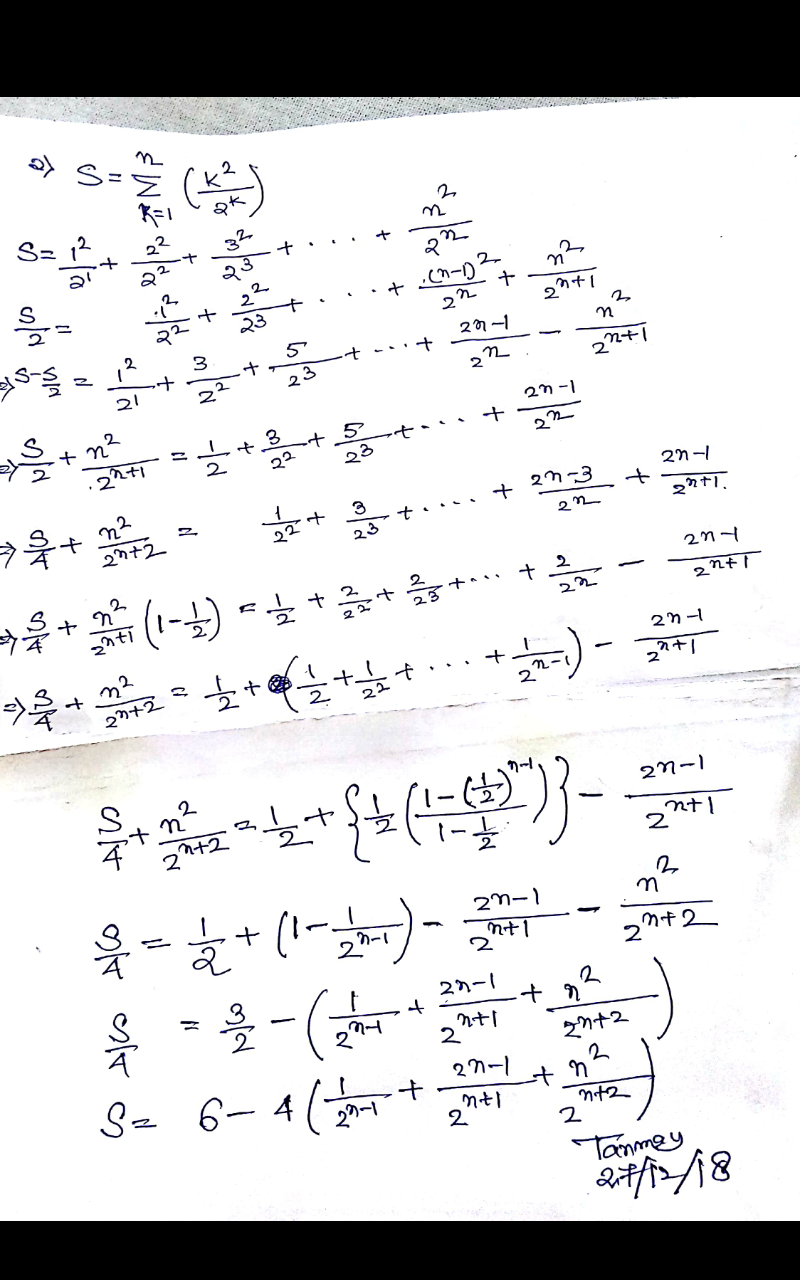
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Dec/18
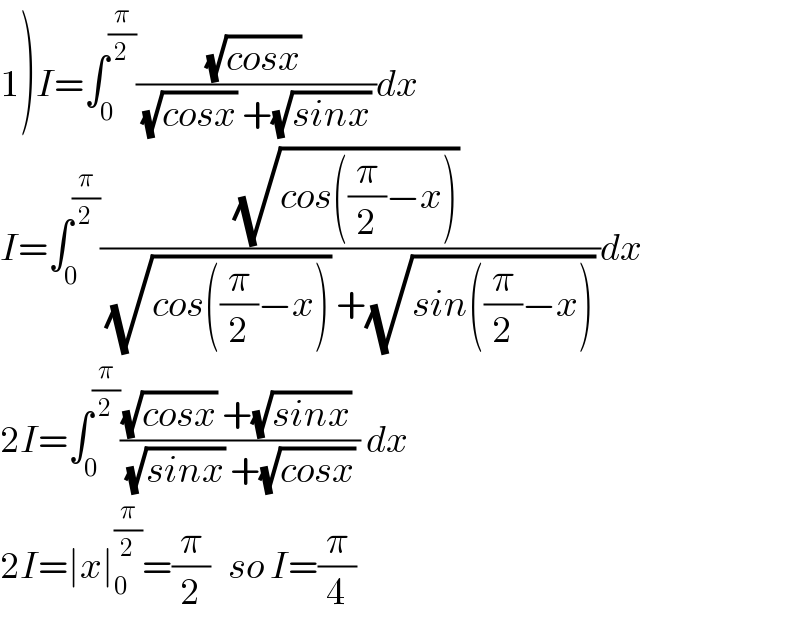
1)I=∫_0 ^(π/2) (((√(cosx)) )/( (√(cosx)) +(√(sinx)) ))dx I=∫_0 ^(π/2) (((√(cos((π/2)−x))) )/( (√(cos((π/2)−x))) +(√(sin((π/2)−x))) ))dx 2I=∫_0 ^(π/2) (((√(cosx)) +(√(sinx)) )/( (√(sinx)) +(√(cosx)) )) dx 2I=∣x∣_0 ^(π/2) =(π/2) so I=(π/4)
$$\left.\mathrm{1}\right){I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\sqrt{{cosx}}\:}{\:\sqrt{{cosx}}\:+\sqrt{{sinx}}\:}{dx} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\sqrt{{cos}\left(\frac{\pi}{\mathrm{2}}−{x}\right)}\:}{\:\sqrt{{cos}\left(\frac{\pi}{\mathrm{2}}−{x}\right)}\:+\sqrt{{sin}\left(\frac{\pi}{\mathrm{2}}−{x}\right)}\:}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\sqrt{{cosx}}\:+\sqrt{{sinx}}\:}{\:\sqrt{{sinx}}\:+\sqrt{{cosx}}\:}\:{dx} \\ $$$$\mathrm{2}{I}=\mid{x}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\frac{\pi}{\mathrm{2}}\:\:\:{so}\:{I}=\frac{\pi}{\mathrm{4}} \\ $$
Commented by behi83417@gmail.com last updated on 26/Dec/18
thank a lot sir tanmay. but the power is: (√2) ...i.e:(tgx)^(√2)
$${thank}\:{a}\:{lot}\:{sir}\:{tanmay}. \\ $$$${but}\:{the}\:{power}\:{is}:\:\:\sqrt{\mathrm{2}}\:\:…{i}.{e}:\left({tgx}\right)^{\sqrt{\mathrm{2}}} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 26/Dec/18
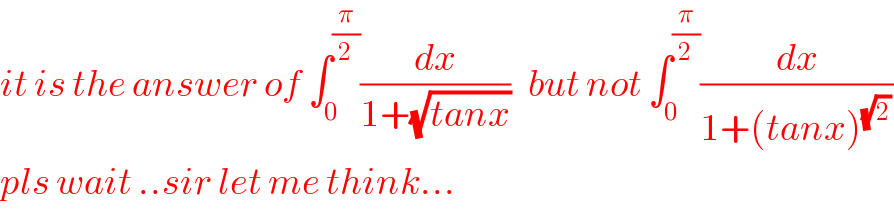
it is the answer of ∫_0 ^(π/2) (dx/(1+(√(tanx)))) but not ∫_0 ^(π/2) (dx/(1+(tanx)^((√2) ) )) pls wait ..sir let me think...
$${it}\:{is}\:{the}\:{answer}\:{of}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{1}+\sqrt{{tanx}}}\:\:\:{but}\:{not}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{1}+\left({tanx}\right)^{\sqrt{\mathrm{2}}\:} } \\ $$$${pls}\:{wait}\:..{sir}\:{let}\:{me}\:{think}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Dec/18
4)∫_0 ^1 ((x^a −1)/(lnx))dx I(a)=∫_0 ^1 ((x^a −1)/(lnx))dx ((dI(a))/da)=∫_0 ^1 (∂/∂a)(((x^a −1)/(lnx)))dx =∫_0 ^1 ((x^a lnx)/(lnx))dx =∣(x^(a+1) /(a+1))∣_0 ^1 =(1/(a+1)) ∫dI(a)=∫(da/(a+1)) I(a)=ln(a+1)+c when a=0 I(a)=0 [∫((x^0 −1)/(lnx))dx=0] c=0 I(a)=ln(a+1) hence I=ln2 when a=1
$$\left.\mathrm{4}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} −\mathrm{1}}{{lnx}}{dx} \\ $$$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} −\mathrm{1}}{{lnx}}{dx} \\ $$$$\frac{{dI}\left({a}\right)}{{da}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\partial}{\partial{a}}\left(\frac{{x}^{{a}} −\mathrm{1}}{{lnx}}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} {lnx}}{{lnx}}{dx} \\ $$$$=\mid\frac{{x}^{{a}+\mathrm{1}} }{{a}+\mathrm{1}}\mid_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{{a}+\mathrm{1}} \\ $$$$\int{dI}\left({a}\right)=\int\frac{{da}}{{a}+\mathrm{1}} \\ $$$${I}\left({a}\right)={ln}\left({a}+\mathrm{1}\right)+{c} \\ $$$${when}\:\:{a}=\mathrm{0}\:\:\:\:\:\:\:\:{I}\left({a}\right)=\mathrm{0}\:\:\:\left[\int\frac{{x}^{\mathrm{0}} −\mathrm{1}}{{lnx}}{dx}=\mathrm{0}\right] \\ $$$${c}=\mathrm{0} \\ $$$${I}\left({a}\right)={ln}\left({a}+\mathrm{1}\right) \\ $$$${hence}\:{I}={ln}\mathrm{2}\:\:{when}\:{a}=\mathrm{1} \\ $$
Answered by mr W last updated on 26/Dec/18
(3) ∫((sin^2 x)/x^2 ) dx =−∫sin^2 x d((1/x)) =−((sin^2 x)/x)+∫((2 sin x cos x)/x) dx =−((sin^2 x)/x)+∫((sin 2x)/x) dx =−((sin^2 x)/x)+∫((sin 2x)/(2x)) d(2x) ∫_0 ^∞ ((sin^2 x)/x^2 ) dx =−[((sin^2 x)/x)]_0 ^∞ +∫_0 ^∞ ((sin 2x)/(2x)) d(2x) =0+∫_0 ^∞ ((sin t)/t) dt =(π/2)
$$\left(\mathrm{3}\right) \\ $$$$\int\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{{x}^{\mathrm{2}} }\:{dx} \\ $$$$=−\int\mathrm{sin}^{\mathrm{2}} \:{x}\:{d}\left(\frac{\mathrm{1}}{{x}}\right) \\ $$$$=−\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{{x}}+\int\frac{\mathrm{2}\:\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}{{x}}\:{dx} \\ $$$$=−\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{{x}}+\int\frac{\mathrm{sin}\:\mathrm{2}{x}}{{x}}\:{dx} \\ $$$$=−\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{{x}}+\int\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{2}{x}}\:{d}\left(\mathrm{2}{x}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{{x}^{\mathrm{2}} }\:{dx} \\ $$$$=−\left[\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{{x}}\right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{2}{x}}\:{d}\left(\mathrm{2}{x}\right) \\ $$$$=\mathrm{0}+\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\:{t}}{{t}}\:{dt} \\ $$$$=\frac{\pi}{\mathrm{2}} \\ $$
Commented by behi83417@gmail.com last updated on 26/Dec/18
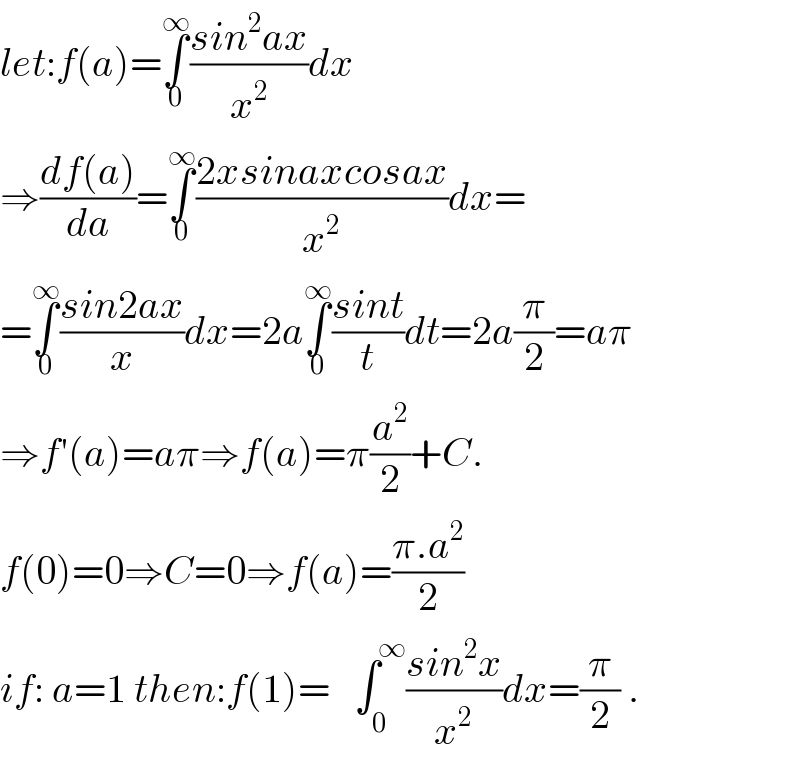
let:f(a)=∫_0 ^∞ ((sin^2 ax)/x^2 )dx ⇒((df(a))/da)=∫_0 ^∞ ((2xsinaxcosax)/x^2 )dx= =∫_0 ^∞ ((sin2ax)/x)dx=2a∫_0 ^∞ ((sint)/t)dt=2a(π/2)=aπ ⇒f′(a)=aπ⇒f(a)=π(a^2 /2)+C. f(0)=0⇒C=0⇒f(a)=((π.a^2 )/2) if: a=1 then:f(1)=∫_( 0) ^( ∞) ((sin^2 x)/x^2 )dx=(π/2) .
$${let}:{f}\left({a}\right)=\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{sin}^{\mathrm{2}} {ax}}{{x}^{\mathrm{2}} }{dx} \\ $$$$\Rightarrow\frac{{df}\left({a}\right)}{{da}}=\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{2}{xsinaxcosax}}{{x}^{\mathrm{2}} }{dx}= \\ $$$$=\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{sin}\mathrm{2}{ax}}{{x}}{dx}=\mathrm{2}{a}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{sint}}{{t}}{dt}=\mathrm{2}{a}\frac{\pi}{\mathrm{2}}={a}\pi \\ $$$$\Rightarrow{f}'\left({a}\right)={a}\pi\Rightarrow{f}\left({a}\right)=\pi\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+{C}. \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow{C}=\mathrm{0}\Rightarrow{f}\left({a}\right)=\frac{\pi.{a}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${if}:\:{a}=\mathrm{1}\:{then}:{f}\left(\mathrm{1}\right)=\underset{\:\:\:\:\:\:\mathrm{0}} {\overset{\:\:\:\:\:\:\:\:\:\:\:\:\infty} {\int}}\frac{{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }{dx}=\frac{\pi}{\mathrm{2}}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Dec/18
1)∫_0 ^(π/2) (dx/(1+(tanx)^a )) [[ a=(√2) ] ∫_0 ^(π/2) (dx/(1+(((sinx)^a )/((cosx)^a )))) I=∫_0 ^(π/2) (((cosx)^a )/((sinx)^a +(cosx)^a ))dx now using ∫_0 ^(π/2) f(x)dx =∫_0 ^(π/2) f((π/2)−x)dx 2I=∫_0 ^(π/2) dx I=(π/4)
$$\left.\mathrm{1}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{1}+\left({tanx}\right)^{{a}} }\:\:\:\:\:\:\:\:\left[\left[\:{a}=\sqrt{\mathrm{2}}\:\right]\right. \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{1}+\frac{\left({sinx}\right)^{{a}} }{\left({cosx}\right)^{{a}} }} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left({cosx}\right)^{{a}} }{\left({sinx}\right)^{{a}} +\left({cosx}\right)^{{a}} }{dx} \\ $$$${now}\:{using}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {f}\left({x}\right){dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {f}\left(\frac{\pi}{\mathrm{2}}−{x}\right){dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx}\:\:\:{I}=\frac{\pi}{\mathrm{4}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *