Question Number 51372 by ajfour last updated on 26/Dec/18
Commented by ajfour last updated on 26/Dec/18

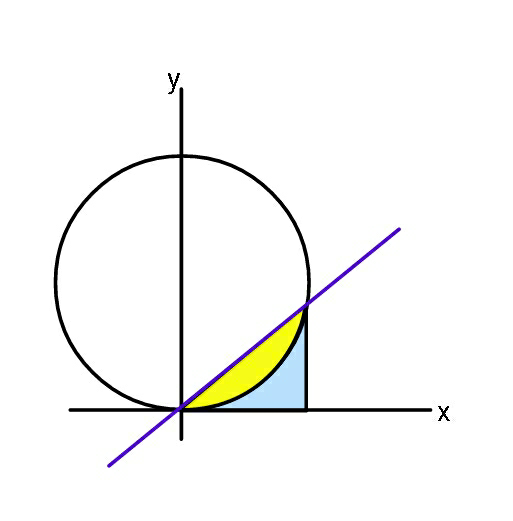
$${For}\:{the}\:{two}\:{coloured}\:{areas}\:{to}\:{be} \\ $$$${equal},\:{what}\:{is}\:{the}\:{slope}\:{of}\:{blue}\:{line}? \\ $$
Answered by mr W last updated on 26/Dec/18
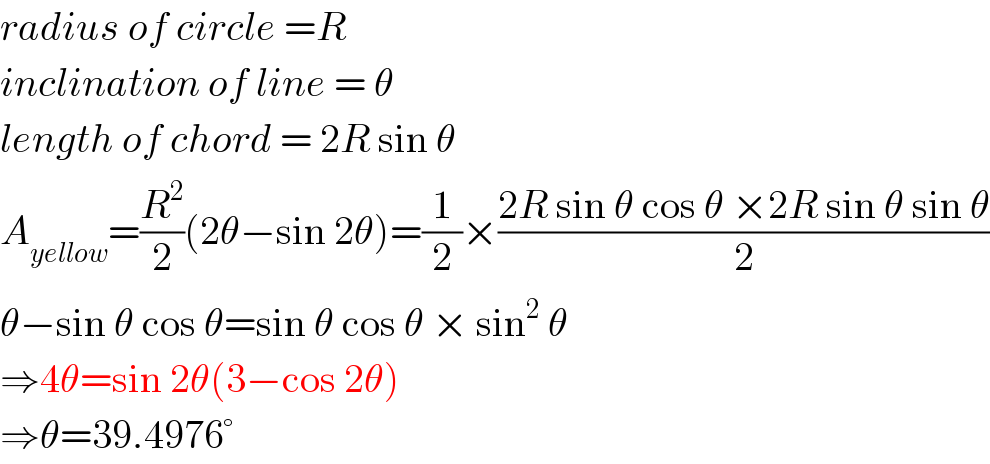
$${radius}\:{of}\:{circle}\:={R} \\ $$$${inclination}\:{of}\:{line}\:=\:\theta \\ $$$${length}\:{of}\:{chord}\:=\:\mathrm{2}{R}\:\mathrm{sin}\:\theta \\ $$$${A}_{{yellow}} =\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\theta−\mathrm{sin}\:\mathrm{2}\theta\right)=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}{R}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\:×\mathrm{2}{R}\:\mathrm{sin}\:\theta\:\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$$\theta−\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta=\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\:×\:\mathrm{sin}^{\mathrm{2}} \:\theta \\ $$$$\Rightarrow\mathrm{4}\theta=\mathrm{sin}\:\mathrm{2}\theta\left(\mathrm{3}−\mathrm{cos}\:\mathrm{2}\theta\right) \\ $$$$\Rightarrow\theta=\mathrm{39}.\mathrm{4976}° \\ $$
Commented by ajfour last updated on 26/Dec/18
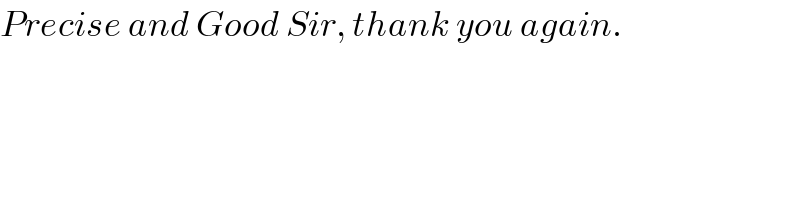
$${Precise}\:{and}\:{Good}\:{Sir},\:{thank}\:{you}\:{again}. \\ $$
