Question Number 51466 by mr W last updated on 27/Dec/18
Commented by mr W last updated on 27/Dec/18
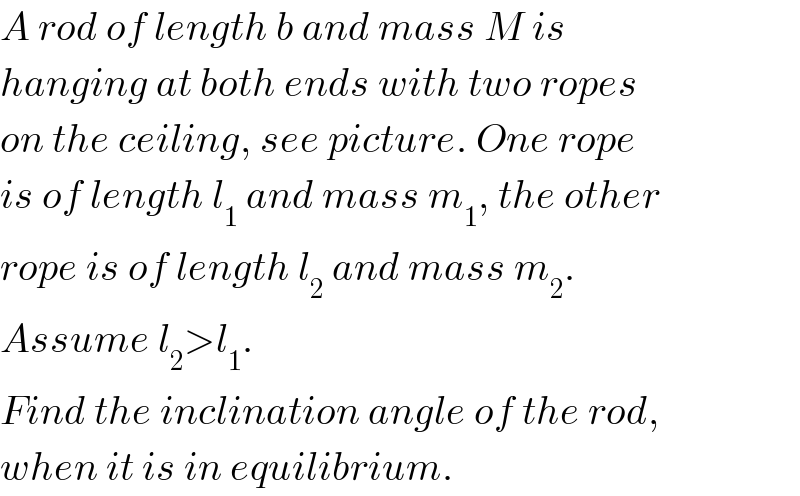
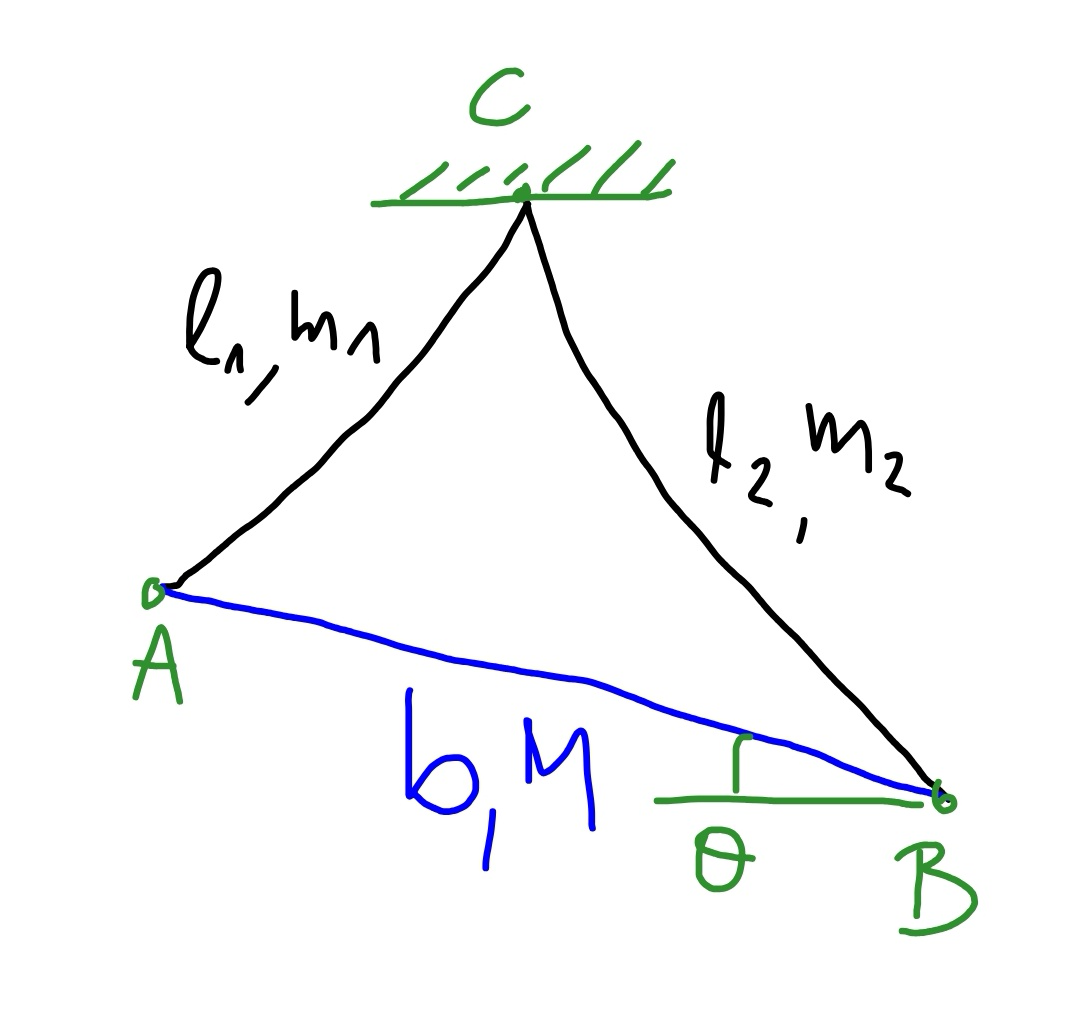
$${A}\:{rod}\:{of}\:{length}\:{b}\:{and}\:{mass}\:{M}\:{is} \\ $$$${hanging}\:{at}\:{both}\:{ends}\:{with}\:{two}\:{ropes} \\ $$$${on}\:{the}\:{ceiling},\:{see}\:{picture}.\:{One}\:{rope} \\ $$$${is}\:{of}\:{length}\:{l}_{\mathrm{1}} \:{and}\:{mass}\:{m}_{\mathrm{1}} ,\:{the}\:{other} \\ $$$${rope}\:{is}\:{of}\:{length}\:{l}_{\mathrm{2}} \:{and}\:{mass}\:{m}_{\mathrm{2}} .\: \\ $$$${Assume}\:{l}_{\mathrm{2}} >{l}_{\mathrm{1}} . \\ $$$${Find}\:{the}\:{inclination}\:{angle}\:{of}\:{the}\:{rod}, \\ $$$${when}\:{it}\:{is}\:{in}\:{equilibrium}. \\ $$
Commented by ajfour last updated on 28/Dec/18
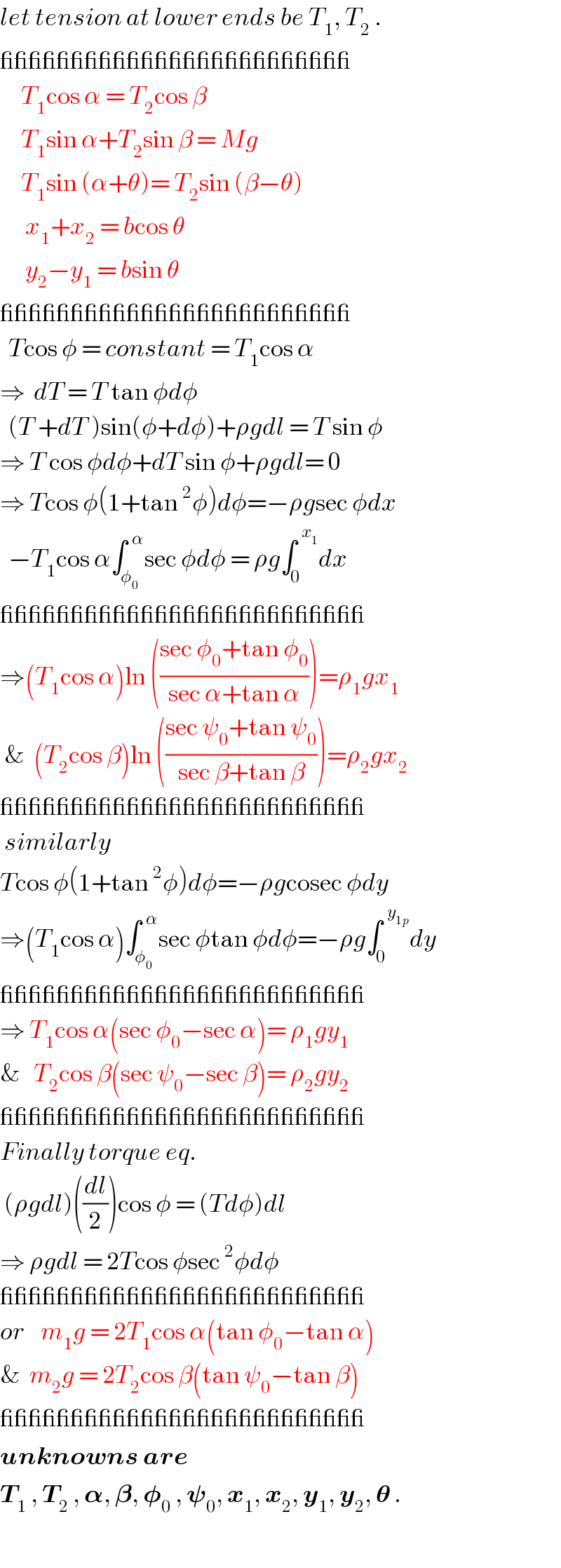
$${let}\:{tension}\:{at}\:{lower}\:{ends}\:{be}\:{T}_{\mathrm{1}} ,\:{T}_{\mathrm{2}} \:. \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:\:\:\:{T}_{\mathrm{1}} \mathrm{cos}\:\alpha\:=\:{T}_{\mathrm{2}} \mathrm{cos}\:\beta \\ $$$$\:\:\:\:\:{T}_{\mathrm{1}} \mathrm{sin}\:\alpha+{T}_{\mathrm{2}} \mathrm{sin}\:\beta\:=\:{Mg} \\ $$$$\:\:\:\:\:{T}_{\mathrm{1}} \mathrm{sin}\:\left(\alpha+\theta\right)=\:{T}_{\mathrm{2}} \mathrm{sin}\:\left(\beta−\theta\right) \\ $$$$\:\:\:\:\:\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} \:=\:{b}\mathrm{cos}\:\theta \\ $$$$\:\:\:\:\:\:{y}_{\mathrm{2}} −{y}_{\mathrm{1}} \:=\:{b}\mathrm{sin}\:\theta \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:{T}\mathrm{cos}\:\phi\:=\:{constant}\:=\:{T}_{\mathrm{1}} \mathrm{cos}\:\alpha \\ $$$$\Rightarrow\:\:{dT}\:=\:{T}\:\mathrm{tan}\:\phi{d}\phi \\ $$$$\:\:\left({T}\:+{dT}\:\right)\mathrm{sin}\left(\phi+{d}\phi\right)+\rho{gdl}\:=\:{T}\:\mathrm{sin}\:\phi \\ $$$$\Rightarrow\:{T}\:\mathrm{cos}\:\phi{d}\phi+{dT}\:\mathrm{sin}\:\phi+\rho{gdl}=\:\mathrm{0} \\ $$$$\Rightarrow\:{T}\mathrm{cos}\:\phi\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \phi\right){d}\phi=−\rho{g}\mathrm{sec}\:\phi{dx} \\ $$$$\:\:−{T}_{\mathrm{1}} \mathrm{cos}\:\alpha\int_{\phi_{\mathrm{0}} } ^{\:\:\alpha} \mathrm{sec}\:\phi{d}\phi\:=\:\rho{g}\int_{\mathrm{0}} ^{\:\:{x}_{\mathrm{1}} } {dx} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\left({T}_{\mathrm{1}} \mathrm{cos}\:\alpha\right)\mathrm{ln}\:\left(\frac{\mathrm{sec}\:\phi_{\mathrm{0}} +\mathrm{tan}\:\phi_{\mathrm{0}} }{\mathrm{sec}\:\alpha+\mathrm{tan}\:\alpha}\right)=\rho_{\mathrm{1}} {gx}_{\mathrm{1}} \\ $$$$\:\&\:\:\left({T}_{\mathrm{2}} \mathrm{cos}\:\beta\right)\mathrm{ln}\:\left(\frac{\mathrm{sec}\:\psi_{\mathrm{0}} +\mathrm{tan}\:\psi_{\mathrm{0}} }{\mathrm{sec}\:\beta+\mathrm{tan}\:\beta}\right)=\rho_{\mathrm{2}} {gx}_{\mathrm{2}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:{similarly} \\ $$$${T}\mathrm{cos}\:\phi\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \phi\right){d}\phi=−\rho{g}\mathrm{cosec}\:\phi{dy} \\ $$$$\Rightarrow\left({T}_{\mathrm{1}} \mathrm{cos}\:\alpha\right)\int_{\phi_{\mathrm{0}} } ^{\:\:\alpha} \mathrm{sec}\:\phi\mathrm{tan}\:\phi{d}\phi=−\rho{g}\int_{\mathrm{0}} ^{\:\:{y}_{\mathrm{1}{p}} } {dy} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:{T}_{\mathrm{1}} \mathrm{cos}\:\alpha\left(\mathrm{sec}\:\phi_{\mathrm{0}} −\mathrm{sec}\:\alpha\right)=\:\rho_{\mathrm{1}} {gy}_{\mathrm{1}} \\ $$$$\&\:\:\:{T}_{\mathrm{2}} \mathrm{cos}\:\beta\left(\mathrm{sec}\:\psi_{\mathrm{0}} −\mathrm{sec}\:\beta\right)=\:\rho_{\mathrm{2}} {gy}_{\mathrm{2}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${Finally}\:{torque}\:{eq}. \\ $$$$\:\left(\rho{gdl}\right)\left(\frac{{dl}}{\mathrm{2}}\right)\mathrm{cos}\:\phi\:=\:\left({Td}\phi\right){dl} \\ $$$$\Rightarrow\:\rho{gdl}\:=\:\mathrm{2}{T}\mathrm{cos}\:\phi\mathrm{sec}\:^{\mathrm{2}} \phi{d}\phi \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${or}\:\:\:\:{m}_{\mathrm{1}} {g}\:=\:\mathrm{2}{T}_{\mathrm{1}} \mathrm{cos}\:\alpha\left(\mathrm{tan}\:\phi_{\mathrm{0}} −\mathrm{tan}\:\alpha\right) \\ $$$$\&\:\:{m}_{\mathrm{2}} {g}\:=\:\mathrm{2}{T}_{\mathrm{2}} \mathrm{cos}\:\beta\left(\mathrm{tan}\:\psi_{\mathrm{0}} −\mathrm{tan}\:\beta\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\boldsymbol{{unknowns}}\:\boldsymbol{{are}} \\ $$$$\boldsymbol{{T}}_{\mathrm{1}} \:,\:\boldsymbol{{T}}_{\mathrm{2}} \:,\:\boldsymbol{\alpha},\:\boldsymbol{\beta},\:\boldsymbol{\phi}_{\mathrm{0}} \:,\:\boldsymbol{\psi}_{\mathrm{0}} ,\:\boldsymbol{{x}}_{\mathrm{1}} ,\:\boldsymbol{{x}}_{\mathrm{2}} ,\:\boldsymbol{{y}}_{\mathrm{1}} ,\:\boldsymbol{{y}}_{\mathrm{2}} ,\:\boldsymbol{\theta}\:. \\ $$
Commented by ajfour last updated on 27/Dec/18
Commented by ajfour last updated on 28/Dec/18
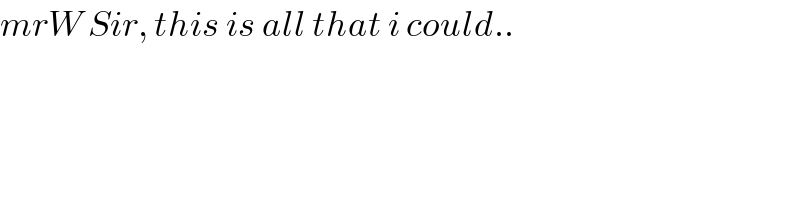
$${mrW}\:{Sir},\:{this}\:{is}\:{all}\:{that}\:{i}\:{could}.. \\ $$
Commented by mr W last updated on 29/Dec/18

$${thank}\:{you}\:{so}\:{far}\:{sir}!\: \\ $$$${i}\:{got}\:{a}\:{solution}\:{using}\:{catenary}\:{method}. \\ $$
Answered by mr W last updated on 28/Dec/18
Commented by mr W last updated on 28/Dec/18
Commented by mr W last updated on 29/Dec/18
![rod AB: length b, mass M rope 1: length l_1 , mass m_1 , ρ_1 =m_1 /l_1 rope 2: length l_2 , mass m_2 , ρ_2 =m_2 /l_2 At point A: tension in rope 1 = T_A axialforce in rod = N_A T_A =((Mg cos θ)/(2 sin (α+θ)))=((Mg)/(2 (sin α+cos α tan θ))) N_A =((Mg cos α)/(2 sin (α+θ)))=((Mg)/(2 (tan α cos θ+sin θ))) horizontal component in rope 1 = T_(10) T_(10) =T_A cos α=((Mg)/(2 (tan α+tan θ))) a_1 =(T_(10) /(ρ_1 g))=((Ml_1 )/(2(tan α+tan θ)m_1 )) eqn. of rope 1: y=a_1 cosh (x/a_1 ) y′=sinh (x/a_1 ) s=a_1 sinh (x/a_1 ) (length of rope upon O) at A: y_A =a_1 cosh (e_1 /a_1 ) y′_A =sinh (e_1 /a_1 )=tan α ⇒ (e_1 /a_1 )=sinh^(−1) (tan α) s_A =a_1 sinh (e_1 /a_1 )=a_1 tan α ⇒y_A =a_1 cosh (e_1 /a_1 )=a_1 cosh [sinh^(−1) (tan α)] at C: y_C =a_1 cosh ((e_1 +f_1 )/a_1 )=a_1 cosh [sinh^(−1) (tan α)+(f_1 /a_1 )] =y_A +h_1 =a_1 cosh [sinh^(−1) (tan α)]+h_1 ⇒a_1 cosh [sinh^(−1) (tan α)+(f_1 /a_1 )]−a_1 cosh [sinh^(−1) (tan α)]=h_1 s_C =a_1 sinh ((e_1 +f_1 )/a_1 )=a_1 sinh [sinh^(−1) (tan α)+(f_1 /a_1 )] =s_A +l_1 =a_1 tan α+l_1 ⇒sinh [sinh^(−1) (tan α)+(f_1 /a_1 )]=tan α+(l_1 /a_1 ) ⇒sinh^(−1) (tan α)+(f_1 /a_1 )=sinh^(−1) (tan α+(l_1 /a_1 )) ⇒(f_1 /a_1 )=sinh^(−1) (tan α+(l_1 /a_1 ))−sinh^(−1) (tan α) ⇒a_1 cosh [sinh^(−1) (tan α+(l_1 /a_1 ))]−a_1 cosh [sinh^(−1) (tan α)]=h_1 At point B: tension in rope 2 = T_B axialforce in rod = N_B T_A =((Mg cos θ)/(2 sin (β−θ)))=((Mg)/(2 (sin β−cos β tan θ))) N_B =((Mg cos β)/(2 sin (β−θ)))=((Mg)/(2 (tan β cos θ−sin θ))) horizontal component in rope 2 = T_(20) T_(20) =T_B cos β=((Mg)/(2 (tan β−tan θ))) a_2 =(T_(20) /(ρ_2 g))=((Ml_2 )/(2(tan β−tan θ)m_2 )) eqn. of rope 2: y=a_2 cosh (x/a_2 ) y′=sinh (x/a_2 ) s=a_2 sinh (x/a_2 ) (length of rope upon O) at B: y_B =a_2 cosh (e_2 /a_2 ) y′_B =sinh (e_2 /a_2 )=tan β ⇒ (e_2 /a_2 )=sinh^(−1) (tan β) s_B =a_2 sinh (e_2 /a_2 )=a_2 tan β ⇒y_B =a_2 cosh (e_2 /a_2 )=a_2 cosh [sinh^(−1) (tan β)] at C: y_C =a_2 cosh ((e_2 +f_2 )/a_2 )=a_2 cosh [sinh^(−1) (tan β)+(f_2 /a_2 )] =y_B +h_2 =a_2 cosh [sinh^(−1) (tan β)]+h_2 ⇒a_2 cosh [sinh^(−1) (tan β)+(f_2 /a_2 )]−a_2 cosh [sinh^(−1) (tan β)]=h_2 s_C =a_2 sinh ((e_2 +f_2 )/a_2 )=a_2 sinh [sinh^(−1) (tan β)+(f_2 /a_2 )] =s_A +l_2 =a_2 tan β+l_2 ....... to be continued ......](https://www.tinkutara.com/question/Q51599.png)
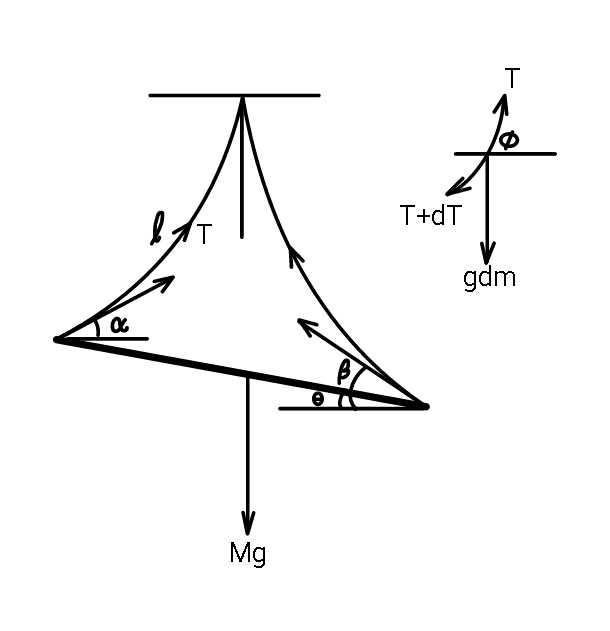
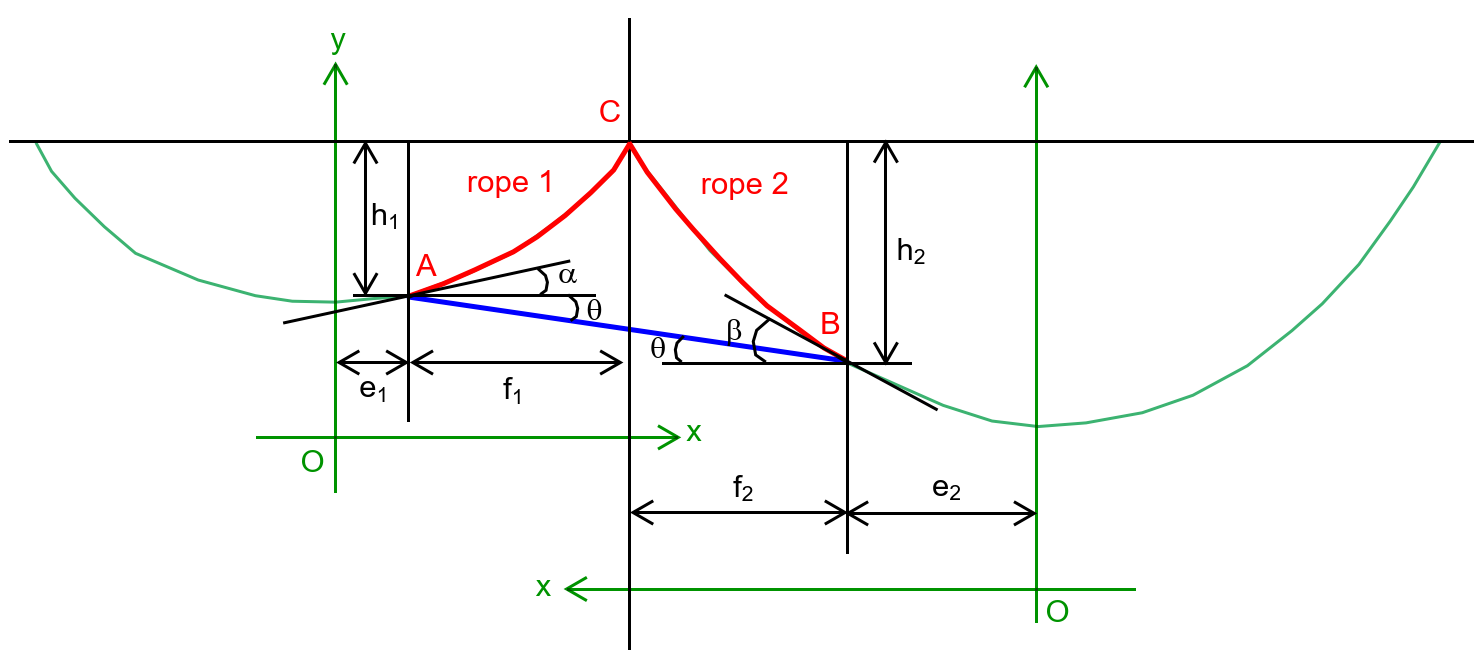
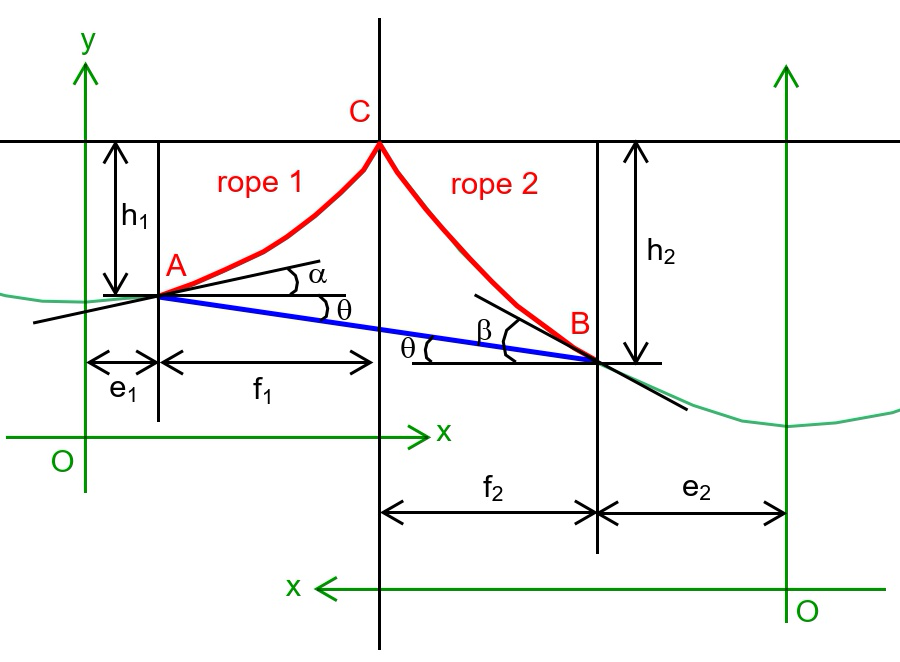
$${rod}\:{AB}:\:{length}\:{b},\:{mass}\:{M} \\ $$$${rope}\:\mathrm{1}:\:{length}\:{l}_{\mathrm{1}} ,\:{mass}\:{m}_{\mathrm{1}} ,\:\rho_{\mathrm{1}} ={m}_{\mathrm{1}} /{l}_{\mathrm{1}} \\ $$$${rope}\:\mathrm{2}:\:{length}\:{l}_{\mathrm{2}} ,\:{mass}\:{m}_{\mathrm{2}} ,\:\rho_{\mathrm{2}} ={m}_{\mathrm{2}} /{l}_{\mathrm{2}} \\ $$$$\boldsymbol{{At}}\:\boldsymbol{{point}}\:\boldsymbol{{A}}: \\ $$$${tension}\:{in}\:{rope}\:\mathrm{1}\:=\:{T}_{{A}} \\ $$$${axialforce}\:{in}\:{rod}\:=\:{N}_{{A}} \\ $$$${T}_{{A}} =\frac{{Mg}\:\mathrm{cos}\:\theta}{\mathrm{2}\:\mathrm{sin}\:\left(\alpha+\theta\right)}=\frac{{Mg}}{\mathrm{2}\:\left(\mathrm{sin}\:\alpha+\mathrm{cos}\:\alpha\:\mathrm{tan}\:\theta\right)} \\ $$$${N}_{{A}} =\frac{{Mg}\:\mathrm{cos}\:\alpha}{\mathrm{2}\:\mathrm{sin}\:\left(\alpha+\theta\right)}=\frac{{Mg}}{\mathrm{2}\:\left(\mathrm{tan}\:\alpha\:\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)} \\ $$$${horizontal}\:{component}\:{in}\:{rope}\:\mathrm{1}\:=\:{T}_{\mathrm{10}} \\ $$$${T}_{\mathrm{10}} ={T}_{{A}} \:\mathrm{cos}\:\alpha=\frac{{Mg}}{\mathrm{2}\:\left(\mathrm{tan}\:\alpha+\mathrm{tan}\:\theta\right)} \\ $$$${a}_{\mathrm{1}} =\frac{{T}_{\mathrm{10}} }{\rho_{\mathrm{1}} {g}}=\frac{{Ml}_{\mathrm{1}} }{\mathrm{2}\left(\mathrm{tan}\:\alpha+\mathrm{tan}\:\theta\right){m}_{\mathrm{1}} } \\ $$$${eqn}.\:{of}\:{rope}\:\mathrm{1}: \\ $$$${y}={a}_{\mathrm{1}} \mathrm{cosh}\:\frac{{x}}{{a}_{\mathrm{1}} } \\ $$$${y}'=\mathrm{sinh}\:\frac{{x}}{{a}_{\mathrm{1}} } \\ $$$${s}={a}_{\mathrm{1}} \mathrm{sinh}\:\frac{{x}}{{a}_{\mathrm{1}} }\:\:\:\:\:\left({length}\:{of}\:{rope}\:{upon}\:{O}\right) \\ $$$${at}\:{A}: \\ $$$${y}_{{A}} ={a}_{\mathrm{1}} \mathrm{cosh}\:\frac{{e}_{\mathrm{1}} }{{a}_{\mathrm{1}} } \\ $$$${y}'_{{A}} =\mathrm{sinh}\:\frac{{e}_{\mathrm{1}} }{{a}_{\mathrm{1}} }=\mathrm{tan}\:\alpha\:\Rightarrow\:\frac{{e}_{\mathrm{1}} }{{a}_{\mathrm{1}} }=\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right) \\ $$$${s}_{{A}} ={a}_{\mathrm{1}} \mathrm{sinh}\:\frac{{e}_{\mathrm{1}} }{{a}_{\mathrm{1}} }={a}_{\mathrm{1}} \mathrm{tan}\:\alpha \\ $$$$\Rightarrow{y}_{{A}} ={a}_{\mathrm{1}} \mathrm{cosh}\:\frac{{e}_{\mathrm{1}} }{{a}_{\mathrm{1}} }={a}_{\mathrm{1}} \mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)\right] \\ $$$${at}\:{C}: \\ $$$${y}_{{C}} ={a}_{\mathrm{1}} \mathrm{cosh}\:\frac{{e}_{\mathrm{1}} +{f}_{\mathrm{1}} }{{a}_{\mathrm{1}} }={a}_{\mathrm{1}} \mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)+\frac{{f}_{\mathrm{1}} }{{a}_{\mathrm{1}} }\right] \\ $$$$={y}_{{A}} +{h}_{\mathrm{1}} ={a}_{\mathrm{1}} \mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)\right]+{h}_{\mathrm{1}} \\ $$$$\Rightarrow{a}_{\mathrm{1}} \mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)+\frac{{f}_{\mathrm{1}} }{{a}_{\mathrm{1}} }\right]−{a}_{\mathrm{1}} \mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)\right]={h}_{\mathrm{1}} \\ $$$${s}_{{C}} ={a}_{\mathrm{1}} \mathrm{sinh}\:\frac{{e}_{\mathrm{1}} +{f}_{\mathrm{1}} }{{a}_{\mathrm{1}} }={a}_{\mathrm{1}} \mathrm{sinh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)+\frac{{f}_{\mathrm{1}} }{{a}_{\mathrm{1}} }\right] \\ $$$$={s}_{{A}} +{l}_{\mathrm{1}} ={a}_{\mathrm{1}} \mathrm{tan}\:\alpha+{l}_{\mathrm{1}} \\ $$$$\Rightarrow\mathrm{sinh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)+\frac{{f}_{\mathrm{1}} }{{a}_{\mathrm{1}} }\right]=\mathrm{tan}\:\alpha+\frac{{l}_{\mathrm{1}} }{{a}_{\mathrm{1}} } \\ $$$$\Rightarrow\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)+\frac{{f}_{\mathrm{1}} }{{a}_{\mathrm{1}} }=\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}_{\mathrm{1}} }{{a}_{\mathrm{1}} }\right) \\ $$$$\Rightarrow\frac{{f}_{\mathrm{1}} }{{a}_{\mathrm{1}} }=\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}_{\mathrm{1}} }{{a}_{\mathrm{1}} }\right)−\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right) \\ $$$$\Rightarrow{a}_{\mathrm{1}} \mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}_{\mathrm{1}} }{{a}_{\mathrm{1}} }\right)\right]−{a}_{\mathrm{1}} \mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)\right]={h}_{\mathrm{1}} \\ $$$$\boldsymbol{{At}}\:\boldsymbol{{point}}\:\boldsymbol{{B}}: \\ $$$${tension}\:{in}\:{rope}\:\mathrm{2}\:=\:{T}_{{B}} \\ $$$${axialforce}\:{in}\:{rod}\:=\:{N}_{{B}} \\ $$$${T}_{{A}} =\frac{{Mg}\:\mathrm{cos}\:\theta}{\mathrm{2}\:\mathrm{sin}\:\left(\beta−\theta\right)}=\frac{{Mg}}{\mathrm{2}\:\left(\mathrm{sin}\:\beta−\mathrm{cos}\:\beta\:\mathrm{tan}\:\theta\right)} \\ $$$${N}_{{B}} =\frac{{Mg}\:\mathrm{cos}\:\beta}{\mathrm{2}\:\mathrm{sin}\:\left(\beta−\theta\right)}=\frac{{Mg}}{\mathrm{2}\:\left(\mathrm{tan}\:\beta\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)} \\ $$$${horizontal}\:{component}\:{in}\:{rope}\:\mathrm{2}\:=\:{T}_{\mathrm{20}} \\ $$$${T}_{\mathrm{20}} ={T}_{{B}} \:\mathrm{cos}\:\beta=\frac{{Mg}}{\mathrm{2}\:\left(\mathrm{tan}\:\beta−\mathrm{tan}\:\theta\right)} \\ $$$${a}_{\mathrm{2}} =\frac{{T}_{\mathrm{20}} }{\rho_{\mathrm{2}} {g}}=\frac{{Ml}_{\mathrm{2}} }{\mathrm{2}\left(\mathrm{tan}\:\beta−\mathrm{tan}\:\theta\right){m}_{\mathrm{2}} } \\ $$$${eqn}.\:{of}\:{rope}\:\mathrm{2}: \\ $$$${y}={a}_{\mathrm{2}} \mathrm{cosh}\:\frac{{x}}{{a}_{\mathrm{2}} } \\ $$$${y}'=\mathrm{sinh}\:\frac{{x}}{{a}_{\mathrm{2}} } \\ $$$${s}={a}_{\mathrm{2}} \mathrm{sinh}\:\frac{{x}}{{a}_{\mathrm{2}} }\:\:\:\left({length}\:{of}\:{rope}\:{upon}\:{O}\right) \\ $$$${at}\:{B}: \\ $$$${y}_{{B}} ={a}_{\mathrm{2}} \mathrm{cosh}\:\frac{{e}_{\mathrm{2}} }{{a}_{\mathrm{2}} } \\ $$$${y}'_{{B}} =\mathrm{sinh}\:\frac{{e}_{\mathrm{2}} }{{a}_{\mathrm{2}} }=\mathrm{tan}\:\beta\:\Rightarrow\:\frac{{e}_{\mathrm{2}} }{{a}_{\mathrm{2}} }=\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right) \\ $$$${s}_{{B}} ={a}_{\mathrm{2}} \mathrm{sinh}\:\frac{{e}_{\mathrm{2}} }{{a}_{\mathrm{2}} }={a}_{\mathrm{2}} \mathrm{tan}\:\beta \\ $$$$\Rightarrow{y}_{{B}} ={a}_{\mathrm{2}} \mathrm{cosh}\:\frac{{e}_{\mathrm{2}} }{{a}_{\mathrm{2}} }={a}_{\mathrm{2}} \mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right)\right] \\ $$$${at}\:{C}: \\ $$$${y}_{{C}} ={a}_{\mathrm{2}} \mathrm{cosh}\:\frac{{e}_{\mathrm{2}} +{f}_{\mathrm{2}} }{{a}_{\mathrm{2}} }={a}_{\mathrm{2}} \mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right)+\frac{{f}_{\mathrm{2}} }{{a}_{\mathrm{2}} }\right] \\ $$$$={y}_{{B}} +{h}_{\mathrm{2}} ={a}_{\mathrm{2}} \mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right)\right]+{h}_{\mathrm{2}} \\ $$$$\Rightarrow{a}_{\mathrm{2}} \mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right)+\frac{{f}_{\mathrm{2}} }{{a}_{\mathrm{2}} }\right]−{a}_{\mathrm{2}} \mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right)\right]={h}_{\mathrm{2}} \\ $$$${s}_{{C}} ={a}_{\mathrm{2}} \mathrm{sinh}\:\frac{{e}_{\mathrm{2}} +{f}_{\mathrm{2}} }{{a}_{\mathrm{2}} }={a}_{\mathrm{2}} \mathrm{sinh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right)+\frac{{f}_{\mathrm{2}} }{{a}_{\mathrm{2}} }\right] \\ $$$$={s}_{{A}} +{l}_{\mathrm{2}} ={a}_{\mathrm{2}} \mathrm{tan}\:\beta+{l}_{\mathrm{2}} \\ $$$$…….\:{to}\:{be}\:{continued}\:…… \\ $$
Commented by mr W last updated on 29/Dec/18
![⇒sinh [sinh^(−1) (tan β)+(f_2 /a_2 )]=tan β+(l_2 /a_2 ) ⇒sinh^(−1) (tan β)+(f_2 /a_2 )=sinh^(−1) (tan β+(l_2 /a_2 )) ⇒(f_2 /a_2 )=sinh^(−1) (tan β+(l_2 /a_2 ))−sinh^(−1) (tan β) ⇒a_2 cosh [sinh^(−1) (tan β+(l_2 /a_2 ))]−a_2 cosh [sinh^(−1) (tan β)]=h_2 N_A =N_B : ⇒((Mg)/(2 (tan α cos θ+sin θ)))=((Mg)/(2 (tan β cos θ−sin θ))) ⇒tan α cos θ+sin θ=tan β cos θ−sin θ ⇒tan θ=((tan β−tan α)/2) ...(iii) ⇒a_1 =((Ml_1 )/((tan α+tan β)m_1 ))⇒(l_1 /a_1 )=(((tan α+tan β)m_1 )/M) ⇒a_2 =((Ml_2 )/((tan α+tan β)m_2 ))⇒(l_2 /a_2 )=(((tan α+tan β)m_2 )/M) f_1 +f_2 =b cos 𝛉: ⇒a_1 {sinh^(−1) (tan α+(l_1 /a_1 ))−sinh^(−1) (tan α)}+a_2 {sinh^(−1) (tan β+(l_2 /a_2 ))−sinh^(−1) (tan β)}=b cos θ ⇒((Ml_1 )/((tan α+tan β)m_1 b)){sinh^(−1) [(1+(m_1 /M))tan α+(m_1 /M) tan β]−sinh^(−1) (tan α)}+((Ml_2 )/((tan α+tan β)m_2 b)){sinh^(−1) ((m_2 /M) tan α+(1+(m_2 /M))tan β)−sinh^(−1) (tan β)}=(2/( (√(4+(tan β−tan α)^2 )))) ⇒((Ml_1 )/(m_1 b)){sinh^(−1) [(1+(m_1 /M))tan α+(m_1 /M) tan β]−sinh^(−1) (tan α)}+((Ml_2 )/(m_2 b)){sinh^(−1) ((m_2 /M) tan α+(1+(m_2 /M))tan β)−sinh^(−1) (tan β)}=((2 (tan β+tan α))/( (√(4+(tan β−tan α)^2 )))) h_2 −h_1 =b sin 𝛉: ⇒a_2 {cosh [sinh^(−1) (tan β+(l_2 /a_2 ))]−cosh [sinh^(−1) (tan β)]}−a_1 {cosh [sinh^(−1) (tan α+(l_1 /a_1 ))]−cosh [sinh^(−1) (tan α)]}=b sin θ ⇒((Ml_2 )/((tan α+tan β)m_2 b)){cosh [sinh^(−1) ((m_2 /M) tan α+(1+(m_2 /M))tan β)]−cosh [sinh^(−1) (tan β)]}−((Ml_1 )/((tan α+tan β)m_1 b)){cosh [sinh^(−1) ((1+(m_1 /M))tan α+(m_1 /M) tan β)]−cosh [sinh^(−1) (tan α)]}=((tan β−tan α)/( (√(4+(tan β−tan α)^2 )))) ⇒((Ml_2 )/(m_2 b)){cosh [sinh^(−1) ((m_2 /M) tan α+(1+(m_2 /M))tan β)]−cosh [sinh^(−1) (tan β)]}−((Ml_1 )/(m_1 b)){cosh [sinh^(−1) ((1+(m_1 /M))tan α+(m_1 /M) tan β)]−cosh [sinh^(−1) (tan α)]}=((tan^2 β−tan^2 α)/( (√(4+(tan β−tan α)^2 )))) with λ_1 =(l_1 /b), λ_2 =(l_2 /b), μ_1 =(m_1 /M), μ_2 =(m_2 /M) (𝛌_2 /𝛍_2 ){sinh^(−1) (𝛍_2 tan 𝛂+(1+𝛍_2 )tan 𝛃)−sinh^(−1) (tan 𝛃)}+(𝛌_1 /𝛍_1 ){sinh^(−1) [(1+𝛍_1 )tan 𝛂+𝛍_1 tan 𝛃]−sinh^(−1) (tan 𝛂)}=((2 (tan 𝛃+tan 𝛂))/( (√(4+(tan 𝛃−tan 𝛂)^2 )))) ...(i) (𝛌_2 /𝛍_2 ){cosh [sinh^(−1) (𝛍_2 tan 𝛂+(1+𝛍_2 )tan 𝛃)]−cosh [sinh^(−1) (tan 𝛃)]}−(𝛌_1 /𝛍_1 ){cosh [sinh^(−1) ((1+𝛍_1 )tan 𝛂+𝛍_1 tan 𝛃)]−cosh [sinh^(−1) (tan 𝛂)]}=((tan^2 𝛃−tan^2 𝛂)/( (√(4+(tan 𝛃−tan 𝛂)^2 )))) ...(ii) we obtain tan α and tan β from (i) and (ii), and then θ from (iii).](https://www.tinkutara.com/question/Q51601.png)
$$\Rightarrow\mathrm{sinh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right)+\frac{{f}_{\mathrm{2}} }{{a}_{\mathrm{2}} }\right]=\mathrm{tan}\:\beta+\frac{{l}_{\mathrm{2}} }{{a}_{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right)+\frac{{f}_{\mathrm{2}} }{{a}_{\mathrm{2}} }=\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta+\frac{{l}_{\mathrm{2}} }{{a}_{\mathrm{2}} }\right) \\ $$$$\Rightarrow\frac{{f}_{\mathrm{2}} }{{a}_{\mathrm{2}} }=\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta+\frac{{l}_{\mathrm{2}} }{{a}_{\mathrm{2}} }\right)−\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right) \\ $$$$\Rightarrow{a}_{\mathrm{2}} \mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta+\frac{{l}_{\mathrm{2}} }{{a}_{\mathrm{2}} }\right)\right]−{a}_{\mathrm{2}} \mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right)\right]={h}_{\mathrm{2}} \\ $$$$ \\ $$$$\boldsymbol{{N}}_{\boldsymbol{{A}}} =\boldsymbol{{N}}_{\boldsymbol{{B}}} : \\ $$$$\Rightarrow\frac{{Mg}}{\mathrm{2}\:\left(\mathrm{tan}\:\alpha\:\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)}=\frac{{Mg}}{\mathrm{2}\:\left(\mathrm{tan}\:\beta\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha\:\mathrm{cos}\:\theta+\mathrm{sin}\:\theta=\mathrm{tan}\:\beta\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{tan}\:\beta−\mathrm{tan}\:\alpha}{\mathrm{2}}\:\:\:\:…\left({iii}\right) \\ $$$$\Rightarrow{a}_{\mathrm{1}} =\frac{{Ml}_{\mathrm{1}} }{\left(\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta\right){m}_{\mathrm{1}} }\Rightarrow\frac{{l}_{\mathrm{1}} }{{a}_{\mathrm{1}} }=\frac{\left(\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta\right){m}_{\mathrm{1}} }{{M}} \\ $$$$\Rightarrow{a}_{\mathrm{2}} =\frac{{Ml}_{\mathrm{2}} }{\left(\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta\right){m}_{\mathrm{2}} }\Rightarrow\frac{{l}_{\mathrm{2}} }{{a}_{\mathrm{2}} }=\frac{\left(\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta\right){m}_{\mathrm{2}} }{{M}} \\ $$$$\boldsymbol{{f}}_{\mathrm{1}} +\boldsymbol{{f}}_{\mathrm{2}} =\boldsymbol{{b}}\:\boldsymbol{\mathrm{cos}}\:\boldsymbol{\theta}: \\ $$$$\Rightarrow{a}_{\mathrm{1}} \left\{\mathrm{sinh}^{−\mathrm{1}} \:\:\left(\mathrm{tan}\:\alpha+\frac{{l}_{\mathrm{1}} }{{a}_{\mathrm{1}} }\right)−\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)\right\}+{a}_{\mathrm{2}} \left\{\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta+\frac{{l}_{\mathrm{2}} }{{a}_{\mathrm{2}} }\right)−\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right)\right\}={b}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\frac{{Ml}_{\mathrm{1}} }{\left(\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta\right){m}_{\mathrm{1}} {b}}\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left[\left(\mathrm{1}+\frac{{m}_{\mathrm{1}} }{{M}}\right)\mathrm{tan}\:\alpha+\frac{{m}_{\mathrm{1}} }{{M}}\:\mathrm{tan}\:\beta\right]−\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)\right\}+\frac{{Ml}_{\mathrm{2}} }{\left(\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta\right){m}_{\mathrm{2}} {b}}\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{{m}_{\mathrm{2}} }{{M}}\:\mathrm{tan}\:\alpha+\left(\mathrm{1}+\frac{{m}_{\mathrm{2}} }{{M}}\right)\mathrm{tan}\:\beta\right)−\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right)\right\}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}+\left(\mathrm{tan}\:\beta−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow\frac{{Ml}_{\mathrm{1}} }{{m}_{\mathrm{1}} {b}}\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left[\left(\mathrm{1}+\frac{{m}_{\mathrm{1}} }{{M}}\right)\mathrm{tan}\:\alpha+\frac{{m}_{\mathrm{1}} }{{M}}\:\mathrm{tan}\:\beta\right]−\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)\right\}+\frac{{Ml}_{\mathrm{2}} }{{m}_{\mathrm{2}} {b}}\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{{m}_{\mathrm{2}} }{{M}}\:\mathrm{tan}\:\alpha+\left(\mathrm{1}+\frac{{m}_{\mathrm{2}} }{{M}}\right)\mathrm{tan}\:\beta\right)−\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right)\right\}=\frac{\mathrm{2}\:\left(\mathrm{tan}\:\beta+\mathrm{tan}\:\alpha\right)}{\:\sqrt{\mathrm{4}+\left(\mathrm{tan}\:\beta−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }}\: \\ $$$$\boldsymbol{{h}}_{\mathrm{2}} −\boldsymbol{{h}}_{\mathrm{1}} =\boldsymbol{{b}}\:\boldsymbol{\mathrm{sin}}\:\boldsymbol{\theta}: \\ $$$$\Rightarrow{a}_{\mathrm{2}} \left\{\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta+\frac{{l}_{\mathrm{2}} }{{a}_{\mathrm{2}} }\right)\right]−\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right)\right]\right\}−{a}_{\mathrm{1}} \left\{\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha+\frac{{l}_{\mathrm{1}} }{{a}_{\mathrm{1}} }\right)\right]−\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)\right]\right\}={b}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\frac{{Ml}_{\mathrm{2}} }{\left(\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta\right){m}_{\mathrm{2}} {b}}\left\{\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{{m}_{\mathrm{2}} }{{M}}\:\mathrm{tan}\:\alpha+\left(\mathrm{1}+\frac{{m}_{\mathrm{2}} }{{M}}\right)\mathrm{tan}\:\beta\right)\right]−\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right)\right]\right\}−\frac{{Ml}_{\mathrm{1}} }{\left(\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta\right){m}_{\mathrm{1}} {b}}\left\{\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\left(\mathrm{1}+\frac{{m}_{\mathrm{1}} }{{M}}\right)\mathrm{tan}\:\alpha+\frac{{m}_{\mathrm{1}} }{{M}}\:\mathrm{tan}\:\beta\right)\right]−\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)\right]\right\}=\frac{\mathrm{tan}\:\beta−\mathrm{tan}\:\alpha}{\:\sqrt{\mathrm{4}+\left(\mathrm{tan}\:\beta−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow\frac{{Ml}_{\mathrm{2}} }{{m}_{\mathrm{2}} {b}}\left\{\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{{m}_{\mathrm{2}} }{{M}}\:\mathrm{tan}\:\alpha+\left(\mathrm{1}+\frac{{m}_{\mathrm{2}} }{{M}}\right)\mathrm{tan}\:\beta\right)\right]−\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\beta\right)\right]\right\}−\frac{{Ml}_{\mathrm{1}} }{{m}_{\mathrm{1}} {b}}\left\{\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\left(\mathrm{1}+\frac{{m}_{\mathrm{1}} }{{M}}\right)\mathrm{tan}\:\alpha+\frac{{m}_{\mathrm{1}} }{{M}}\:\mathrm{tan}\:\beta\right)\right]−\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)\right]\right\}=\frac{\mathrm{tan}^{\mathrm{2}} \:\beta−\mathrm{tan}^{\mathrm{2}} \:\alpha}{\:\sqrt{\mathrm{4}+\left(\mathrm{tan}\:\beta−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }} \\ $$$${with}\:\lambda_{\mathrm{1}} =\frac{{l}_{\mathrm{1}} }{{b}},\:\lambda_{\mathrm{2}} =\frac{{l}_{\mathrm{2}} }{{b}},\:\mu_{\mathrm{1}} =\frac{{m}_{\mathrm{1}} }{{M}},\:\mu_{\mathrm{2}} =\frac{{m}_{\mathrm{2}} }{{M}} \\ $$$$\frac{\boldsymbol{\lambda}_{\mathrm{2}} }{\boldsymbol{\mu}_{\mathrm{2}} }\left\{\boldsymbol{\mathrm{sinh}}^{−\mathrm{1}} \left(\boldsymbol{\mu}_{\mathrm{2}} \boldsymbol{\mathrm{tan}}\:\boldsymbol{\alpha}+\left(\mathrm{1}+\boldsymbol{\mu}_{\mathrm{2}} \right)\boldsymbol{\mathrm{tan}}\:\boldsymbol{\beta}\right)−\boldsymbol{\mathrm{sinh}}^{−\mathrm{1}} \left(\boldsymbol{\mathrm{tan}}\:\boldsymbol{\beta}\right)\right\}+\frac{\boldsymbol{\lambda}_{\mathrm{1}} }{\boldsymbol{\mu}_{\mathrm{1}} }\left\{\boldsymbol{\mathrm{sinh}}^{−\mathrm{1}} \left[\left(\mathrm{1}+\boldsymbol{\mu}_{\mathrm{1}} \right)\boldsymbol{\mathrm{tan}}\:\boldsymbol{\alpha}+\boldsymbol{\mu}_{\mathrm{1}} \boldsymbol{\mathrm{tan}}\:\boldsymbol{\beta}\right]−\boldsymbol{\mathrm{sinh}}^{−\mathrm{1}} \left(\boldsymbol{\mathrm{tan}}\:\boldsymbol{\alpha}\right)\right\}=\frac{\mathrm{2}\:\left(\boldsymbol{\mathrm{tan}}\:\boldsymbol{\beta}+\boldsymbol{\mathrm{tan}}\:\boldsymbol{\alpha}\right)}{\:\sqrt{\mathrm{4}+\left(\boldsymbol{\mathrm{tan}}\:\boldsymbol{\beta}−\boldsymbol{\mathrm{tan}}\:\boldsymbol{\alpha}\right)^{\mathrm{2}} }}\:\:\:\:\:…\left({i}\right) \\ $$$$\frac{\boldsymbol{\lambda}_{\mathrm{2}} }{\boldsymbol{\mu}_{\mathrm{2}} }\left\{\boldsymbol{\mathrm{cosh}}\:\left[\boldsymbol{\mathrm{sinh}}^{−\mathrm{1}} \left(\boldsymbol{\mu}_{\mathrm{2}} \boldsymbol{\mathrm{tan}}\:\boldsymbol{\alpha}+\left(\mathrm{1}+\boldsymbol{\mu}_{\mathrm{2}} \right)\boldsymbol{\mathrm{tan}}\:\boldsymbol{\beta}\right)\right]−\boldsymbol{\mathrm{cosh}}\:\left[\boldsymbol{\mathrm{sinh}}^{−\mathrm{1}} \left(\boldsymbol{\mathrm{tan}}\:\boldsymbol{\beta}\right)\right]\right\}−\frac{\boldsymbol{\lambda}_{\mathrm{1}} }{\boldsymbol{\mu}_{\mathrm{1}} }\left\{\boldsymbol{\mathrm{cosh}}\:\left[\boldsymbol{\mathrm{sinh}}^{−\mathrm{1}} \left(\left(\mathrm{1}+\boldsymbol{\mu}_{\mathrm{1}} \right)\boldsymbol{\mathrm{tan}}\:\boldsymbol{\alpha}+\boldsymbol{\mu}_{\mathrm{1}} \boldsymbol{\mathrm{tan}}\:\boldsymbol{\beta}\right)\right]−\boldsymbol{\mathrm{cosh}}\:\left[\boldsymbol{\mathrm{sinh}}^{−\mathrm{1}} \left(\boldsymbol{\mathrm{tan}}\:\boldsymbol{\alpha}\right)\right]\right\}=\frac{\boldsymbol{\mathrm{tan}}^{\mathrm{2}} \:\boldsymbol{\beta}−\boldsymbol{\mathrm{tan}}^{\mathrm{2}} \:\boldsymbol{\alpha}}{\:\sqrt{\mathrm{4}+\left(\boldsymbol{\mathrm{tan}}\:\boldsymbol{\beta}−\boldsymbol{\mathrm{tan}}\:\boldsymbol{\alpha}\right)^{\mathrm{2}} }}\:\:\:\:\:…\left({ii}\right) \\ $$$${we}\:{obtain}\:\mathrm{tan}\:\alpha\:{and}\:\mathrm{tan}\:\beta\:{from}\:\left({i}\right)\:{and}\:\left({ii}\right), \\ $$$${and}\:{then}\:\theta\:{from}\:\left({iii}\right). \\ $$
Commented by ajfour last updated on 29/Dec/18
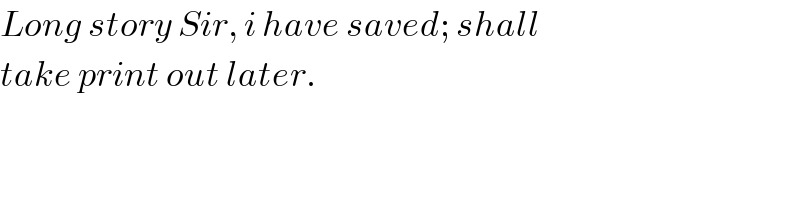
$${Long}\:{story}\:{Sir},\:{i}\:{have}\:{saved};\:{shall} \\ $$$${take}\:{print}\:{out}\:{later}. \\ $$
Commented by mr W last updated on 29/Dec/18
$${thanks}\:{for}\:{viewing}\:{sir}! \\ $$$${i}'{m}\:{not}\:{able}\:{to}\:{make}\:{the}\:{equations} \\ $$$${more}\:{simple}. \\ $$
