Question Number 51501 by Tinkutara last updated on 27/Dec/18

Answered by tanmay.chaudhury50@gmail.com last updated on 27/Dec/18
![x=tanθ dx=sec^2 θdθ ∫(θ/(tan^4 θ))sec^2 θdθ θ∫((sec^2 θ)/(tan^4 θ))dθ−∫[(dθ/dθ)∫((sec^2 θ)/(tan^4 θ))dθ]dθ =θ×((−1)/(3tan^3 θ))+(1/3)∫(dθ/(tan^3 θ)) now (1/3)∫(dθ/(tan^3 θ)) (1/3)∫(((1−sin^2 θ)cosθ)/(sin^3 θ))dθ (1/3)∫((1/(sin^3 θ))−(1/(sinθ)))d(sinθ) =(1/3)[(((sinθ)^(−3+1) )/(−3+1))−ln(sinθ)] answer is ((−θ)/(3tan^3 θ))+((−1)/6)×(1/(sin^2 θ))−(1/3)ln(sinθ)+c =((−tan^(−1) x)/(3x^3 ))+((−1)/6)×((1+x^2 )/x^2 )−(1/3)ln((x/( (√(1+x^2 )))))+c pls check [∫((sec^2 dθ)/(tan^4 θ))=(((tanθ)^(−4+1) )/(−4+1))+c]](https://www.tinkutara.com/question/Q51506.png)
$${x}={tan}\theta\:\:{dx}={sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$\int\frac{\theta}{{tan}^{\mathrm{4}} \theta}{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$\theta\int\frac{{sec}^{\mathrm{2}} \theta}{{tan}^{\mathrm{4}} \theta}{d}\theta−\int\left[\frac{{d}\theta}{{d}\theta}\int\frac{{sec}^{\mathrm{2}} \theta}{{tan}^{\mathrm{4}} \theta}{d}\theta\right]{d}\theta \\ $$$$=\theta×\frac{−\mathrm{1}}{\mathrm{3}{tan}^{\mathrm{3}} \theta}+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{d}\theta}{{tan}^{\mathrm{3}} \theta} \\ $$$${now}\:\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{d}\theta}{{tan}^{\mathrm{3}} \theta} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\left(\mathrm{1}−{sin}^{\mathrm{2}} \theta\right){cos}\theta}{{sin}^{\mathrm{3}} \theta}{d}\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\left(\frac{\mathrm{1}}{{sin}^{\mathrm{3}} \theta}−\frac{\mathrm{1}}{{sin}\theta}\right){d}\left({sin}\theta\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\left({sin}\theta\right)^{−\mathrm{3}+\mathrm{1}} }{−\mathrm{3}+\mathrm{1}}−{ln}\left({sin}\theta\right)\right] \\ $$$${answer}\:{is} \\ $$$$\frac{−\theta}{\mathrm{3}{tan}^{\mathrm{3}} \theta}+\frac{−\mathrm{1}}{\mathrm{6}}×\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \theta}−\frac{\mathrm{1}}{\mathrm{3}}{ln}\left({sin}\theta\right)+{c} \\ $$$$=\frac{−{tan}^{−\mathrm{1}} {x}}{\mathrm{3}{x}^{\mathrm{3}} }+\frac{−\mathrm{1}}{\mathrm{6}}×\frac{\mathrm{1}+{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{3}}{ln}\left(\frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)+{c} \\ $$$${pls}\:{check} \\ $$$$ \\ $$$$\left[\int\frac{{sec}^{\mathrm{2}} {d}\theta}{{tan}^{\mathrm{4}} \theta}=\frac{\left({tan}\theta\right)^{−\mathrm{4}+\mathrm{1}} }{−\mathrm{4}+\mathrm{1}}+{c}\right] \\ $$
Commented by Tinkutara last updated on 27/Dec/18
Thank you very much Sir! I got the answer. ��������
Commented by Tinkutara last updated on 27/Dec/18
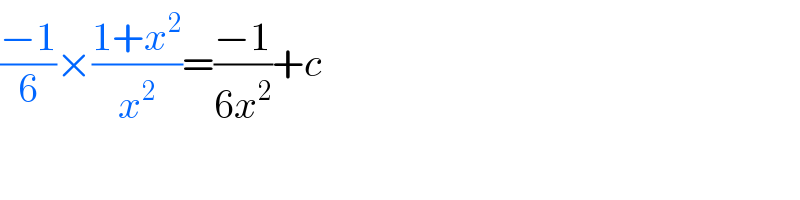
$$\frac{−\mathrm{1}}{\mathrm{6}}×\frac{\mathrm{1}+{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }=\frac{−\mathrm{1}}{\mathrm{6}{x}^{\mathrm{2}} }+{c} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Dec/18

$${most}\:{welcome}… \\ $$
