Menu Close

Question-51510

Tinku Tara 0 Comments
Pin




Question Number 51510 by Tinkutara last updated on 27/Dec/18
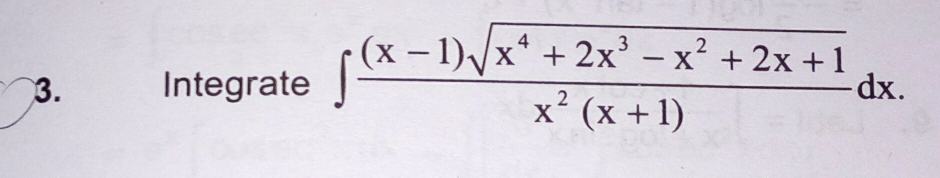
Answered by tanmay.chaudhury50@gmail.com last updated on 28/Dec/18
∫((−2pdp)/( (√(p^2 ×({1−3(p^2 −1)})))) x^2 {x^2 +(1/x^2 )+2(x+(1/x))−1} x^2 {(x+(1/x))^2 −2+2(x+(1/x))−1} x^2 {(x+(1/x))^2 +2(x+(1/x))−3} now ∫(((x−1)x(√({(x+(1/x))^2 +2(x+(1/x))−3))[)/(x^2 (x+1)))dx ∫(((x−1)(√({(x+(1/x))^2 +2(x+(1/x))−3))[)/(x^2 +x))dx ∫(((x^2 −1)(√({(x+(1/x))^2 +2(x+(1/x))−3)) )/(x(x+1)^2 ))dx ∫(((x^2 −1)(√({(x+(1/x))^2 +2(x+(1/x))−3)))/(x(x^2 +2x+1)))dx ∫(((1−(1/x^2 ))(√({(x+(1/x))^2 +2(x+(1/x))−3)))/((x+(1/x)+2)))dx put k=x+(1/x) dk=(1−(1/x^2 ))dx ∫((√(k^2 +2k−3))/(k+2)) dk wait i am near solution... ∫((k(k+2)−3)/((k+2)(√(k^2 +2k−3)) ))dk ∫(k/( (√(k^2 +2k−3))))dk−3∫(dk/((k+2)(√(k^2 +2k−3)))) ∫((k+1−1)/( (√(k^2 +2k−3))))dk−3∫(dk/((k+2)(√((k^2 +2k−3))))) (1/2)∫((d(k^2 +2k−3))/( (√(k^2 +2k−3))))−∫(dk/( (√((k+1)^2 −2^2 ))))−3∫(dk/((k+2)(√(k^2 +2k−3)))) I=(1/2)I_1 −I_2 −3I_3 I_1 =(((k^2 +2k−3)^(((−1)/2)+1) )/(((−1)/2)+1))=2(k^2 +2k−3)^(1/2) I_2 =∫(dk/( (√((k+1)^2 −2^2 ))))=ln{(k+1)+(√((k+1)^2 −2^2 )) } I_2 =ln{(k+1)+(√(k^2 +2k−3)) } I_3 =∫(dk/((k+2)(√(k^2 +2k−3))))→∫(dk/((k+2)(√((k+3)(k−1))))) k+2=(1/t) dk=((−1)/t^2 )dt ∫(((−1)/t^2 )/((1/t)(√(((1/t)+1)((1/t)−3)))))dt ∫(((−1)/t)/( (√((1+t)(1−3t))) ))×tdt =∫((−dt)/( (√((1+t)(1−3t))))) =∫((−dt)/( (√(1−2t−3t^2 )))) calculation −3t^2 −2t+1 =−3(t^2 +((2t)/3)+(1/(9 ))−(1/9)−(1/3)) =−3{(t+(1/3))^2 −((2/3))^2 }=3{((2/3))^2 −(t+(1/3))^2 } ∫((−dt)/( (√(3{((2/3))^2 −(t+(1/3))^2 })))) =((−1)/( (√3)))sin^(−1) (((t+(1/3))/(2/3)))=((−1)/( (√3)))sin^(−1) (((3t+1)/2))=((−1)/( (√3)))sin^(−1) (((3((1/(k+2)))+1)/2)) =((−1)/( (√3)))sin^(−1) (((k+5)/(2k+4))) so answer is (1/2)×2(k^2 +2k−3)^(1/2) −ln{(k+1)+(√(k^2 +2k−3)) )}−3×(((−1)/( (√3))))sin^(−1) (((k+5)/(2k+4))) =(k^2 +2k−3)^(1/2) −ln{(k+1)+(√(k^2 +2k−3)) )}+(√3) sin^(−1) (((k+5)/(2k+4)))
$$\int\frac{−\mathrm{2}{pdp}}{\:\sqrt{{p}^{\mathrm{2}} ×\left(\left\{\mathrm{1}−\mathrm{3}\left({p}^{\mathrm{2}} −\mathrm{1}\right)\right\}\right.}} \\ $$$${x}^{\mathrm{2}} \left\{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{1}\right\} \\ $$$${x}^{\mathrm{2}} \left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}+\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{1}\right\} \\ $$$${x}^{\mathrm{2}} \left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{3}\right\} \\ $$$${now} \\ $$$$\int\frac{\left({x}−\mathrm{1}\right){x}\sqrt{\left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{3}\right.}\left[\right.}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}{dx} \\ $$$$\int\frac{\left({x}−\mathrm{1}\right)\sqrt{\left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{3}\right.}\left[\right.}{{x}^{\mathrm{2}} +{x}}{dx} \\ $$$$\int\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{3}\right.}\:}{{x}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\int\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{3}\right.}}{{x}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\right)}{dx} \\ $$$$\int\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\sqrt{\left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{3}\right.}}{\left({x}+\frac{\mathrm{1}}{{x}}+\mathrm{2}\right)}{dx} \\ $$$${put}\:{k}={x}+\frac{\mathrm{1}}{{x}}\:\:\:{dk}=\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){dx} \\ $$$$\int\frac{\sqrt{{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}}}{{k}+\mathrm{2}}\:{dk} \\ $$$${wait}\:\:{i}\:{am}\:{near}\:{solution}… \\ $$$$\int\frac{{k}\left({k}+\mathrm{2}\right)−\mathrm{3}}{\left({k}+\mathrm{2}\right)\sqrt{{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}}\:}{dk} \\ $$$$\int\frac{{k}}{\:\sqrt{{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}}}{dk}−\mathrm{3}\int\frac{{dk}}{\left({k}+\mathrm{2}\right)\sqrt{{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}}} \\ $$$$\int\frac{{k}+\mathrm{1}−\mathrm{1}}{\:\sqrt{{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}}}{dk}−\mathrm{3}\int\frac{{dk}}{\left({k}+\mathrm{2}\right)\sqrt{\left({k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}\right)}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}\right)}{\:\sqrt{{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}}}−\int\frac{{dk}}{\:\sqrt{\left({k}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }}−\mathrm{3}\int\frac{{dk}}{\left({k}+\mathrm{2}\right)\sqrt{{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}}} \\ $$$$\boldsymbol{{I}}=\frac{\mathrm{1}}{\mathrm{2}}{I}_{\mathrm{1}} −{I}_{\mathrm{2}} −\mathrm{3}{I}_{\mathrm{3}} \\ $$$${I}_{\mathrm{1}} =\frac{\left({k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{1}} }{\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{1}}=\mathrm{2}\left({k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$ \\ $$$${I}_{\mathrm{2}} =\int\frac{{dk}}{\:\sqrt{\left({k}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }}={ln}\left\{\left({k}+\mathrm{1}\right)+\sqrt{\left({k}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }\:\right\} \\ $$$$\boldsymbol{{I}}_{\mathrm{2}} ={ln}\left\{\left({k}+\mathrm{1}\right)+\sqrt{{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}}\:\right\} \\ $$$${I}_{\mathrm{3}} =\int\frac{{dk}}{\left({k}+\mathrm{2}\right)\sqrt{{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}}}\rightarrow\int\frac{{dk}}{\left({k}+\mathrm{2}\right)\sqrt{\left({k}+\mathrm{3}\right)\left({k}−\mathrm{1}\right)}} \\ $$$${k}+\mathrm{2}=\frac{\mathrm{1}}{{t}}\:\:\boldsymbol{{dk}}=\frac{−\mathrm{1}}{\boldsymbol{{t}}^{\mathrm{2}} }\boldsymbol{{dt}} \\ $$$$\int\frac{\frac{−\mathrm{1}}{{t}^{\mathrm{2}} }}{\frac{\mathrm{1}}{{t}}\sqrt{\left(\frac{\mathrm{1}}{{t}}+\mathrm{1}\right)\left(\frac{\mathrm{1}}{{t}}−\mathrm{3}\right)}}{dt} \\ $$$$\int\frac{\frac{−\mathrm{1}}{{t}}}{\:\sqrt{\left(\mathrm{1}+{t}\right)\left(\mathrm{1}−\mathrm{3}{t}\right)}\:}×{tdt} \\ $$$$ \\ $$$$=\int\frac{−{dt}}{\:\sqrt{\left(\mathrm{1}+{t}\right)\left(\mathrm{1}−\mathrm{3}{t}\right)}}\:\:=\int\frac{−{dt}}{\:\sqrt{\mathrm{1}−\mathrm{2}{t}−\mathrm{3}{t}^{\mathrm{2}} }} \\ $$$${calculation} \\ $$$$−\mathrm{3}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1} \\ $$$$=−\mathrm{3}\left({t}^{\mathrm{2}} +\frac{\mathrm{2}{t}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{9}\:}−\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=−\mathrm{3}\left\{\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} \right\}=\mathrm{3}\left\{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} −\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} \right\} \\ $$$$\int\frac{−{dt}}{\:\sqrt{\mathrm{3}\left\{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} −\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} \right\}}} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}{sin}^{−\mathrm{1}} \left(\frac{{t}+\frac{\mathrm{1}}{\mathrm{3}}}{\frac{\mathrm{2}}{\mathrm{3}}}\right)=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}{t}+\mathrm{1}}{\mathrm{2}}\right)=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}\left(\frac{\mathrm{1}}{{k}+\mathrm{2}}\right)+\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}{sin}^{−\mathrm{1}} \left(\frac{{k}+\mathrm{5}}{\mathrm{2}{k}+\mathrm{4}}\right) \\ $$$$ \\ $$$$ \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{answer}}\:\boldsymbol{{is}} \\ $$$$\left.\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\left(\boldsymbol{{k}}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} −{ln}\left\{\left({k}+\mathrm{1}\right)+\sqrt{{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}}\:\right)\right\}−\mathrm{3}×\left(\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right){sin}^{−\mathrm{1}} \left(\frac{{k}+\mathrm{5}}{\mathrm{2}{k}+\mathrm{4}}\right) \\ $$$$\left.=\left(\boldsymbol{{k}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{k}}−\mathrm{3}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} −\boldsymbol{{ln}}\left\{\left(\boldsymbol{{k}}+\mathrm{1}\right)+\sqrt{\boldsymbol{{k}}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}}\:\right)\right\}+\sqrt{\mathrm{3}}\:{sin}^{−\mathrm{1}} \left(\frac{{k}+\mathrm{5}}{\mathrm{2}{k}+\mathrm{4}}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by Tinkutara last updated on 27/Dec/18
Commented by Tinkutara last updated on 28/Dec/18
Yes Sir, I am also getting the same answer as yours. There should be +√3 sin inverse…
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Dec/18
in white paper it can be solved quickly no need of typing.. i have solved the lengthy problem ∫(((√(k^2 +2k−3)) )/(k+2))dk ...pls check...
$$\boldsymbol{{in}}\:\boldsymbol{{white}}\:\boldsymbol{{paper}}\:\boldsymbol{{it}}\:\boldsymbol{{can}}\:\boldsymbol{{be}}\:\boldsymbol{{solved}}\:\:\boldsymbol{{quickly}} \\ $$$$\boldsymbol{{no}}\:\boldsymbol{{need}}\:\boldsymbol{{of}}\:\boldsymbol{{typing}}.. \\ $$$$\boldsymbol{{i}}\:\boldsymbol{{have}}\:\boldsymbol{{solved}}\:\boldsymbol{{the}}\:\boldsymbol{{lengthy}}\:\boldsymbol{{problem}} \\ $$$$\int\frac{\sqrt{{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}}\:}{{k}+\mathrm{2}}{dk}\:…{pls}\:{check}… \\ $$
Commented by Tinkutara last updated on 27/Dec/18
This is the answer given.
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Dec/18
pls check...final ansser...
$${pls}\:{check}…{final}\:{ansser}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *