Question Number 51535 by ajfour last updated on 28/Dec/18

Commented by ajfour last updated on 28/Dec/18
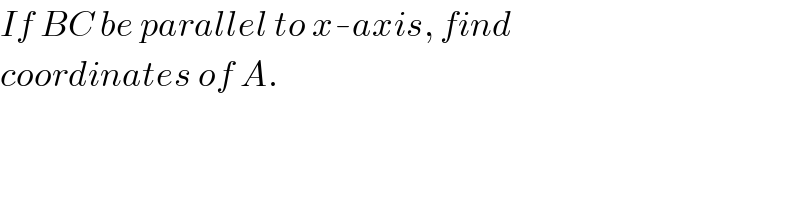
$${If}\:{BC}\:{be}\:{parallel}\:{to}\:{x}-{axis},\:{find} \\ $$$${coordinates}\:{of}\:{A}. \\ $$
Answered by mr W last updated on 28/Dec/18

$${B}\left(\frac{{a}}{\mathrm{2}},\:−\sqrt{{R}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}},\:\mathrm{0}\right) \\ $$$${C}\left(−\frac{{a}}{\mathrm{2}},\:−\sqrt{{R}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}},\:\mathrm{0}\right) \\ $$$${x}_{{A}} ^{\mathrm{2}} +{y}_{{A}} ^{\mathrm{2}} +{z}_{{A}} ^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$$\left({x}_{{A}} −\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}_{{A}} +\sqrt{{R}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}\right)^{\mathrm{2}} +{z}_{{A}} ^{\mathrm{2}} ={c}^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$$$\left({x}_{{A}} +\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}_{{A}} +\sqrt{{R}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}\right)^{\mathrm{2}} +{z}_{{A}} ^{\mathrm{2}} ={b}^{\mathrm{2}} \:\:\:…\left({iii}\right) \\ $$$$ \\ $$$$\left({iii}\right)−\left({ii}\right): \\ $$$$\mathrm{2}{ax}_{{A}} ={b}^{\mathrm{2}} −{c}^{\mathrm{2}} \\ $$$$\Rightarrow{x}_{{A}} =\frac{{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{a}} \\ $$$$\left({iii}\right)−\left({i}\right): \\ $$$$\sqrt{{R}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}\left(\mathrm{2}{y}_{{A}} +\sqrt{{R}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}\right)+\frac{{a}}{\mathrm{2}}\left(\mathrm{2}{x}_{{A}} +\frac{{a}}{\mathrm{2}}\right)={b}^{\mathrm{2}} −{R}^{\mathrm{2}} \\ $$$$\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }\left(\mathrm{4}{y}_{{A}} +\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }\right)=\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}{c}^{\mathrm{2}} −{a}^{\mathrm{2}} −\mathrm{4}{R}^{\mathrm{2}} \\ $$$$\mathrm{2}{y}_{{A}} \sqrt{\mathrm{4}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }={b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{4}{R}^{\mathrm{2}} \\ $$$$\Rightarrow{y}_{{A}} =\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{4}{R}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }} \\ $$$$\Rightarrow{z}_{{A}} =\sqrt{{R}^{\mathrm{2}} −{x}_{{A}} ^{\mathrm{2}} −{y}_{{A}} ^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 28/Dec/18

$${Beautiful}\:{expression}!\:{whats}\:{the} \\ $$$${logic}\:{sir}\:? \\ $$
Commented by ajfour last updated on 28/Dec/18

$${Wonderfully}\:\:{presented}\:{Sir}.\:{Thanks}. \\ $$$${Easy}\:{one}\:{for}\:{you},\:{i}\:{think}. \\ $$
Commented by mr W last updated on 28/Dec/18

$${thank}\:{you}\:{sir}! \\ $$$${a}\:{related}\:{question}\:{sir}: \\ $$$${which}\:{relation}\:{must}\:{the}\:{sides}\:{a},{b},{c} \\ $$$${have}\:{such}\:{that} \\ $$$${the}\:{triangle}\:{can}\:{be}\:{placed}\:{into}\:{a} \\ $$$${sphere}\:{with}\:{radius}\:{R}? \\ $$
Commented by mr W last updated on 28/Dec/18

$${i}\:{think}\:{the}\:{condition}\:{that}\:{the}\:{triangle} \\ $$$${can}\:{be}\:{placed}\:{into}\:{the}\:{sphere}\:{is} \\ $$$$\frac{{abc}}{\:\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}}\leqslant{R} \\ $$
Commented by mr W last updated on 28/Dec/18

$${the}\:{curcumcircle}\:{of}\:{the}\:{triangle}\:{must} \\ $$$${fit}\:{into}\:{the}\:{sphere},\:{i}.{e}.\:{the}\:{circumradius} \\ $$$${of}\:{the}\:{triangle}\:{must}\:{be}\:{less}\:{than}\:{or} \\ $$$${equal}\:{to}\:{the}\:{radius}\:{of}\:{the}\:{sphere}. \\ $$
