Question Number 51539 by ajfour last updated on 28/Dec/18
Commented by ajfour last updated on 28/Dec/18

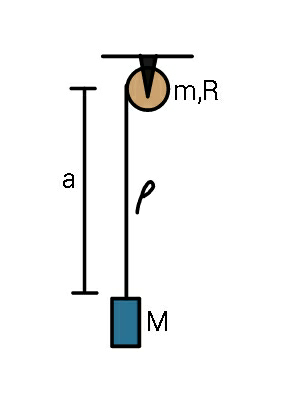
$${Rope}\:{has}\:{a}\:{total}\:{length}\:{L}\:{and}\:{linear} \\ $$$${mass}\:{density}\:\rho.\:{System}\:{is}\:{released} \\ $$$${as}\:{shown}.\:{The}\:{pulley}\:{is}\:{a}\:{disc}.\:{Find} \\ $$$${time}\:{it}\:{takes}\:{for}\:{the}\:{rope}\:{to}\:{unwind} \\ $$$${completely}. \\ $$
Answered by mr W last updated on 28/Dec/18
![let x=unwinded length of rope with x_0 =a T=tension in rope velocity v=(dx/dt), acceletation b=(dv/dt) m_1 =M+xρ (dm_1 /dt)=ρ(dx/dt)=ρv v_(rel) =−v m_1 g−T+v_(rel) (dm_1 /dt)=m_1 b (M+ρx)g−T−ρv^2 =(M+ρx)(dv/dt) ω=(v/R) α=(b/R)=(1/R)(dv/dt) m_2 =m+ρ(l−x)ρ I=(1/2)mR^2 +ρ(l−x)R^2 =[(m/2)+ρ(l−x)]R^2 (dI/dt)=−ρR^2 (dx/dt)=−ρR^2 v ((d(Iω))/dt)=TR I(dω/dt)+ω(dI/dt)=TR Iα−(v/R)×ρR^2 v=TR Iα−ρRv^2 =TR [(m/2)+ρ(l−x)]R^2 ×(1/R)(dv/dt)−ρRv^2 =TR T=[(m/2)+ρ(l−x)](dv/dt)−ρv^2 ⇒(M+ρx)g−[(m/2)+ρ(l−x)](dv/dt)+ρv^2 −ρv^2 =(M+ρx)(dv/dt) ⇒Mg+ρgx=(M+(m/2)+ρl)(dv/dt) (dv/dt)=(dv/dx)×(dx/dt)=v(dv/dx) ⇒v((M/ρ)+(m/(2ρ))+l)(dv/dx)=gx+(M/ρ)g let c=(M/ρ)+(m/(2ρ))+l, d=(M/ρ) ⇒cv(dv/dx)=g(x+d) c∫_0 ^v vdv=g∫_a ^x (x+d)dx ((cv^2 )/2)=g[(((x^2 −a^2 ))/2)+d(x−a)] ⇒v^2 =(g/c)(x+a+2d)(x−a) ⇒v=(dx/dt)=(√((g/c)(x+a+2d)(x−a))) (dx/( (√((x+a+2d)(x−a)))))=(√(g/c)) dt ∫_a ^l (dx/( (√((x+a+2d)(x−a)))))=t(√(g/c)) ∫_0 ^(l−a) (du/( (√(u{u+2(d+a)}))))=t(√(g/c)) 2[ln ((√(u+2(d+a)))+(√u))]_0 ^(l−a) =t(√(g/c)) 2[ln ((√(l−a+2(d+a)))+(√(l−a)))−ln ((√(2(d+a))))] =t(√(g/c)) t=(√(c/g))ln ((((√(l−a+2(d+a)))+(√(l−a)))^2 )/(2(d+a))) ⇒t=(√(c/g))ln ((l+d+(√((l−a)(l+a+2d))))/(a+d)) with c=(M/ρ)+(m/(2ρ))+l, d=(M/ρ)](https://www.tinkutara.com/question/Q51543.png)
$${let}\:{x}={unwinded}\:{length}\:{of}\:{rope}\:{with} \\ $$$${x}_{\mathrm{0}} ={a} \\ $$$${T}={tension}\:{in}\:{rope} \\ $$$${velocity}\:{v}=\frac{{dx}}{{dt}},\:{acceletation}\:{b}=\frac{{dv}}{{dt}} \\ $$$${m}_{\mathrm{1}} ={M}+{x}\rho \\ $$$$\frac{{dm}_{\mathrm{1}} }{{dt}}=\rho\frac{{dx}}{{dt}}=\rho{v} \\ $$$${v}_{{rel}} =−{v} \\ $$$${m}_{\mathrm{1}} {g}−{T}+{v}_{{rel}} \frac{{dm}_{\mathrm{1}} }{{dt}}={m}_{\mathrm{1}} {b} \\ $$$$\left({M}+\rho{x}\right){g}−{T}−\rho{v}^{\mathrm{2}} =\left({M}+\rho{x}\right)\frac{{dv}}{{dt}} \\ $$$$ \\ $$$$\omega=\frac{{v}}{{R}} \\ $$$$\alpha=\frac{{b}}{{R}}=\frac{\mathrm{1}}{{R}}\frac{{dv}}{{dt}} \\ $$$${m}_{\mathrm{2}} ={m}+\rho\left({l}−{x}\right)\rho \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}{mR}^{\mathrm{2}} +\rho\left({l}−{x}\right){R}^{\mathrm{2}} =\left[\frac{{m}}{\mathrm{2}}+\rho\left({l}−{x}\right)\right]{R}^{\mathrm{2}} \\ $$$$\frac{{dI}}{{dt}}=−\rho{R}^{\mathrm{2}} \frac{{dx}}{{dt}}=−\rho{R}^{\mathrm{2}} {v} \\ $$$$\frac{{d}\left({I}\omega\right)}{{dt}}={TR} \\ $$$${I}\frac{{d}\omega}{{dt}}+\omega\frac{{dI}}{{dt}}={TR} \\ $$$${I}\alpha−\frac{{v}}{{R}}×\rho{R}^{\mathrm{2}} {v}={TR} \\ $$$${I}\alpha−\rho{Rv}^{\mathrm{2}} ={TR} \\ $$$$\left[\frac{{m}}{\mathrm{2}}+\rho\left({l}−{x}\right)\right]{R}^{\mathrm{2}} ×\frac{\mathrm{1}}{{R}}\frac{{dv}}{{dt}}−\rho{Rv}^{\mathrm{2}} ={TR} \\ $$$${T}=\left[\frac{{m}}{\mathrm{2}}+\rho\left({l}−{x}\right)\right]\frac{{dv}}{{dt}}−\rho{v}^{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow\left({M}+\rho{x}\right){g}−\left[\frac{{m}}{\mathrm{2}}+\rho\left({l}−{x}\right)\right]\frac{{dv}}{{dt}}+\rho{v}^{\mathrm{2}} −\rho{v}^{\mathrm{2}} =\left({M}+\rho{x}\right)\frac{{dv}}{{dt}} \\ $$$$\Rightarrow{Mg}+\rho{gx}=\left({M}+\frac{{m}}{\mathrm{2}}+\rho{l}\right)\frac{{dv}}{{dt}} \\ $$$$\frac{{dv}}{{dt}}=\frac{{dv}}{{dx}}×\frac{{dx}}{{dt}}={v}\frac{{dv}}{{dx}} \\ $$$$\Rightarrow{v}\left(\frac{{M}}{\rho}+\frac{{m}}{\mathrm{2}\rho}+{l}\right)\frac{{dv}}{{dx}}={gx}+\frac{{M}}{\rho}{g} \\ $$$${let}\:{c}=\frac{{M}}{\rho}+\frac{{m}}{\mathrm{2}\rho}+{l},\:{d}=\frac{{M}}{\rho} \\ $$$$\Rightarrow{cv}\frac{{dv}}{{dx}}={g}\left({x}+{d}\right) \\ $$$${c}\int_{\mathrm{0}} ^{{v}} {vdv}={g}\int_{{a}} ^{{x}} \left({x}+{d}\right){dx} \\ $$$$\frac{{cv}^{\mathrm{2}} }{\mathrm{2}}={g}\left[\frac{\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}{\mathrm{2}}+{d}\left({x}−{a}\right)\right] \\ $$$$\Rightarrow{v}^{\mathrm{2}} =\frac{{g}}{{c}}\left({x}+{a}+\mathrm{2}{d}\right)\left({x}−{a}\right) \\ $$$$\Rightarrow{v}=\frac{{dx}}{{dt}}=\sqrt{\frac{{g}}{{c}}\left({x}+{a}+\mathrm{2}{d}\right)\left({x}−{a}\right)} \\ $$$$\frac{{dx}}{\:\sqrt{\left({x}+{a}+\mathrm{2}{d}\right)\left({x}−{a}\right)}}=\sqrt{\frac{{g}}{{c}}}\:{dt} \\ $$$$\int_{{a}} ^{{l}} \frac{{dx}}{\:\sqrt{\left({x}+{a}+\mathrm{2}{d}\right)\left({x}−{a}\right)}}={t}\sqrt{\frac{{g}}{{c}}} \\ $$$$\int_{\mathrm{0}} ^{{l}−{a}} \frac{{du}}{\:\sqrt{{u}\left\{{u}+\mathrm{2}\left({d}+{a}\right)\right\}}}={t}\sqrt{\frac{{g}}{{c}}} \\ $$$$\mathrm{2}\left[\mathrm{ln}\:\left(\sqrt{{u}+\mathrm{2}\left({d}+{a}\right)}+\sqrt{{u}}\right)\right]_{\mathrm{0}} ^{{l}−{a}} \:={t}\sqrt{\frac{{g}}{{c}}} \\ $$$$\mathrm{2}\left[\mathrm{ln}\:\left(\sqrt{{l}−{a}+\mathrm{2}\left({d}+{a}\right)}+\sqrt{{l}−{a}}\right)−\mathrm{ln}\:\left(\sqrt{\mathrm{2}\left({d}+{a}\right)}\right)\right]\:={t}\sqrt{\frac{{g}}{{c}}} \\ $$$${t}=\sqrt{\frac{{c}}{{g}}}\mathrm{ln}\:\frac{\left(\sqrt{{l}−{a}+\mathrm{2}\left({d}+{a}\right)}+\sqrt{{l}−{a}}\right)^{\mathrm{2}} }{\mathrm{2}\left({d}+{a}\right)} \\ $$$$\Rightarrow{t}=\sqrt{\frac{{c}}{{g}}}\mathrm{ln}\:\frac{{l}+{d}+\sqrt{\left({l}−{a}\right)\left({l}+{a}+\mathrm{2}{d}\right)}}{{a}+{d}} \\ $$$${with}\:{c}=\frac{{M}}{\rho}+\frac{{m}}{\mathrm{2}\rho}+{l},\:{d}=\frac{{M}}{\rho} \\ $$
Commented by ajfour last updated on 29/Dec/18
$${Thanks}\:{for}\:{the}\:{dynamic}\:{way}\:{Sir}! \\ $$
Answered by ajfour last updated on 28/Dec/18
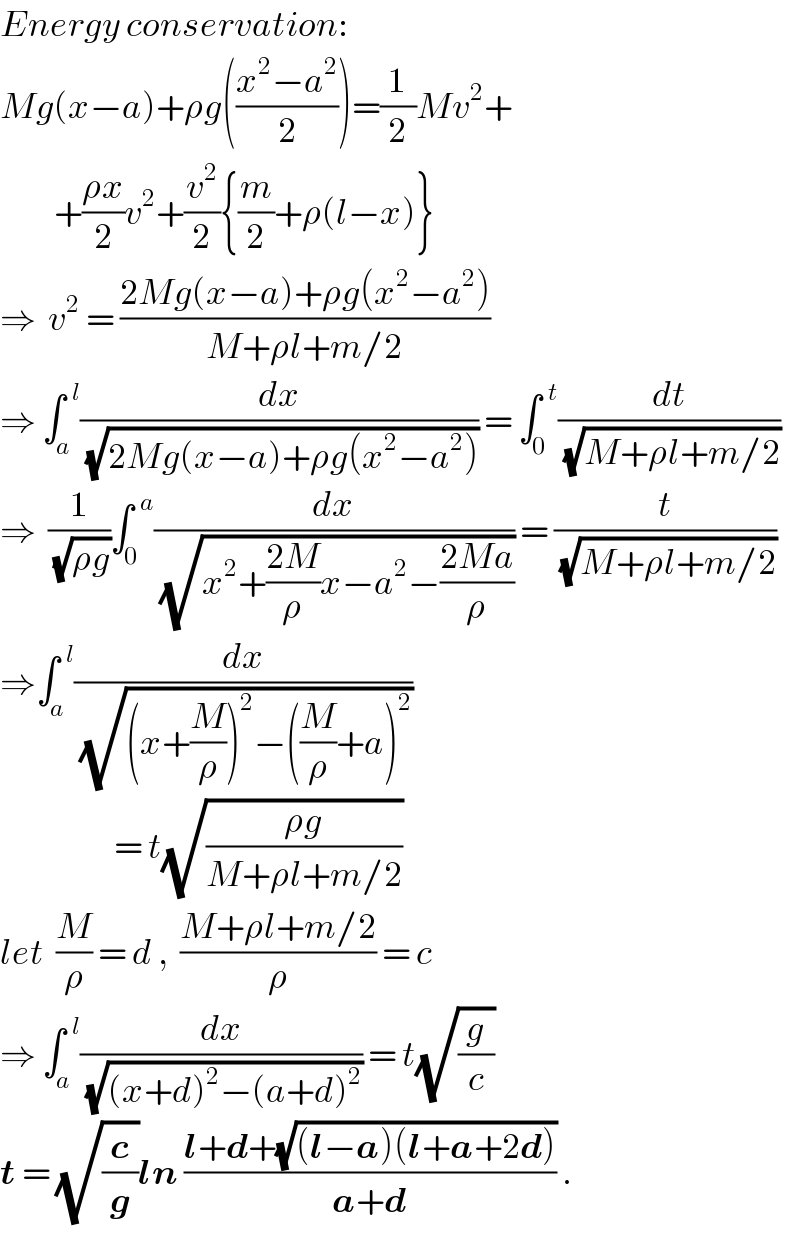
$${Energy}\:{conservation}: \\ $$$${Mg}\left({x}−{a}\right)+\rho{g}\left(\frac{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}{Mv}^{\mathrm{2}} + \\ $$$$\:\:\:\:\:\:\:\:\:+\frac{\rho{x}}{\mathrm{2}}{v}^{\mathrm{2}} +\frac{{v}^{\mathrm{2}} }{\mathrm{2}}\left\{\frac{{m}}{\mathrm{2}}+\rho\left({l}−{x}\right)\right\} \\ $$$$\Rightarrow\:\:{v}^{\mathrm{2}} \:=\:\frac{\mathrm{2}{Mg}\left({x}−{a}\right)+\rho{g}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}{{M}+\rho{l}+{m}/\mathrm{2}} \\ $$$$\Rightarrow\:\int_{{a}} ^{\:\:{l}} \frac{{dx}}{\:\sqrt{\mathrm{2}{Mg}\left({x}−{a}\right)+\rho{g}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}}\:=\:\int_{\mathrm{0}} ^{\:\:{t}} \frac{{dt}}{\:\sqrt{{M}+\rho{l}+{m}/\mathrm{2}}} \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{\:\sqrt{\rho{g}}}\int_{\mathrm{0}} ^{\:\:{a}} \frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +\frac{\mathrm{2}{M}}{\rho}{x}−{a}^{\mathrm{2}} −\frac{\mathrm{2}{Ma}}{\rho}}}\:=\:\frac{{t}}{\:\sqrt{{M}+\rho{l}+{m}/\mathrm{2}}} \\ $$$$\Rightarrow\int_{{a}} ^{\:\:{l}} \frac{{dx}}{\:\sqrt{\left({x}+\frac{{M}}{\rho}\right)^{\mathrm{2}} −\left(\frac{{M}}{\rho}+{a}\right)^{\mathrm{2}} }}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{t}\sqrt{\frac{\rho{g}}{{M}+\rho{l}+{m}/\mathrm{2}}} \\ $$$${let}\:\:\frac{{M}}{\rho}\:=\:{d}\:,\:\:\frac{{M}+\rho{l}+{m}/\mathrm{2}}{\rho}\:=\:{c} \\ $$$$\Rightarrow\:\int_{{a}} ^{\:\:{l}} \frac{{dx}}{\:\sqrt{\left({x}+{d}\right)^{\mathrm{2}} −\left({a}+{d}\right)^{\mathrm{2}} }}\:=\:{t}\sqrt{\frac{{g}}{{c}}} \\ $$$$\boldsymbol{{t}}\:=\:\sqrt{\frac{\boldsymbol{{c}}}{\boldsymbol{{g}}}}\boldsymbol{{ln}}\:\frac{\boldsymbol{{l}}+\boldsymbol{{d}}+\sqrt{\left(\boldsymbol{{l}}−\boldsymbol{{a}}\right)\left(\boldsymbol{{l}}+\boldsymbol{{a}}+\mathrm{2}\boldsymbol{{d}}\right)}}{\boldsymbol{{a}}+\boldsymbol{{d}}}\:. \\ $$
Commented by ajfour last updated on 28/Dec/18
$${thanks}\:{for}\:{checking}\:{Sir}. \\ $$
Commented by mr W last updated on 28/Dec/18
$${we}\:{have}\:{the}\:{same}\:{result}. \\ $$
